20 câu hỏi
Nghiệm của phương trình \[{\rm{cosx = cos}}\frac{{\rm{\pi }}}{{{\rm{12}}}}\]là
\(\left[ {\begin{array}{*{20}{c}}{{\rm{x = }}\frac{{\rm{\pi }}}{{{\rm{12}}}}{\rm{ + k2\pi }}}\\{{\rm{x = }}\frac{{{\rm{11\pi }}}}{{{\rm{12}}}}{\rm{ + }}l{\rm{2\pi }}}\end{array}} \right.\left( {k,l \in \mathbb{Z}} \right)\)
\(\left[ {\begin{array}{*{20}{c}}{{\rm{x = }}\frac{{\rm{\pi }}}{{{\rm{12}}}}{\rm{ + k2\pi }}}\\{{\rm{x = }} - \frac{{\rm{\pi }}}{{{\rm{12}}}}{\rm{ + k2\pi }}}\end{array}} \right.\left( {k \in \mathbb{Z}} \right)\)
\({\rm{x = }}\frac{{\rm{\pi }}}{{{\rm{12}}}}{\rm{ + k2\pi }}\left( {k \in \mathbb{Z}} \right)\)
\({\rm{x = }}\frac{{{\rm{11\pi }}}}{{{\rm{12}}}}{\rm{ + k2\pi }}\,\left( {k \in \mathbb{Z}} \right)\)
Giải phương trình \[\sqrt {\rm{3}} {\rm{tan2x}} - {\rm{3 = 0}}\]
\[{\rm{x = }}\frac{{\rm{\pi }}}{{\rm{6}}}{\rm{ + k\pi }}\,\,\left( {{\rm{k}} \in \mathbb{Z}} \right)\]
\[{\rm{x = }}\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k}}\frac{{\rm{\pi }}}{{\rm{2}}}\,\,\left( {{\rm{k}} \in \mathbb{Z}} \right)\]
\[{\rm{x = }}\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k\pi }}\,\,\left( {{\rm{k}} \in \mathbb{Z}} \right)\]
\[{\rm{x = }}\frac{{\rm{\pi }}}{{\rm{6}}}{\rm{ + k}}\frac{{\rm{\pi }}}{{\rm{2}}}\,\,\left( {{\rm{k}} \in \mathbb{Z}} \right)\]
Tìm nghiệm của phương trình \[{\rm{2sinx}} - {\rm{3 = 0}}\]
\[{\rm{x}} \in \emptyset \]
\(\left[ {\begin{array}{*{20}{c}}{{\rm{x = arcsin}}\left( {\frac{{\rm{3}}}{{\rm{2}}}} \right){\rm{ + k2\pi }}}\\{{\rm{x = \pi }} - {\rm{arcsin}}\left( {\frac{{\rm{3}}}{{\rm{2}}}} \right){\rm{ + k2\pi }}}\end{array}} \right.\left( {k \in \mathbb{Z}} \right)\)
\(\left[ {\begin{array}{*{20}{c}}{{\rm{x = arcsin}}\left( {\frac{{\rm{3}}}{{\rm{2}}}} \right){\rm{ + k2\pi }}}\\{{\rm{x = }} - {\rm{arcsin}}\left( {\frac{{\rm{3}}}{{\rm{2}}}} \right){\rm{ + k2\pi }}}\end{array}} \right.\left( {k \in \mathbb{Z}} \right)\)
\(x \in \mathbb{R}\)
Tìm số nghiệm thuộc đoạn\[\left[ {{\rm{\pi ; 2\pi }}} \right]\]của phương trình\[{\rm{sin}}\left( {{\rm{x + }}\frac{{\rm{\pi }}}{{\rm{4}}}} \right){\rm{ = 1}}\]
0
1
2
3
Gọi nghiệm lớn nhất trên khoảng\[\left( {{\rm{0; \pi }}} \right)\] của phương trình \[{\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm{x + co}}{{\rm{s}}^{\rm{2}}}{\rm{4x = 1}}\]có dạng\[{{\rm{x}}_{\rm{0}}}{\rm{ = }}\frac{{{\rm{\pi a}}}}{{\rm{b}}}\]. Tính giá trị biểu thức\[{\rm{P = }}{{\rm{a}}^{\rm{2}}}{\rm{ + }}{{\rm{b}}^{\rm{2}}}\]
29
41
34
13
Tìm tập nghiệm của phương trình \[{\rm{tan3x + tanx = 0}}\]
\[\left\{ {\frac{{\rm{\pi }}}{{\rm{4}}}{\rm{ + }}\frac{{{\rm{k\pi }}}}{{\rm{2}}}} \right\}\]
\[\left\{ {\frac{{{\rm{k\pi }}}}{{\rm{4}}}} \right\}\]
\[\left\{ {{\rm{k\pi ; }}\frac{{\rm{\pi }}}{{\rm{4}}}{\rm{ + }}\frac{{{\rm{k\pi }}}}{{\rm{2}}}} \right\}\]
\[\left\{ {{\rm{k\pi ; }}\frac{{\rm{\pi }}}{{\rm{4}}}{\rm{ + k\pi }}} \right\}\]
Tính tổng S các nghiệm trên đoạn \[\left[ {{\rm{0; 2\pi }}} \right]\] của phương trình\[\frac{{{\rm{cos2x}}}}{{{\rm{1}} - {\rm{sin2x}}}}{\rm{ = 0}}\]
\[{\rm{S = }}\frac{{{\rm{3\pi }}}}{{\rm{2}}}\]
\[{\rm{S = }}\frac{{\rm{\pi }}}{{\rm{2}}}\]
\[{\rm{S = 4\pi }}\]
\[{\rm{S = }}\frac{{{\rm{5\pi }}}}{{\rm{2}}}\]
Tìm số nghiệm của phương trình \[\sqrt {{\rm{4}} - {{\rm{x}}^{\rm{2}}}} {\rm{sin2x = 0}}\]
4
5
3
6
Tất cả các nghiệm của phương trình \[{\mathop{\rm c}\nolimits} {\rm{os}}\left( {\frac{{{\rm{2\pi }}}}{{\rm{3}}}{\rm{sinx}} - \frac{{{\rm{2\pi }}}}{{\rm{3}}}} \right){\rm{ = 1}}\] có dạng
\[{{\rm{x}}_{\rm{0}}}{\rm{ = }}\frac{{\rm{\pi }}}{{\rm{m}}}{\rm{ + kn\pi ;}}\,\,{\rm{k, m, n}} \in \mathbb{Z}\]. Tính tổng\[{\rm{S = m + n}}\]
S = 4
S = 3
\[{\rm{S = }}\frac{{\rm{7}}}{{\rm{3}}}\]
\[{\rm{S = }}\frac{{\rm{8}}}{{\rm{3}}}\]
Tính tổng S các nghiệm trên đoạn \[\left[ {{\rm{0; \pi }}} \right]\] của phương trình \[\left( {{\rm{1 + cosx}}} \right)\left( {{\rm{2sinx}} - {\rm{cosx}}} \right){\rm{ = si}}{{\rm{n}}^{\rm{2}}}{\rm{x}}\]
\[{\rm{S = }}\frac{{{\rm{2\pi }}}}{{\rm{3}}}\]
\[{\rm{S = \pi }}\]
\[{\rm{S = }}\frac{{\rm{\pi }}}{{\rm{2}}}\]
\[{\rm{S = 2\pi }}\]
Tìm số nghiệm trên đoạn \[\left[ {{\rm{0; }}\frac{{\rm{\pi }}}{{\rm{2}}}} \right]\]của phương trình\[{\rm{si}}{{\rm{n}}^{\rm{3}}}{\rm{x + sinxcosx = 1}} - {\rm{co}}{{\rm{s}}^{\rm{3}}}{\rm{x}}\]
3
4
2
1
Tìm m để phương trình\[\left( {{\rm{m}} - {\rm{1}}} \right){\rm{co}}{{\rm{s}}^{\rm{2}}}{\rm{x = m}}\]có nghiệm.
\[{\rm{m}} \le 0\]
\[0 \le {\rm{m}} \le 1\]
\[ - 1 \le {\rm{m}} \le 1\]
\( - 1 < m < 1\)
Tìm m để phương trình\[{\rm{tanx + cotx = 2m}}\] có nghiệm.
\[{\rm{m}} \ge 1\]
\[{\rm{m}} \in \mathbb{R}\bcancel{{}}\left( { - {\rm{1; 1}}} \right)\]
\[0 \le {\rm{m}} \le 1\]
m < 1
Nghiệm của phương trình \[{\mathop{\rm s}\nolimits} {\rm{in3x = cosx}}\]là
\[{\rm{x = k\pi ; x = k}}\frac{{\rm{\pi }}}{{\rm{2}}}\]
\[{\rm{x = }}\frac{{\rm{\pi }}}{{\rm{8}}}{\rm{ + k}}\frac{{\rm{\pi }}}{{\rm{2}}}{\rm{; x = }}\frac{{\rm{\pi }}}{{\rm{4}}}{\rm{ + k\pi }}\]
\[{\rm{x = k2\pi ; x = }}\frac{{\rm{\pi }}}{{\rm{2}}}{\rm{ + k2\pi }}\]
\[{\rm{x = k\pi ; x = }}\frac{{\rm{\pi }}}{{\rm{4}}}{\rm{ + k\pi }}\]
Tìm tập nghiệm của bất phương trình\[{\rm{ta}}{{\rm{n}}^{\rm{2}}}\left( {\frac{{\rm{\pi }}}{{\rm{2}}} - {\rm{x}}} \right){\rm{ = }}\frac{{{\rm{1 + sinx}}}}{{{\rm{sinx}}}}\]
\[\left\{ {\frac{{\rm{\pi }}}{{\rm{6}}}{\rm{ + }}\frac{{{\rm{k2\pi }}}}{{\rm{3}}}{\rm{;}} - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{ + k2\pi ,}}\,\,{\rm{k}} \in \mathbb{Z}} \right\}\]
\[\left\{ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{ + k2\pi ,}}\,\,{\rm{k}} \in \mathbb{Z}} \right\}\]
\[\left\{ {\frac{{\rm{\pi }}}{{\rm{6}}}{\rm{ + }}\frac{{{\rm{k2\pi }}}}{{\rm{3}}}{\rm{, }}\,{\rm{k}} \in \mathbb{Z}} \right\}\]
\[\left\{ {\frac{{\rm{\pi }}}{{\rm{6}}}{\rm{ + k\pi , }}\,{\rm{k}} \in \mathbb{Z}} \right\}\]
Nhiệt độ ngoài trời ờ một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \[{\rm{h(t) = 29 + 3sin}}\frac{{\rm{\pi }}}{{{\rm{12}}}}{\rm{(t}} - {\rm{9)}}\] với h tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ C và vào lúc mấy giờ?
(Theo https://www.sciencedirect.com/science/ article/abs/pii/0168192385900139)
32∘C, lúc 15 giờ.
29∘C, lúc 9 giờ.
26∘C, lúc 3 giờ.
26∘C, lúc 0 giờ.
Nghiệm âm lớn nhất của phương trình\[{\rm{cos}}\left( {{\rm{4x}} - \frac{{\rm{\pi }}}{{\rm{6}}}} \right){\rm{ + si}}{{\rm{n}}^{\rm{2}}}{\rm{x = co}}{{\rm{s}}^{\rm{2}}}{\rm{x}}\]
\[ - \frac{{35}}{{36}}{\rm{\pi }}\]
\[ - \frac{{11}}{{36}}{\rm{\pi }}\]
\[ - \frac{{{\rm{11\pi }}}}{{{\rm{12}}}}\]
\[ - \frac{{\rm{\pi }}}{{{\rm{12}}}}\]
Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình \[{\rm{x = 2cos}}\left( {{\rm{5t}} - \frac{{\rm{\pi }}}{{\rm{6}}}} \right){\rm{.}}\].Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
27.
26.
25.
28.
Tìm số nghiệm của phương trình sinx = cos2x thuộc đoạn\[\left[ {{\rm{0; 20\pi }}} \right]\].
20.
40.
30.
60.
Cho hàm số\[{\rm{f}}\left( {\rm{x}} \right){\rm{ = a}}{{\rm{x}}^{\rm{3}}}{\rm{ + b}}{{\rm{x}}^{\rm{2}}}{\rm{ + bx + c}}\]có đồ thị như hình vẽ:
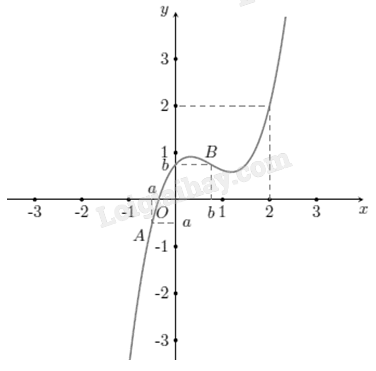
Số nghiệm nằm trong\[\left( {\frac{{ - {\rm{\pi }}}}{2};{\rm{3\pi }}} \right)\]của phương trình\[{\rm{f}}\left( {{\rm{cosx + 1}}} \right){\rm{ = cosx + 1}}\]là
2
3
5
4
