20 câu trắc nghiệm Toán 10 Chân trời sáng tạo Bài 4. Tích vô hướng của hai vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Cho \(\Delta ABC\) đều cạnh \(a\). Giá trị của tích vô hướng \(\overrightarrow {AB\,} \cdot \overrightarrow {AC\,} \) là
\(2a\).
\(\frac{1}{2}{a^2}\).
\({a^2}\).
\( - \frac{1}{2}{a^2}\).
Cho hình vuông \(ABCD\) có độ dài cạnh bằng \(2\). Tính \(\overrightarrow {AB} \cdot \overrightarrow {AD} \).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = 0\).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = 4\).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = \overrightarrow 0 \).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = - 4\).
Cho tam giác đều \(ABC\). Tính góc \(\left( {\overrightarrow {AB} ,\;\overrightarrow {BC} } \right)\).
\(120^\circ \).
\(60^\circ \).
\(30^\circ \).
\(150^\circ \).
Cho tam giác \(ABC\) có \(AB = 2\)cm, \(BC = 4\)cm, \(CA = 5\)cm. Tính \(\overrightarrow {CA} \cdot \overrightarrow {CB} \).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = 37\).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = \frac{{37}}{2}\).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = \frac{{37}}{{20}}\).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = - \frac{{37}}{2}\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 3\), \(\left| {\overrightarrow b } \right| = 2\) và \(\overrightarrow a \cdot \overrightarrow b = - 3\). Xác định số đo góc \(\alpha \)giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).
\(\alpha = 30 \circ \).
\(\alpha = 45 \circ \).
\(\alpha = 60 \circ \).
\(\alpha = 120 \circ \).
Một người dùng một lực \(\overrightarrow F \) có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. 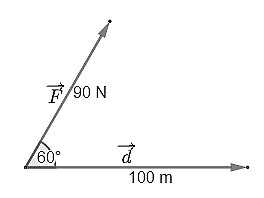
Biết lực \(\overrightarrow F \) hợp với hướng dịch chuyển một góc \(60^\circ \). Tính công sinh bởi lực \(\overrightarrow F \).
\(5400\,\,{\rm{(J)}}\).
\(4500\,\,{\rm{(J)}}\).
\(1500\,\,{\rm{(J)}}\).
\(450\,{\rm{(J)}}\).
Cho hình thang vuông \(ABCD\)có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\).Tính \(\overrightarrow {DA} \cdot \overrightarrow {BC} \).
\( - 9{a^2}\).
\(15{a^2}\).
\(0\).
\(9{a^2}\)
Cho tam giác \(ABC\) có \[BC = a,\,{\rm{ }}CA = b,{\rm{ }}AB = c\].Tính \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \cdot \overrightarrow {BC} \).
\(P = {b^2} - {c^2}\).
\(P = \frac{{{c^2} + {b^2}}}{2}\).
\(P = \frac{{{c^2} + {b^2} + {a^2}}}{3}\).
\(P = \frac{{{c^2} + {b^2} - {a^2}}}{2}\).
Cho hai vectơ \(\vec a,\vec b\) thỏa mãn: \(\left| {\vec a} \right| = 4;\left| {\vec b} \right| = 3;\left| {\vec a - \vec b} \right| = 4\). Gọi \(\alpha \) là góc giữa hai vectơ \(\vec a,\vec b\). Chọn phát biểu đúng.
\(\alpha = 60^\circ \).
\(\alpha = 30^\circ \).
\(\cos \alpha = \frac{1}{3}\).
\(\cos \alpha = \frac{3}{8}\).
Cho hình vuông \(ABCD\) cạnh bằng 3. Trên cạnh \(AB\) lấy điểm \[M\] sao cho \(BM = 1\), trên cạnh \[CD\] lấy điểm \[N\] sao cho \[DN = 1\] và \[P\] là trung điểm\[BC\]. Tính \[\cos \widehat {MNP}\].
\(\cos \widehat {MNP} = \frac{{13}}{{5\sqrt {10} }}\).
\(\cos \widehat {MNP} = \frac{{13}}{{4\sqrt {10} }}\).
\(\cos \widehat {MNP} = \frac{{13}}{{\sqrt {10} }}\).
\(\cos \widehat {MNP} = \frac{{13}}{{45\sqrt {10} }}\).
Phần II. Trắc nghiệm đúng, sai
Cho hình chữ nhật \(ABCD,AB = 4a,AD = 3a\). Gọi \(M\) là trung điểm của \(AB,G\) là trọng tâm tam giác \(ACM\).
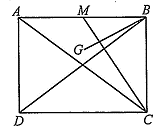
a) \(\overrightarrow {CM} = \frac{1}{2}\overrightarrow {BA} - 3\overrightarrow {BC} \).
b) \(\overrightarrow {BG} = \frac{3}{2}\overrightarrow {BA} + \frac{1}{3}\overrightarrow {BC} .\)
c) \(\overrightarrow {BC} \cdot \overrightarrow {BA} = 0\).
d) \(\overrightarrow {BG} \cdot \overrightarrow {CM} = - {a^2}.\)
Cho tam giác \(ABC\) có \(AB = 2a,AC = 3a,\,\widehat {BAC} = 60^\circ \). Gọi \(I\) là trung điểm đoạn thẳng \(BC\). Điểm \(J\) thuộc đoạn \(AC\) thỏa mãn \(12AJ = 7AC\).
a) \(\overrightarrow {AB} \cdot \overrightarrow {AC} = 4{a^2}\).
b) \(\overrightarrow {AI} = \frac{3}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} \).
c) \(\overrightarrow {BJ} = - \overrightarrow {AB} + \frac{7}{{12}}\overrightarrow {AC} \).
d) \(AI \bot BJ\).
Hai người cùng kéo một xe goòng. Người thứ nhất và người thứ hai lần lượt tác dụng vào chiếc xe goòng bằng hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hai lực vuông góc nhau, phương lực \(\overrightarrow {{F_2}} \) song song mặt đường) như hình vẽ và lực tổng hợp hợp với phương ngang (mặt đường) một góc \(30^\circ \). Người thứ nhất kéo một lực là \[40\sqrt 3 \] (N), người thứ hai kéo một lực là \[80\] (N).
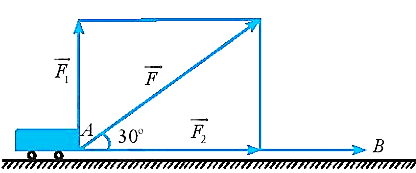
a) \(\left| {\overrightarrow {{F_1}} } \right| = 80,\left| {\overrightarrow {{F_2}} } \right| = 40\sqrt 3 \).
b) \(\left( {\overrightarrow {{F_2}} ,\overrightarrow F } \right) = 30^\circ \).
c) Độ lớn của \(\overrightarrow F \) bằng \(40\sqrt 7 \) (N).
d) Công sinh ra khi kéo vật đi một khoảng dài \(50\) (m) là \(a\sqrt b \) (J) thì tổng \(a + b = 1021\).
Cho hình vuông \(ABCD\) cạnh \(a\). Lấy \(E\) là trung điểm của \(BC\), điểm \(F\) thoả mãn \(\overrightarrow {BF} = \frac{3}{4}\overrightarrow {BD} \).
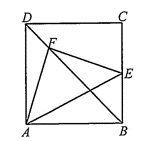
a) \(\overrightarrow {AE} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \).
b) \(\overrightarrow {AF} = \frac{1}{4}\overrightarrow {AB} + \frac{5}{4}\overrightarrow {AD} .\)
c) \(\overrightarrow {EF} = \frac{{ - 3}}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AD} .\)
d) Tam giác \(AEF\) vuông cân.
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = a,BC = 2a\).
a) \(\widehat {ACB} = 60^\circ \).
b) \(\overrightarrow {BA} \cdot \overrightarrow {BC} = {a^2}\).
c) \(\overrightarrow {BC} \cdot \overrightarrow {CA} = 3{a^2}.\)
d) \(\overrightarrow {AB} \cdot \overrightarrow {BC} + \overrightarrow {BC} \cdot \overrightarrow {CA} + \overrightarrow {CA} \cdot \overrightarrow {AB} = - 4{a^2}\).
Phần III. Trắc nghiệm trả lời ngắn
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \). Biết \(\left| {\overrightarrow a } \right| = 3,\left| {\overrightarrow b } \right| = 2\) và \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 120^\circ \). Tính \(\left| {\overrightarrow a - 2\overrightarrow b } \right|\) (kết quả làm tròn đến hàng phần chục).
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = 30^\circ ,AC = 2\). Gọi \(M\) là trung điểm của \(BC.\) Tính giá trị của biểu thức \(P = \overrightarrow {AM} \cdot \overrightarrow {BM} .\)
Một vật nằm trên mặt phẳng ngang chịu tác dụng của hai lực \[\overrightarrow {{F_1}} \] có phương song song với mặt phẳng ngang và \[\overrightarrow {{F_2}} \] theo phương tạo với mặt phẳng ngang một góc \[60^\circ \](như hình vẽ). Biết rằng độ lớn của các lực là \[\left| {\overrightarrow {{F_1}} } \right| = 50\,{\rm{N}}\], \[\left| {\overrightarrow {{F_2}} } \right| = 30\,{\rm{N}}\]. Ta nhận thấy vật di chuyển theo phương nằm ngang một quãng đường \[28\]m.
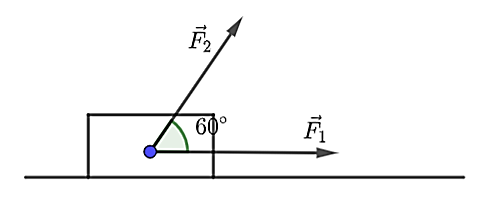
Tính công sinh ra (đơn vị: Jun) bởi lực \(\overrightarrow F \) là hợp lực của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) nói trên.
Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ \(700\) (km/h) thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ \(40\) (km/h). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm vận tốc mới của máy bay (kết quả làm tròn đến hàng đơn vị theo đơn vị km/h).
Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực (đơn vị KJ và làm tròn đến hàng đơn vị) tác động lên xe, biết dốc dài 50 m và nghiêng \(15^\circ \) so với phương nằm ngang (trong tính toán, lấy gia tốc trọng trường bằng \(10\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}\)).



