10 câu hỏi
Phần I: Trắc nghiệm nhiều phương án lựa chọn
Tập xác định của hàm số \[y = \frac{{x - 3}}{{2x - 2}}\] là
\(\mathbb{R}\backslash \left\{ 1 \right\}\).
\(\mathbb{R}\backslash \left\{ 3 \right\}\).
\(\mathbb{R}\backslash \left\{ 2 \right\}\).
\(\left( {1; + \infty } \right)\).
Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?
\(y = \frac{{2\sqrt x }}{{{x^2} + 4}}\).
\(y = {x^2} - \sqrt {{x^2} + 1} - 3\).
\(y = \frac{{3x}}{{{x^2} - 4}}\).
\(y = {x^2} - 2\sqrt {x - 1} - 3\).
Với giá trị nào của \(m\) thì hàm số \(y = \frac{{2x + 1}}{{{x^2} - 2x - 3 - m}}\) xác định trên \(\mathbb{R}\).
\(m \le - 4\).
\(m < - 4\).
\(m > 0\).
\(m < 4\).
Xét sự biến thiên của hàm số \(f\left( x \right) = \frac{3}{x}\) trên khoảng \(\left( {0; + \infty } \right)\). Khẳng định nào sau đây đúng?
Hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số vừa đồng biến, vừa nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số không đồng biến, không nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Cho hàm số \(y = {x^3} - 3x + 2\). Điểm nào sau đây thuộc đồ thị hàm số đã cho?
\(\left( { - 2;0} \right)\).
\(\left( {1;1} \right)\).
\(\left( { - 2; - 12} \right)\).
\(\left( {1; - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( { - \infty ; + \infty } \right)\) có đồ thị như hình vẽ dưới đây.
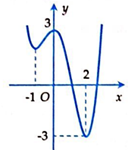
Mệnh đề nào sau đây đúng?
Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 3;0} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
Cho hàm số . Giá trị lớn nhất của hàm số trên \(\left[ { - 2;2} \right]\) là:
2
4.
5.
7.
Tìm giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^2} + {\left( {x - 3} \right)^2}\).
0.
\(\frac{9}{2}\).
\(\frac{{ - 9}}{2}\).
\(\frac{3}{2}\).
Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng \(x + y\) để diện tích hình thang\[EFGH\] đạt giá trị nhỏ nhất.
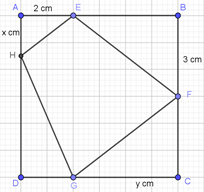
\[x + y = \frac{{7\sqrt 2 }}{2}\].
\[x + y = \frac{{3\sqrt 2 }}{2}\].
\[x + y = \frac{{\sqrt 2 }}{2}\].
\[x + y = \frac{{5\sqrt 2 }}{2}\].
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) thỏa mãn \(f\left( {x + \frac{1}{x}} \right) = {x^3} + \frac{1}{{{x^3}}}\forall x \ne 0\). Tính \(f\left( 3 \right)\).
\(f\left( 3 \right) = 36\).
\(f\left( 3 \right) = 18\).
\(f\left( 3 \right) = 29\).
\(f\left( 3 \right) = 25\).
