10 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Cho \(\Delta ABC\) đều cạnh \(a\). Giá trị của tích vô hướng \(\overrightarrow {AB\,} \cdot \overrightarrow {AC\,} \) là
\(2a\).
\(\frac{1}{2}{a^2}\).
\({a^2}\).
Cho hình vuông \(ABCD\) có độ dài cạnh bằng \(2\). Tính \(\overrightarrow {AB} \cdot \overrightarrow {AD} \).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = 0\).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = 4\).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = \overrightarrow 0 \).
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = - 4\).
Cho tam giác đều \(ABC\). Tính góc \(\left( {\overrightarrow {AB} ,\;\overrightarrow {BC} } \right)\).
\(120^\circ \).
\(60^\circ \).
\(30^\circ \).
\(150^\circ \).
Cho tam giác \(ABC\) có \(AB = 2\)cm, \(BC = 4\)cm, \(CA = 5\)cm. Tính \(\overrightarrow {CA} \cdot \overrightarrow {CB} \).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = 37\).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = \frac{{37}}{2}\).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = \frac{{37}}{{20}}\).
\(\overrightarrow {CA} \cdot \overrightarrow {CB} = - \frac{{37}}{2}\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 3\), \(\left| {\overrightarrow b } \right| = 2\) và \(\overrightarrow a \cdot \overrightarrow b = - 3\). Xác định số đo góc \(\alpha \)giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).
\(\alpha = 30 \circ \).
\(\alpha = 45 \circ \).
\(\alpha = 60 \circ \).
\(\alpha = 120 \circ \).
Một người dùng một lực \(\overrightarrow F \) có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m.
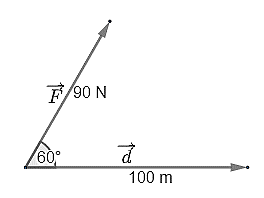
Biết lực \(\overrightarrow F \) hợp với hướng dịch chuyển một góc \(60^\circ \). Tính công sinh bởi lực \(\overrightarrow F \).
\(5400\,\,{\rm{(J)}}\).
\(4500\,\,{\rm{(J)}}\).
\(1500\,\,{\rm{(J)}}\).
\(450\,{\rm{(J)}}\).
Cho hình thang vuông \(ABCD\)có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\).Tính \(\overrightarrow {DA} \cdot \overrightarrow {BC} \).
\( - 9{a^2}\).
\(15{a^2}\).
\(0\).
\(9{a^2}\)
Cho tam giác \(ABC\) có \[BC = a,\,{\rm{ }}CA = b,{\rm{ }}AB = c\].Tính \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \cdot \overrightarrow {BC} \).
\(P = {b^2} - {c^2}\).
\(P = \frac{{{c^2} + {b^2}}}{2}\).
\(P = \frac{{{c^2} + {b^2} + {a^2}}}{3}\).
\(P = \frac{{{c^2} + {b^2} - {a^2}}}{2}\).
Cho hai vectơ \(\vec a,\vec b\) thỏa mãn: \(\left| {\vec a} \right| = 4;\left| {\vec b} \right| = 3;\left| {\vec a - \vec b} \right| = 4\). Gọi \(\alpha \) là góc giữa hai vectơ \(\vec a,\vec b\). Chọn phát biểu đúng.
\(\alpha = 60^\circ \).
\(\alpha = 30^\circ \).
\(\cos \alpha = \frac{1}{3}\).
\(\cos \alpha = \frac{3}{8}\).
Cho hình vuông \(ABCD\) cạnh bằng 3. Trên cạnh \(AB\) lấy điểm \[M\] sao cho \(BM = 1\), trên cạnh \[CD\] lấy điểm \[N\] sao cho \[DN = 1\] và \[P\] là trung điểm\[BC\]. Tính \[\cos \widehat {MNP}\].
\(\cos \widehat {MNP} = \frac{{13}}{{5\sqrt {10} }}\).
\(\cos \widehat {MNP} = \frac{{13}}{{4\sqrt {10} }}\).
\(\cos \widehat {MNP} = \frac{{13}}{{\sqrt {10} }}\).
\(\cos \widehat {MNP} = \frac{{13}}{{45\sqrt {10} }}\).
