10 câu hỏi
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình\[\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 0}\end{array}} \right.\]?
\[\left( { - 1;4} \right)\].
\[\left( { - 2;4} \right)\].
\[\left( {0;0} \right)\].
\[\left( { - 3;4} \right)\].
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \[\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x +y + 1 < 0}\end{array}} \right.\]?
\[\left( {0;0} \right)\].
\[\left( {1;0} \right)\].
\[\left( {0; - 2} \right)\].
\[\left( {0;2} \right)\].
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.\) có tập nghiệm là \(S\). Khẳng định nào sau đây là khẳng định đúng?
\(\left( {1;1} \right) \in S\).
\(\left( { - 1; - 1} \right) \in S\).
\(\left( {1; - \frac{1}{2}} \right) \in S\).
\(\left( { - \frac{1}{2};\frac{2}{5}} \right) \in S\).
Miền tam giác \[ABC\] kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?
![Miền tam giác \[ABC\] kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid0-1753191540.png)
\[\left\{ \begin{array}{l}y \ge 0\\5x - 4y \ge 10\\5x + 4y \le 10\end{array} \right.\].
\(\left\{ \begin{array}{l}x > 0\\5x - 4y \le 10\\4x + 5y \le 10\end{array} \right.\).
\(\left\{ \begin{array}{l}x \ge 0\\4x - 5y \le 10\\5x + 4y \le 10\end{array} \right.\).
\(\left\{ \begin{array}{l}x \ge 0\\5x - 4y \le 10\\4x + 5y \le 10\end{array} \right.\).
Cho hệ \(\left\{ \begin{array}{l}2x + 3y < 5\,\,\,(1)\\x + \frac{3}{2}y < 5\,\,\,(2)\end{array} \right.\). Gọi \({S_1}\) là tập nghiệm của bất
phương trình (1), \({S_2}\) là tập nghiệm của bất phương trình (2) và \(S\) là tập nghiệm của hệ thì
\({S_1} \subset {S_2}\).
\({S_2} \subset {S_1}\).
\({S_2} = S\).
\({S_1} \ne S\).
Phần không tô màu là hình biểu diễn miền nghiệm của hệ bất phương trình nào?
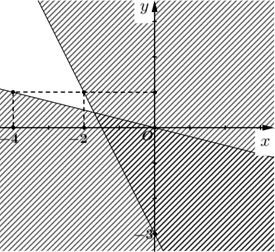
\(\left\{ \begin{array}{l}x + 4y > 0\\2x + y + 3 > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 4y < 0\\2x + y + 3 \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 4y > 0\\2x + y + 3 \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 4y \ge 0\\2x + y + 3 \ge 0\end{array} \right.\).
Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định bởi hệ là
\(\min F = 1\) khi \(x = 2\), \(y = 3\).
\(\min F = 2\) khi \(x = 0\), \(y = 2\).
\(\min F = 3\) khi \(x = 1\), \(y = 4\).
\(\min F = 0\) khi \(x = 0\), \(y = 0\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\3x + 5y \le 15\\x \ge 0\\y \ge 0\end{array} \right.\). Khẳng định nào sau đây là
khẳng định sai?
Trên mặt phẳng tọa độ \(Oxy\), biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác \(ABCO\) kể cả các cạnh với \(A\left( {0;3} \right)\), \(B\left( {\frac{{25}}{8};\frac{9}{8}} \right)\), \(C\left( {2;0} \right)\) và \(O\left( {0;0} \right)\).
Đường thẳng \(\Delta :x + y = m\) có giao điểm với tứ giác \(ABCO\) kể cả khi \( - 1 \le m \le \frac{{17}}{4}\).
Giá trị lớn nhất của biểu thức \(x + y\), với \(x\) và \(y\) thỏa mãn hệ bất phương trình đã cho là \(\frac{{17}}{4}\).
Giá trị nhỏ nhất của biểu thức \(x + y\), với \(x\) và \(y\) thỏa mãn hệ bất phương trình đã cho là 0.
Giá trị lớn nhất của biết thức \[F\left( {x;y} \right) = x + 2y\] với điều kiện là
\[6\].
\[8\].
\[10\].
\[12\].
Biểu thức \[F = y--x\] đạt giá trị nhỏ nhất với điều kiện có toạ độ là
\[\left( {4;1} \right)\].
\[\left( {3;1} \right)\].
\[\left( {2;1} \right)\].
\[\left( {1;1} \right)\].
