15 câu hỏi
Điền nội dung phù hợp vào chỗ trống: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng … với đường thẳng kia.”
vuông góc;
song song;
trùng nhau;
cắt nhau.
Ta có a, b phân biệt; nếu a // c và b // c thì:
\[a \bot b\];
\[a \equiv b\];
\[a \cap b\];
a // b.
Điền cụm từ thích hợp vào chỗ trống: “Nếu một đường thẳng cắt hai đường thẳng … thì hai góc đồng vị bằng nhau.”
song song;
vuông góc;
giao nhau;
trùng nhau.
Cho hình vẽ bên dưới. Tính \[\widehat {{I_1}}\], biết \[\widehat {{J_3}} = 26^\circ \]và x // y.
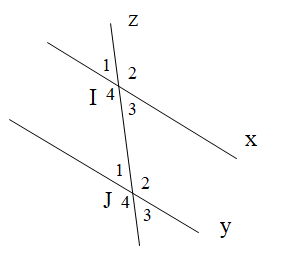
96o
125o
55o
26o
Cho hình vẽ như bên dưới. Tính \[\widehat {{M_3}}\], biết \[\widehat {{N_2}} = 137^\circ \].
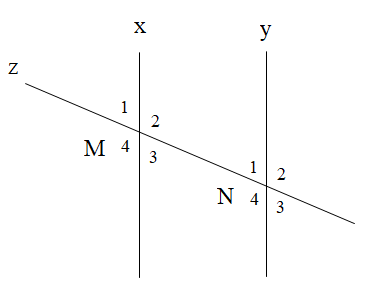
137o
43o;
37o;
149o.
Nếu đường thẳng t cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì:
Hai đường thẳng x, y trùng nhau;
Hai đường thẳng x, y cắt nhau;
Hai đường thẳng x, y song song với nhau;
Hai đường thẳng x, y vuông góc với nhau.
Qua điểm M nằm ngoài đường thẳng a, ta vẽ ba đường thẳng qua M và song song với a thì:
Ba đường thẳng song song;
Ba đường thẳng cắt nhau tại A;
Ba đường thẳng vuông góc;
Ba đường thẳng đó trùng nhau.
Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.
0;
1;
2;
vô số.
Cho hình vẽ. Nếu a // b thì:
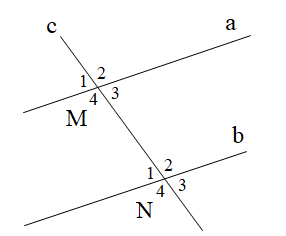
\[\widehat {{M_1}} = \widehat {{N_2}}\];
\[\widehat {{M_3}} = \widehat {{N_4}}\];
\[\widehat {{M_4}} = \widehat {{N_4}}\];
\[\widehat {{M_4}} = \widehat {{N_3}}\].
Cho hình vẽ như bên dưới. Tính \[\widehat {{N_3}}\], biết a // b và \[\widehat {{M_1}} = 50^\circ \].
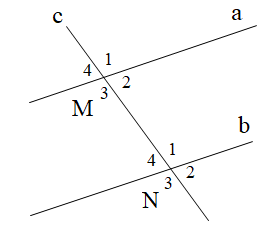
50o;
60o;
65o;
85o.
Cho hai điểm phân biệt H, K. Ta vẽ một đường thẳng x đi qua điểm H và một đường thẳng y đi qua điểm K sao cho x // y. Có thể vẽ được bao nhiêu cặp đường thẳng x, y thỏa mãn điều kiện trên.
Ba cặp;
Bốn cặp;
Một cặp;
Vô số cặp.
Cho hình vẽ bên dưới. Tính số đo góc OHC, biết MN // BC và \[\widehat {AOM} = 59^\circ \]
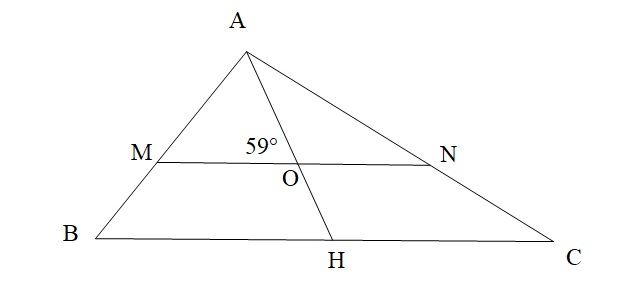
69°;
121°;
59°;
130°.
Cho hình bình hành ABCD như hình vẽ. Tính số đo góc AIJ.
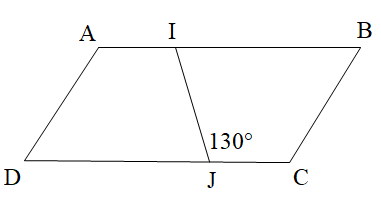
65°;
100°;
70°;
130°.
Cho hình thang ABCD như hình vẽ. Tính góc BAC, biết AC là tia phân giác góc BCD.
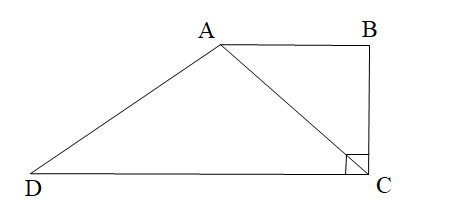
90°;
45°;
120°;
65°.
Cho hình vẽ bên dưới. Tính góc \[{M_2}\], biết a // b và \[{N_1} = 40^\circ \].
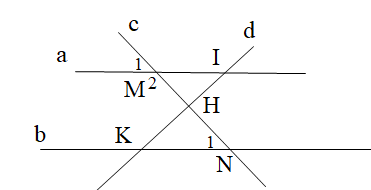
140o;
120o;
40o;
60o.
