15 câu hỏi
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 2x + 1 là:




Biểu thức nào sau đây là tam thức bậc hai
f(x) = x + 2;
f(x) = 2x3 + 2x2 – 1;
f(x) = x2 – 3x;
f(x) = 2x – 1.
Với x thuộc tập hợp nào dưới đây thì đa thức f(x) = x2 – 6x + 8 không dương?
[2; 3];
;
[2; 4];
[1; 4].
Các giá trị m làm cho biểu thức f(x) = x2 + 4x + m + 3 luôn dương là
m < 1;
m ≥ 1;
m > 1;
\[m \in \emptyset \].
Tam thức nào sau đây nhận giá trị âm với mọi x < 1
f(x) = x2 – 5x +6 ;
f(x) = x2 – 16;
f(x) = x2 + 2x + 3;
f(x) = – x2 + 5x – 4.
Cho hàm số f(x) = mx2 – 2mx + m – 1. Giá trị của m để f(x) < 0 \(\forall x \in \mathbb{R}\).
m ≥ 0;
m > 0;
m < 0;
m ≤ 0.
Tìmtất cả các giá trị thực của tham số m để f(x) = (m – 3)x2 + (m + 2)x – 4 nhận giá trị không dương với mọi giá trị của x.
\[\left[ \begin{array}{l}m \le - 22\\m \ge 2\end{array} \right.\];
– 22 ≤ m ≤ 2;
– 22 < m < 2;
\[\left[ \begin{array}{l} - 22 \le m \le 2\\m = 3\end{array} \right.\].
Tìm tất cả các giá trị của m để tam thức f(x) = mx2 – x + m luôn dương với \(\forall x \in \mathbb{R}\)
m > 0;
m < 0;
\(m > \frac{1}{2}\);
\(m < \frac{1}{2}\).
Tam thức y = – x2 – 3x – 4 nhận giá trị âm khi và chỉ khi
x < 4 hoặc x > – 1;
x < 1 hoặc x > 4;
– 4 < x < 4;
x \( \in \) ℝ.
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x \( \in \) ℝ.
m < – 1;
m < 0;
– 1 < m < 0;
m < 1 và m ≠ 0.
Xác định m để biểu thức f(x) = (m + 2)x2 – 3mx + 1 là tam thức bậc hai
m = 2;
m = – 2;
m ≠ 2;
m ≠ – 2.
Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi
m ≤ - 4 hoặc m ≥ 0;
m < - 4 hoặc m > 0;
– 4 < m < 0;
m < 0 hoặc m > 4.
Các giá trị m để tam thức f(x) = x2 – (m + 2)x + 8m + 1 đổi dấu 2 lần là
m ≤ 0 hoặc m ≥ 28;
m < 0 hoặc m > 28;
0 < m < 28;
m > 0.
Cho tam thức f(x) = x2 + 2mx + 3m – 2. Tìm m để f(x) ≥ 0 với mọi x \( \in \) ℝ.
1 ≤ m ≤ 2;
1 < m < 2;
m < 1;
m > 2.
Cho tam thức bậc hai f(x) = ax2 + bx + c có đồ thị như hình vẽ dưới đây
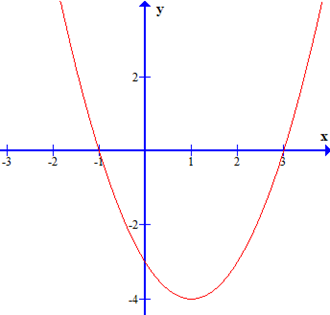
Bảng biến thiên của tam thức bậc hai là




