25 câu hỏi
Tìm số phức z thỏa mãn hệ thức và
z = 3 + 4i; z = 5.
z = 3 + 4i; z = -4.
z = -3 + 4i; z = 5.
z = 3 - 4i; z = -5.
Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
x = -2; y = 2.
x = 2; y = ±2.
x = 2; y = 2.
x = -2; y = ±2.
Cho số phức z thỏa mãn z2 - 6z + 13 = 0 . Giá trị của là:
Cho số phức z thỏa . Viết z dưới dạng z = a + bi. Khi đó tổng a + b có giá trị bằng bao nhiêu?
3.
-1.
1.
2.
Có bao nhiêu số phức z thỏa mãn: và
2.
3.
0.
1.
Tìm số phức z để
z = 0; z = 1 - i.
z = 0; z = 1 + i.
z = 0; z = 1 + i; z = 1 - i.
z = 1+ i; z = 1- i.
Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn z3 = 18 + 26i
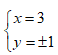
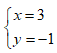
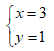
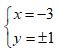
Cho số phức z = 3+ i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
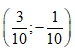
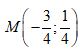
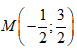
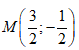
Căn bậc hai của số phức z = -3 + 4i có kết quả:
1 + 2i.
1 - 2i.
1 + 3i.
Tất cả sai.
Tính căn bậc hai của số phức z = 8 + 6i ra kết quả:
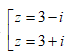
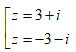
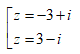
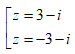
Cho z = 3 + 4i. Tìm căn bậc hai của z.
-2 + i và 2 - i
2 + ivà 2 - i
2 + i và -2 - i
3 - 2i và 2 - 3i
Gọi z là căn bậc hai có phần ảo âm của 33 - 56i. Phần thực của z là:
6.
7.
4.
–4.
Trong C , căn bậc hai của -121 là:
-11i.
11i.
-11.
11i và -11i.
Trong C, phương trình z2 + 3iz + 4 = 0 có nghiệm là:
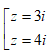
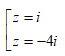
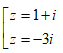
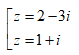
Cho z = 1 - i. Tìm căn bậc hai dạng lượng giác của z:
Trong C, phương trình (z2 + i) (z2 – 2iz – 1) = 0 có nghiệm là:
![]()
1 - i; -1+ i; 2i
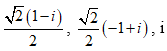
1 - 2i; -15i; 3i
Trong C, phương trình có nghiệm là:
![]()
![]()
![]()
![]()
Trong C, phương trình 2x2 + x + 1 = 0 có nghiệm là:
![]()
![]()
![]()
![]()
Trong C, phương trình z2 - z + 1 = 0 có nghiệm là:
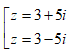
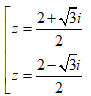
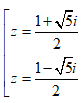
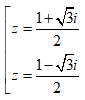
Gọi z1; z2 là hai nghiệm phức của phương trình z2 - 4z + 9 = 0; gọi M và N lần lượt là các điểm biểu diễn z1; z2 trên mặt phẳng phức. Tính độ dài đoạn thẳng MN.
1
2
Tìm các số thực b,c để phương trình z2 + bz + c = 0 nhận z = 1+ i làm một nghiệm.
b = -2; c = 3
b = -1; c = 2
b = -2; c = 2
b = 2; c = 2
Viết số phức sau dưới dạng lượng giác:
![]()
![]()
![]()
![]()
Viết số phức sau dưới dạng lượng giác:
![]()
![]()
![]()
![]()
Viết số phức sau dưới dạng lượng giác: (1 + 3i)( 1 + 2i)
![]()
![]()
![]()
![]()
Viết số phức sau dưới dạng lượng giác:
![]()
![]()
![]()
![]()








