30 CÂU HỎI
Cho số phức z = ( 3 - 2i)(1 + i) 2 . Môđun của là
A.2.
B.
C. 1.
D.
Cho số phức z thỏa mãn điều kiện . Môđun của số phức W = 1 + 2z + z2 có giá trị là:
A. 10.
B. -10.
C. 100.
D. -100.
Cho số phức z = -3 + 2i. Tính P = |z + 1 – i|.
A. P = 4.
B. P = 1.
C.
D.
Cho hai số phức z1 = 3 - 2i; z2 = -2 + i Tính P = | z1 + z2|.
A. P = 2.
B.
C. P = 1/2.
D. P = 2.
Cho hai số phức z1 = 3 + i; z2 = 2 - i. Tính P = | z1 + z1 z2|.
A. P = 10.
B. P = 50.
C. P = 5.
D. P = 85.
Cho số phức z thỏa mãn điều kiện: . Phần ảo của số phức w = 1 - iz + z là
A. 1.
B. -3.
C. -2.
D. -1.
Tìm phần thực, phần ảo của số phức z thỏa ( – i)(1 - i) = ( 1 + i) 3979
A. Phần thực là 21990 và phần ảo là 2.
B. Phần thực là - 21990 và phần ảo là 2.
C. Phần thực là -21989 và phần ảo là 1.
D. Phần thực là 21989 và phần ảo là 1.
Cho số phức z thỏa z = 1+ i+ i2+ i3+...+ i2016. Khi đó phần thực và phần ảo của z lần lượt là
A. 0 và -1.
B. 0 và 1.
C. 1 và 1.
D. 1 và 0.
Giá trị của biểu thức S = 1+ i2+ i4+ ...+ i4k là
A. 1.
B. 0.
C. 2.
D. ik.
Cho số phức z = 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là
A.
B.
C.
D.
Cho số phức z = x + y.i thỏa mãn z3 = 2 - 2i. Cặp số là(x;y)
A. (2; 2).
B. (-1; -1).
C. (3;-3).
D. (2; -3).
Cho số phức z = 3 + i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A.
B. 
C. 
D. 
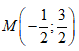
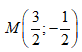
Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức w = 2 + 3i. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai điểm A và B đối xứng nhau qua trục tung.
B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
C. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.
D. Hai điểm A và B đối xứng nhau qua trục hoành.
Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A.
B.
C.
D.
Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – (1+ i)| = |z + 2i| là đường nào sau đây?
A. Đường thẳng.
B. Đường tròn.
C. Elip.
D. Parabol.
Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện
A. Tập hợp những điểm Mlà đường thẳng có phương trình 4x + 2y + 3 = 0.
B. Tập hợp những điểm M là đường thẳng có phương trình 4x - 2y + 3 = 0.
C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y - 3 = 0.
D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y + 3 = 0.
Tập hợp các điểm M biểu diễn số phức z thoả mãn |z – 2 + 5i| = 4 là:
A. Đường tròn tâm I(2 ; -5) và bán kính bằng 2.
B. Đường tròn tâm I(-2 ; 5) và bán kính bằng 4.
C. Đường tròn tâm I(2 ; -5) và bán kính bằng 4.
D. Đường tròn tâm O và bán kính bằng 2.
Cho z là số phức thỏa mãn là số thuần ảo. Tìm khẳng định đúng
A.
B. |z| = 1
C. |z| = 2
D.
Cho số phức z thỏa mãn là số thực. Khẳng định nào sau đây sai
A. z là số thực.
B. z là số ảo.
C. |z| = z.
D.
Cho các số thực a; b; c và d thỏa mãn: a+ bi= ( c+ di) n. Tìm khẳng định đúng
A. a2 + b2 = 2( c2 + d2) n
B. a2 + b2 = c2 + d2
C. a2 + b2 = 2n( c2 + d2)
D. a2 + b2 = ( c2 + d2)n
Tính tổng modul của các số phức z thỏa mãn z2 + |z| = 0
A. 1.
B. 2.
C. 3.
D. 4.
Có bao nhiêu số phức z thỏa mãn:
A. 1.
B. 2.
C. 3.
D. 4.
Có bao nhiêu số phức z thỏa mãn: z2 + |z| = .
A. 1.
B. 2.
C. 3.
D. 4.
Tìm các số phức z thỏa mãn:
A. z = 0
B.
C.
D. Tất cả đúng.
Tìm phần thực của số phức z thỏa mãn
A. 0.
B. 1.
C. 3.
D. 4.
Giải phương trình sau đây (2 + i)z = z + 2i - 1
A. z = 1 + i.
B. z = + i.
C. z = 2+ i.
D. Đáp án khác.
Tìm tổng phần thực và phần ảo của số phức z thỏa mãn: (1 - i) ( z - 2i) = 2 + i.
A. 4.
B. 3.
C. 5.
D. 7.
Giải phương trình sau đây :
A. z = 2.
B. z = -1.
C. z = -i.
D. z = 2i.
Tính tổng phần thực và phần ảo cùa số phức z thỏa mãn điều kiện sau:
A. 15.
B. 20.
C. 23.
D. 27.
Phần thực của số z thỏa mãn phương trình: (5 - 4i) z = ( 3 + 2i)(4 - i) gần với giá trị nào nhất.
A. 1,21.
B. 1,22.
C. 1,23.
D. 1,24.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
