10 câu hỏi
Đồ thị hàm số nào dưới đây có dạng như đường cong dưới đây?
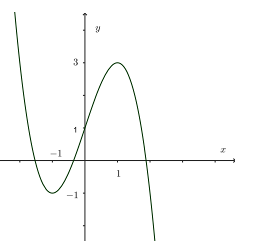
\[y = \frac{{2x - 1}}{{x + 1}}\];
\[y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\];
y = −x3 + 3x + 1;
y = x3 – 3x + 1.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
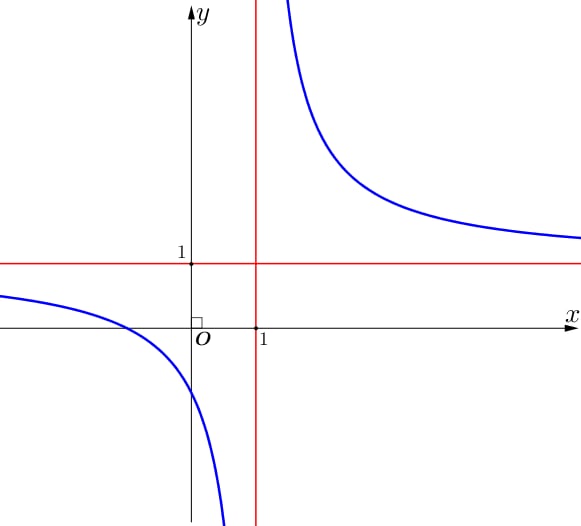
\(y = \frac{{x + 2}}{{x + 1}}\);
\(y = \frac{{x - 1}}{{x + 1}}\);
\(y = \frac{{ - 2x + 1}}{{x - 1}}\);
\(y = \frac{{x + 1}}{{x - 1}}\).
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
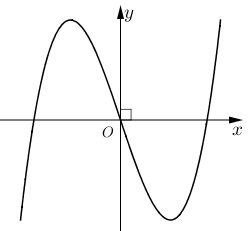
y = x3 – 3x;
y = −x3 + 3x;
y = x3 – 3x2 + 1;
y = −x3 + 3x2.
Hàm số nào dưới đây có bảng biến thiên như sau?
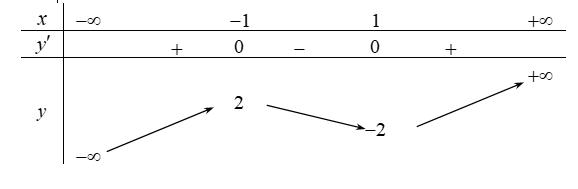
y = −x3 + 3x;
y = x3 – 3x;
y = −x2 + 2x;
y = x2 – 2x.
Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị như hình vẽ dưới đây. Chọn khẳng định đúng về dấu của a, b, c, d?
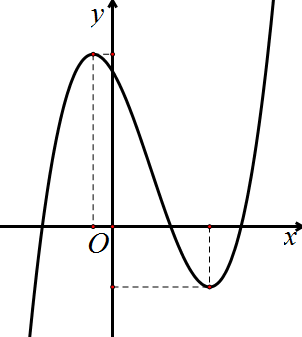
a > 0, b > 0, c > 0, d > 0;
a > 0, c > 0 > b, d < 0;
a > 0, b > 0, c > 0, d > 0;
a > 0, b < 0, c < 0, d > 0.
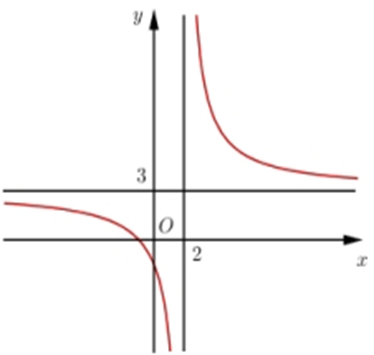
Đường cong trong hình là đồ thị của hàm số nào dưới đây?
\(y = \frac{{{x^2} - 2x - 3}}{{x - 2}}\);
\(y = \frac{{{x^2} - 2x}}{{x - 1}}\);
\(y = \frac{{{x^2} - 3x}}{{x - 2}}\);
\(y = \frac{{{x^2} + 3x}}{{x + 1}}\).
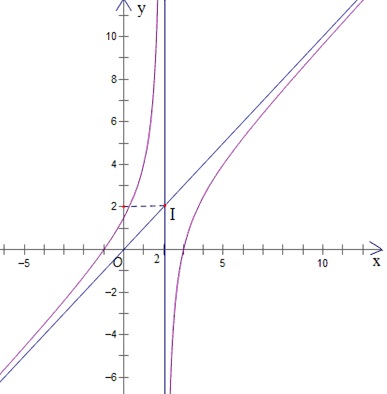
Đường cong ở hình bên dưới là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với a, b, c, d là các số thực.
Mệnh đề nào dưới đây đúng?
y' > 0, ∀x ≠ 2;
y' > 0, ∀x ≠ 3;
y' < 0, ∀x ≠ 2;
y' < 0, ∀x ≠ 3.
Đường cong ở hình dưới đây là đồ thị của hàm số
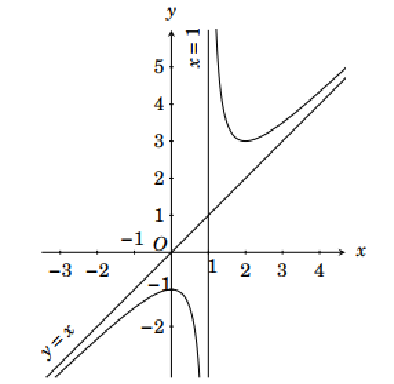
\(y = \frac{{{x^2} + x - 1}}{{x - 1}}\);
\(y = \frac{{{x^2} - x + 1}}{{x - 1}}\);
\(y = \frac{{{x^2} - 4x - 1}}{{x + 1}}\);
\[y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\].
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
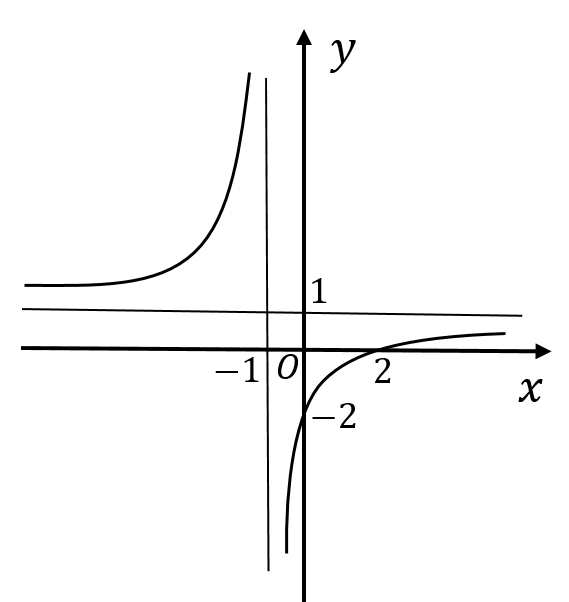
(0; −2);
(2; 0);
(−2; 0);
(0; 2).
Cho hàm số y = f(x) có đồ thị như hình bên. Số giao điểm của đồ thị với đường thẳng \(y = \frac{5}{2}\) là?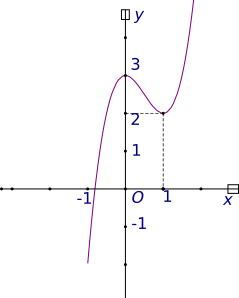
2;
1;
3;
0.
