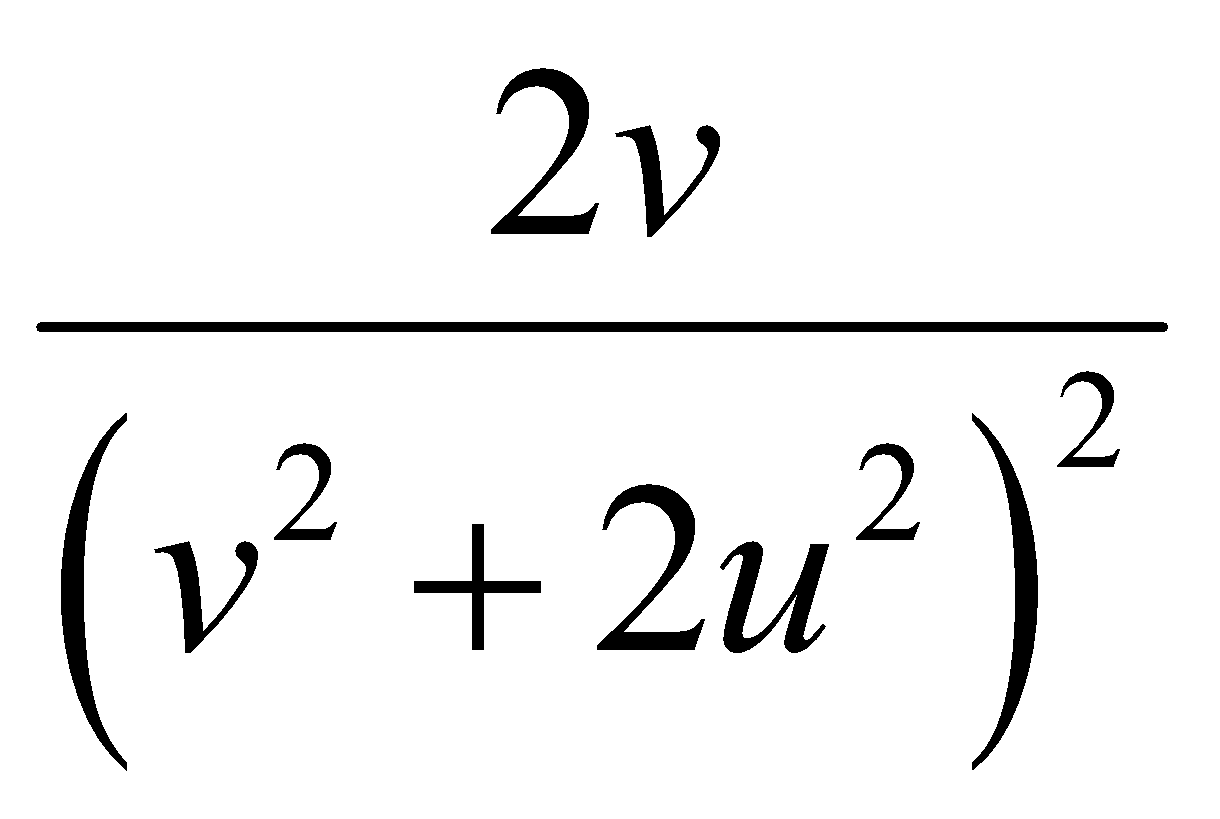25 CÂU HỎI
Cho f'(x) = x(2x+1)². Đồ thị hàm số f(x) có hoành độ các điểm uốn là
A. x=0
B. x = 0 và x = ![]()
C. x =![]() và x =
và x = ![]()
D. x =![]()
Người ta ước tính rằng chi phí để xây dựng 1 tòa nhà văn phòng cao n tầng là C(n) = 2n²+700n+1000 nghìn đôla. Hỏi nên xây tòa nhà đó bao nhiêu tầng để tối thiểu hóa chi phí xây dựng trung bình cho 1 tầng? (Đáp án lấy giá trị nguyên)
A. 25 tầng
B. 19 tầng
C. 22 tầng
D. 23 tầng
Cho hàm số f(x;y) = ![]() . Đạo hàm riêng của hàm số theo biến y tại điểm (0;1) là
. Đạo hàm riêng của hàm số theo biến y tại điểm (0;1) là
A. 1
B. 2
C. 3
D. 4
Cho hàm số có đạo hàm f'(x) = 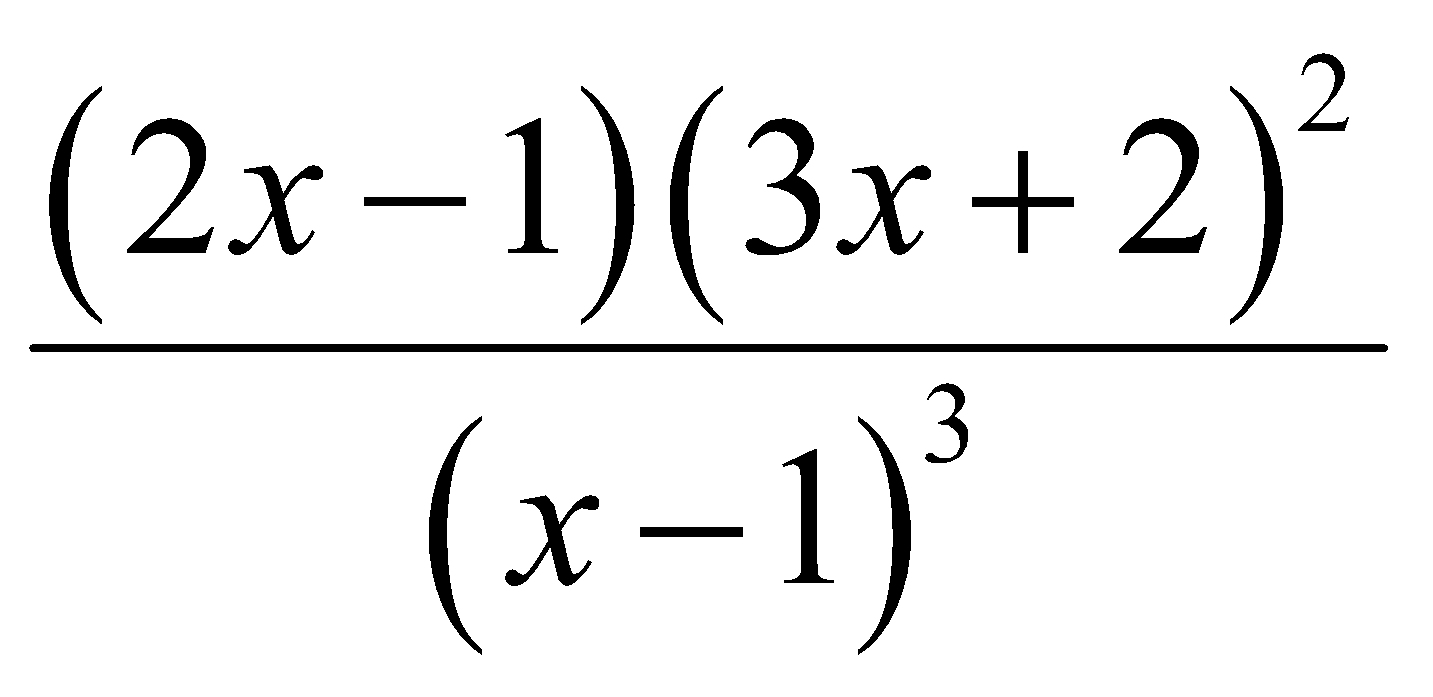 Hàm số f(x) giảm trong khoảng nào dưới đây:
Hàm số f(x) giảm trong khoảng nào dưới đây:
A. 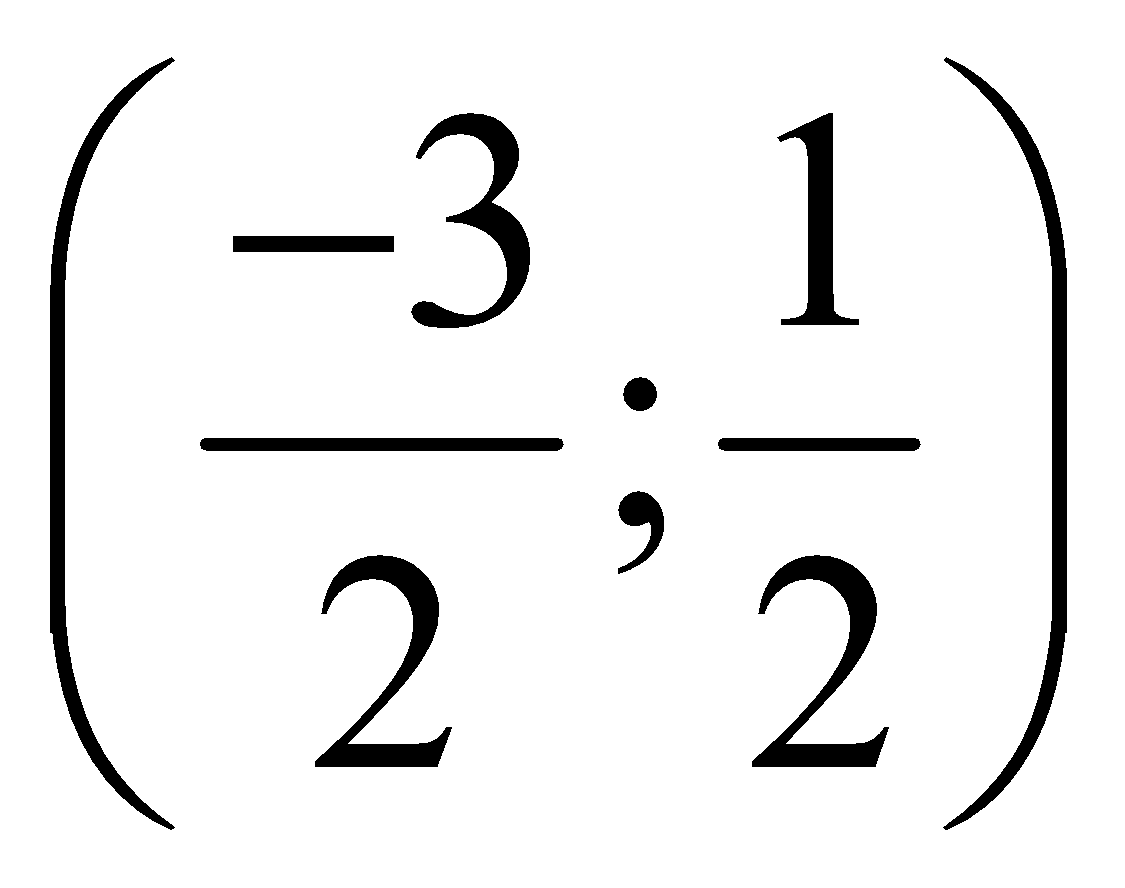
B.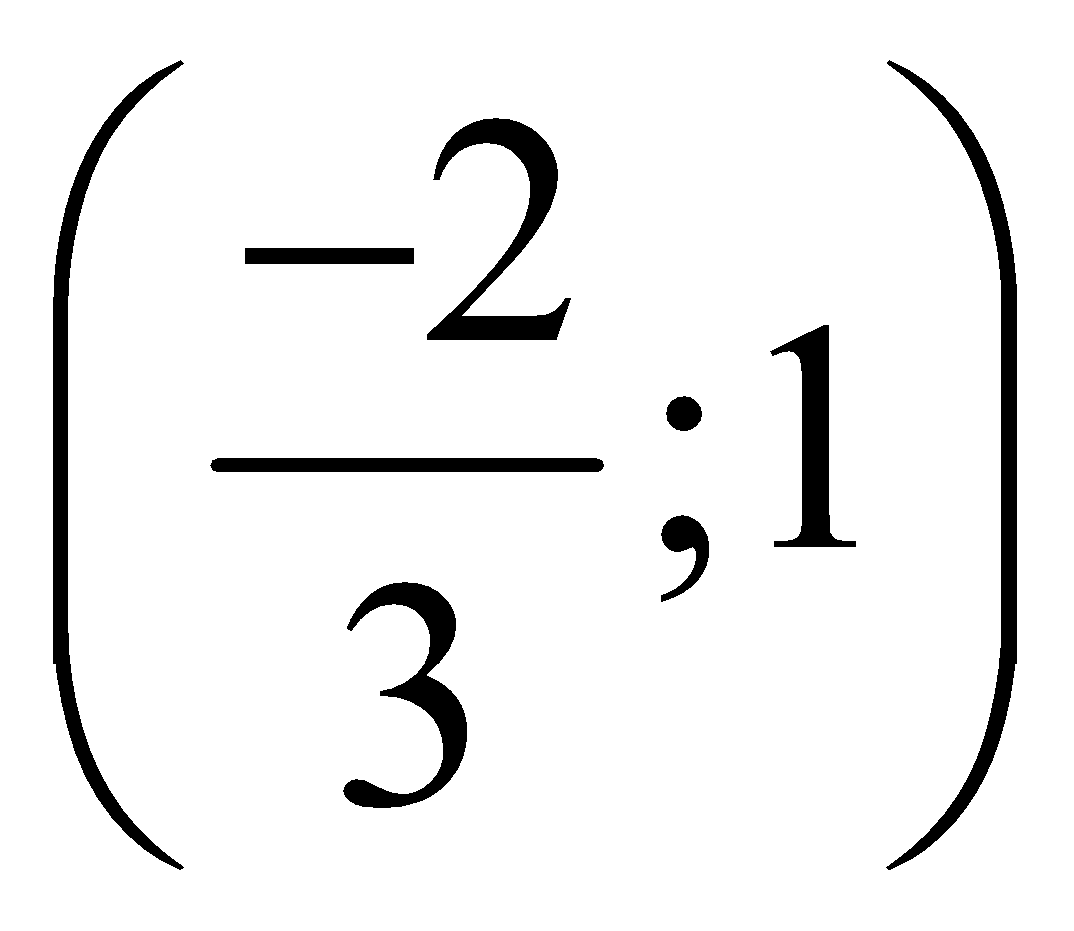
C.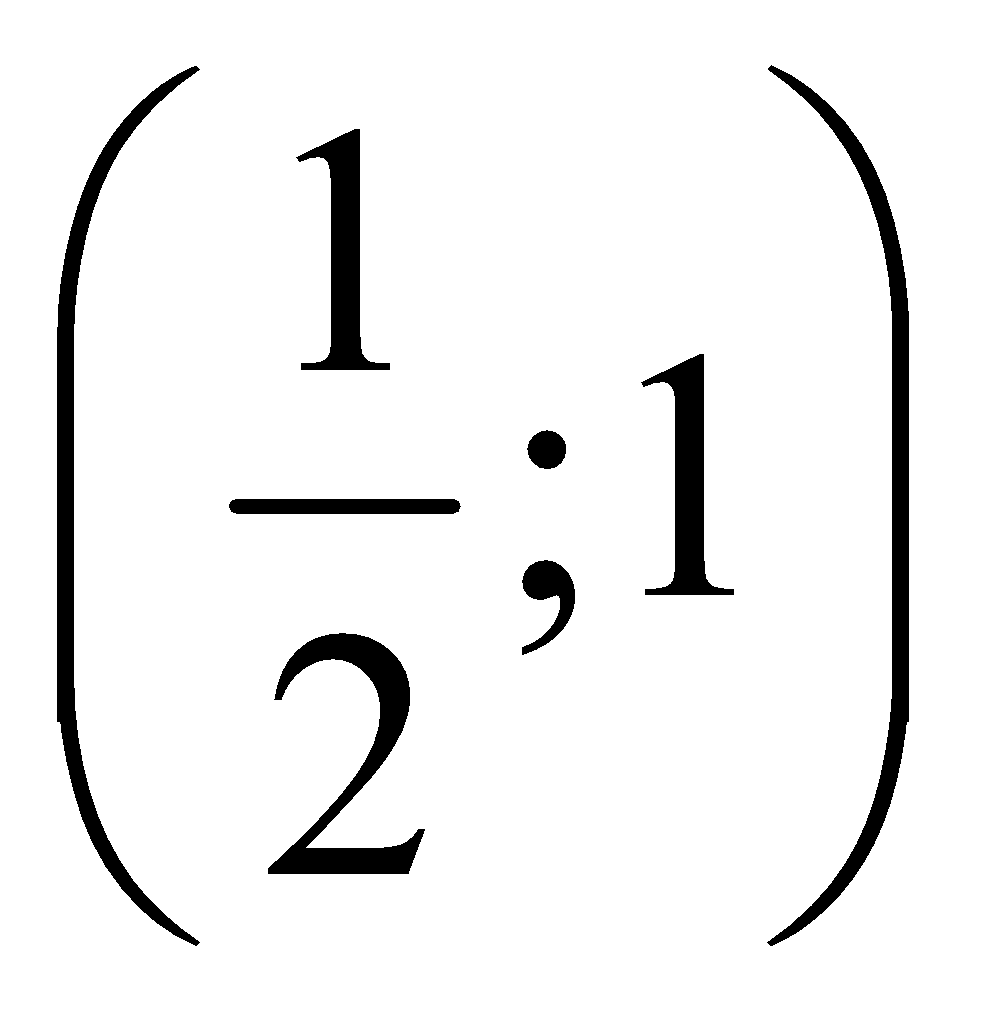
D. (-∞; +∞)
Một nhà dịch tế học xác định được rằng t tuần sau khi khởi phát 1 loại dịch bệnh, số ca nhiễm mới đc phát hiện là N(t) = 16+t2 trâm ca. Thời điểm nào dịch diễn biến xấu nhất?
A. T= 6 tuần sau
B. T= 4 tuần sau
C. T = 5.5 tuần sau
D. T= 4.5 tuần sau
lim![]()
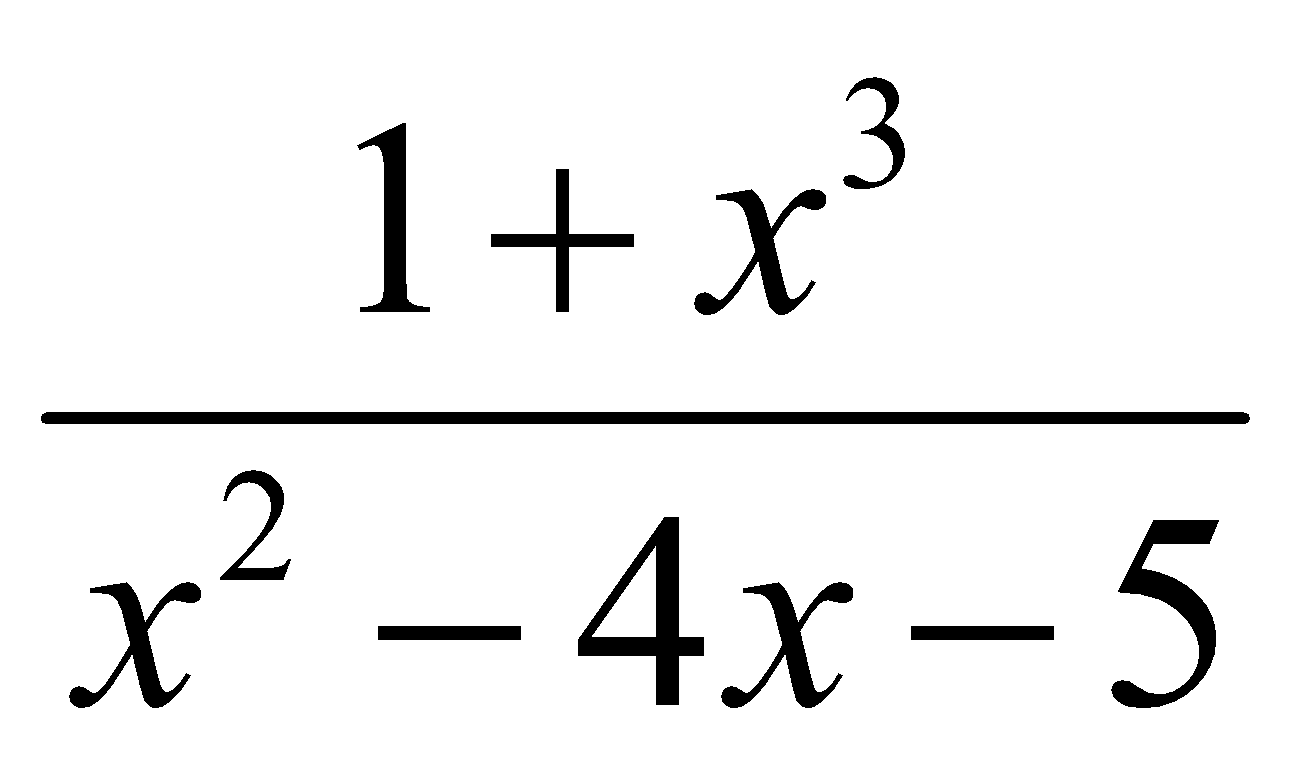 =
=
A. ![]()
B. 0
C. ![]()
D. +![]()
Phương trình tiếp tuyến với đồ thị điểm hàm số f(x) = 3x²(2√x + 5)√x tại (c;f(c)) với c=1 là
A. Y= 45x-24
B. Y=-34x+12
C. Y=-45x+24
D. Y=-3x+8
Mức lương khởi điểm của Gray là 55, 000và anh ấy được tăng thêm 1000 mỗi năm. Viết công thức hàm tốc độ thay đổi tương đối của mức lương của Gray theo thời gian
A. F(t) = 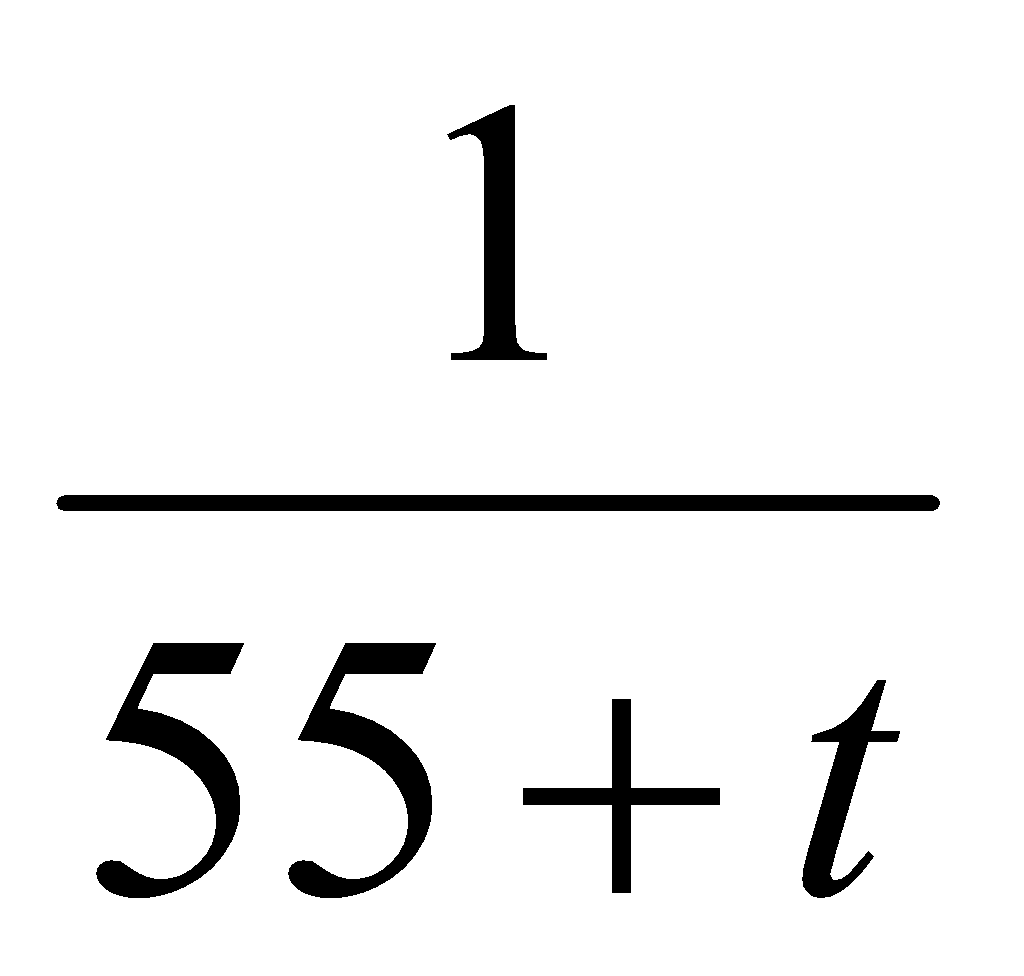
B. F(t) = 1000t
C. F(t) = 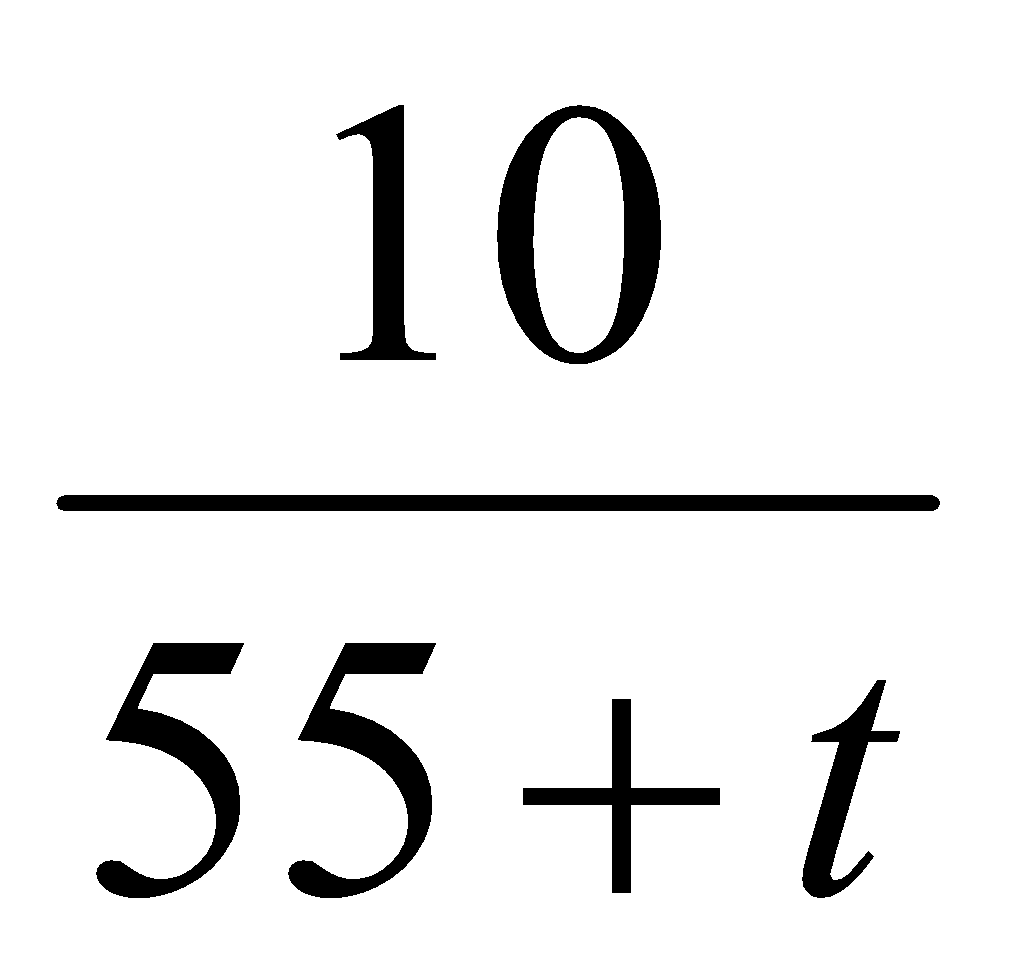
D. F(t) =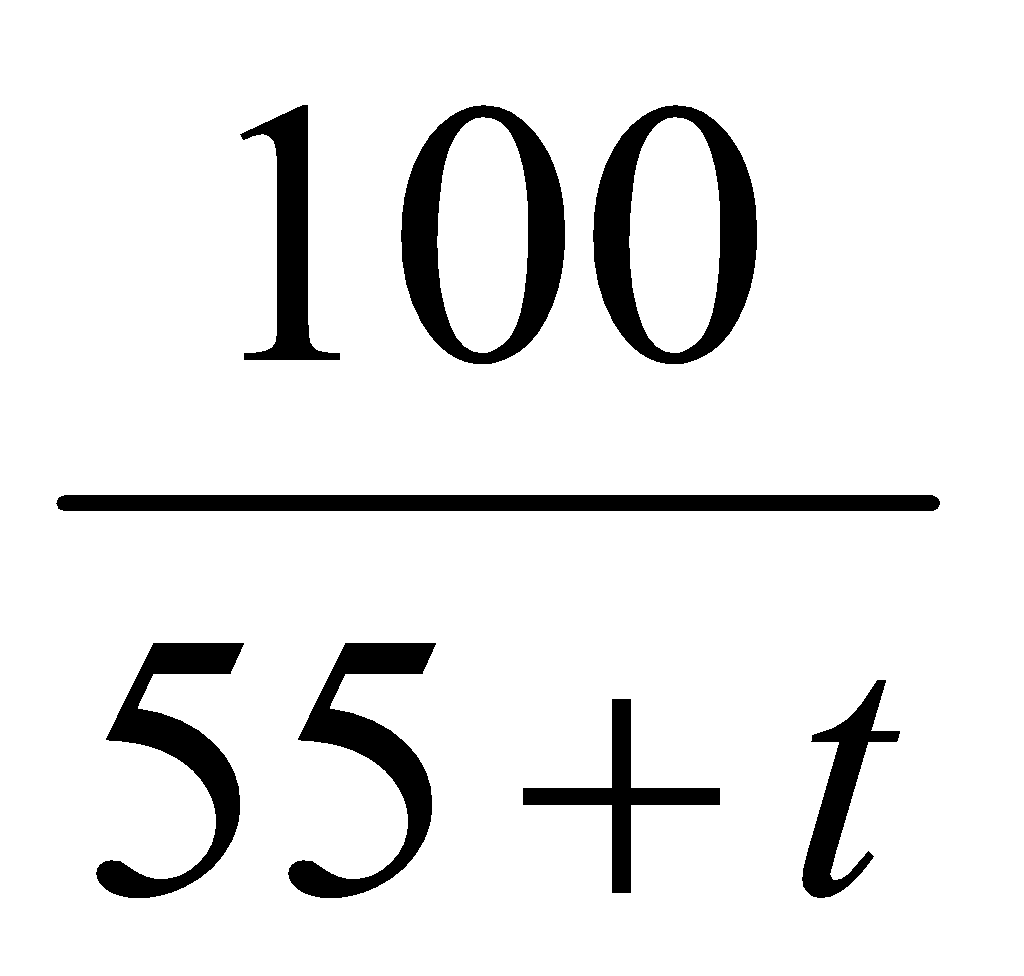
Một chiếc hộp kín dạng hình hộp chữ nhật, đáy hình vuông có thể tích là 200m³. Vật liệu để làm nắp và đáy có giá $5 mỗi m2 và vật liệu để làm mặt bên có giá $4 mỗi m². Khi đó công thức tổng diễn tổng chi phí C để làm chiếc hộp đó theo đô dài canh đáy X là
A. C= 10x2 +![]()
B. C= 2x2 + 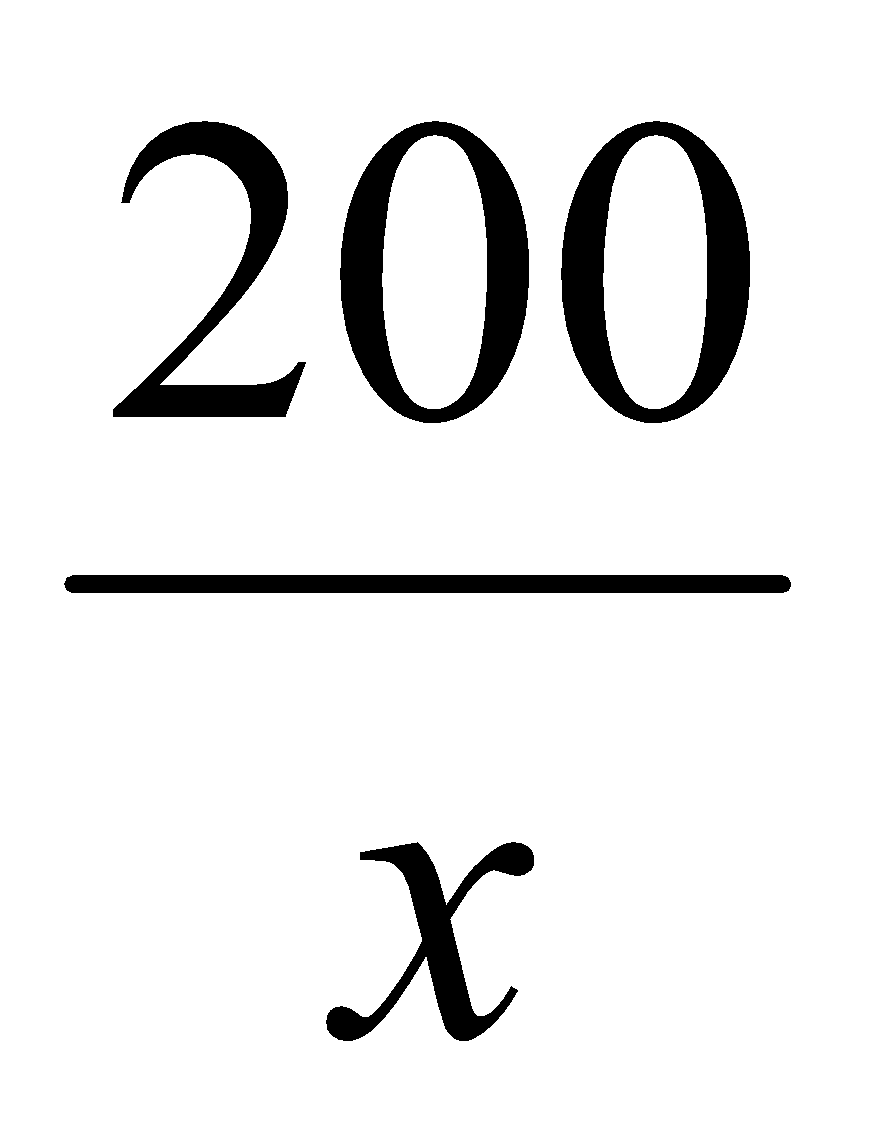
C. C= 2x2 + ![]()
D. C= 10x2 + ![]()
chi phí cận biên của một nhà máy là 9(q-3)2 đôla mỗi đơn vị khi mức sản xuấtlà q đơn vị. Biết rằng chi phí cố định ( chi phí tại mức sản lượng bằng 0) là $19. Chi phí để sản xuất13 đơn vị là:
A. $3100
B. $31
C. $31000
D. $310
Hàm số f(x) = 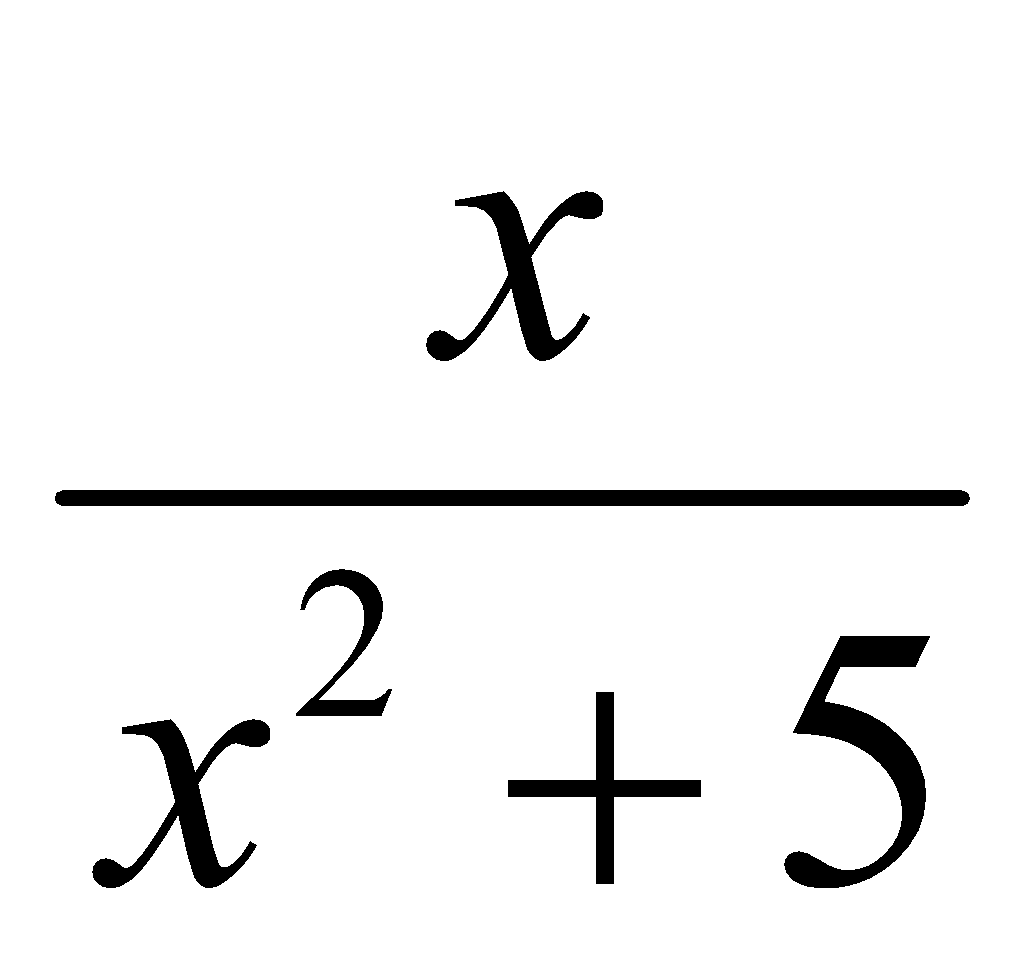 đạt cực tiểu tương đối tại:
đạt cực tiểu tương đối tại:
A. x = ![]()
B. x = -![]()
C. x = 1
D. x = 0
Số dân của .một thành phố đc tính bởi công thức P= Aekt trong đó P là dân số tại thời điểm t, A là dân số tại thời điểm ban đầu và k là tốc độ tăng trưởng bình quân đầu người. Giả sử số dân ban đầu của thành phố là 10 triệu ng và tốc độ tăng trưởng bình quân 2%. Hỏi sau 10 năm dân số đạt xấp xỉ bao nhiêu
A. 32.2140 triệu
B. 122.1400 triệu
C. 22.2140 triệu
D. 12.2140 triệu
Hệ số chặn y của đồ thị hàm số f(x) = ![]()
A.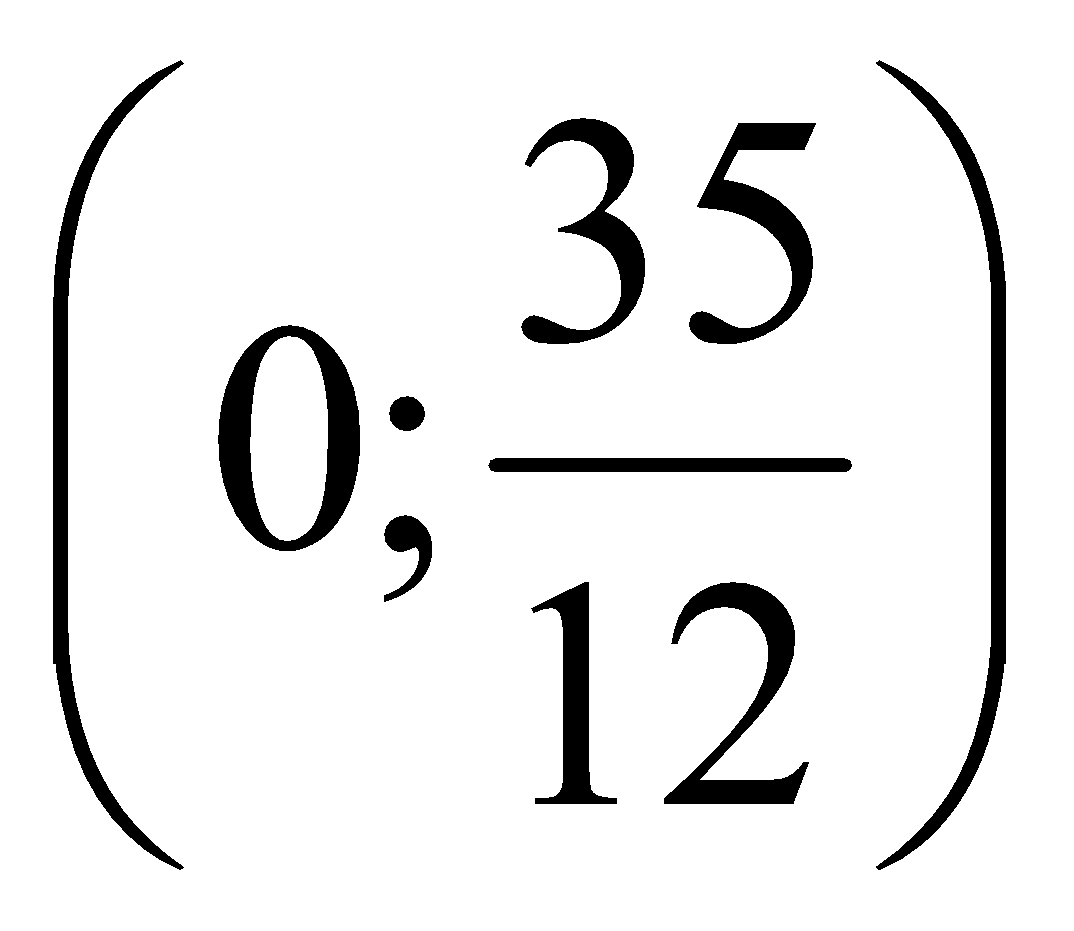
B. (-3;0)
C. (-5;0) và (-7;0)
D. (5;0) và (7;0)
Cho y là hàm khả vi của x được xác định bởi 2x + (x2+1)y + y3 = 0. Khi đó ![]() =
=
A. 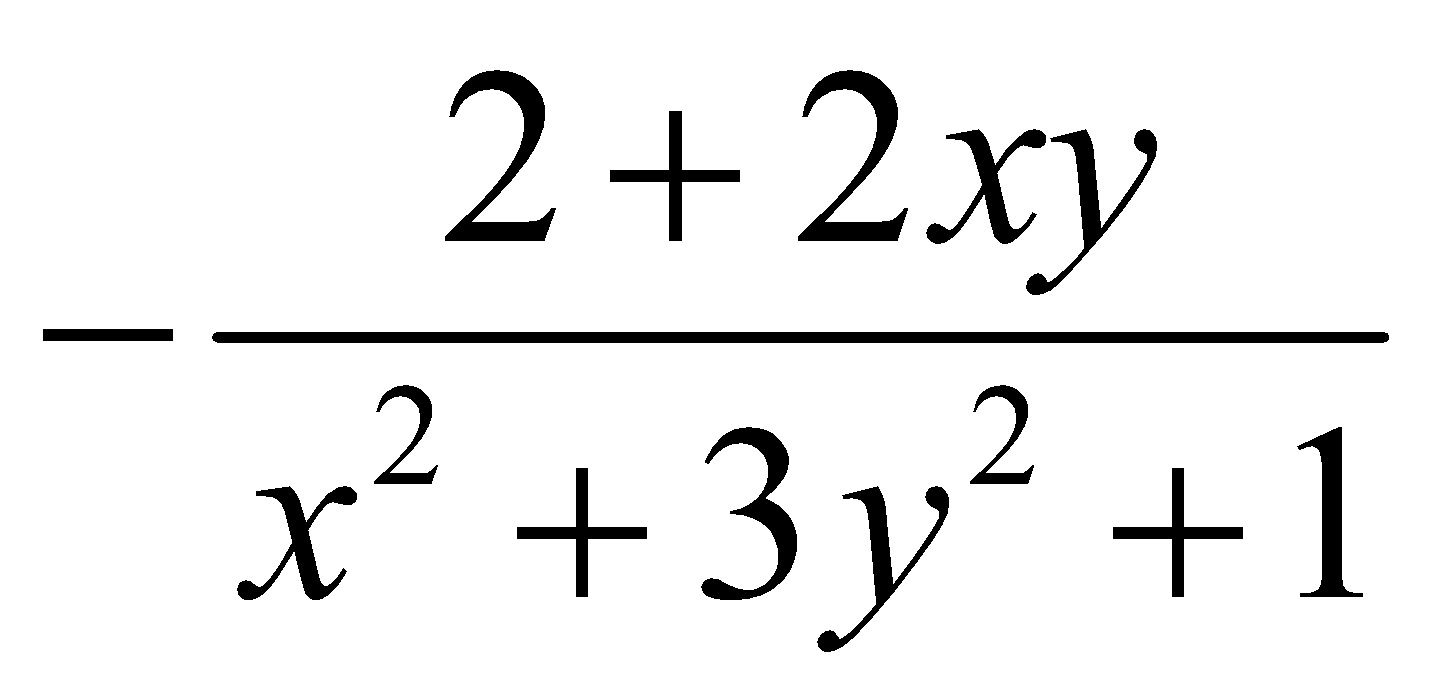
B. ![]()
C.![]()
D.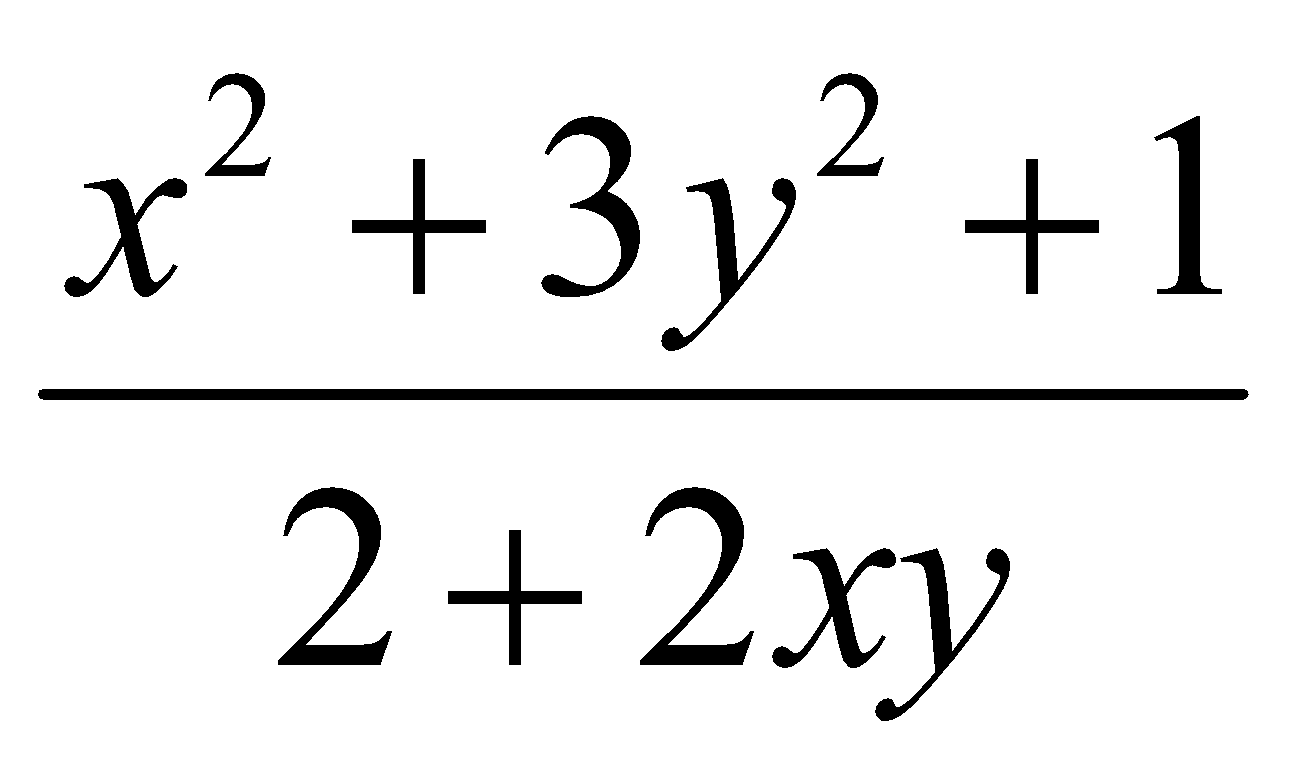
Quản lý của 1 hãng sản xuấtthiết bị ước tính rằng tỷ lệ các thiết bị còn hoạt động sau t tháng đc cho bởi tích phân: 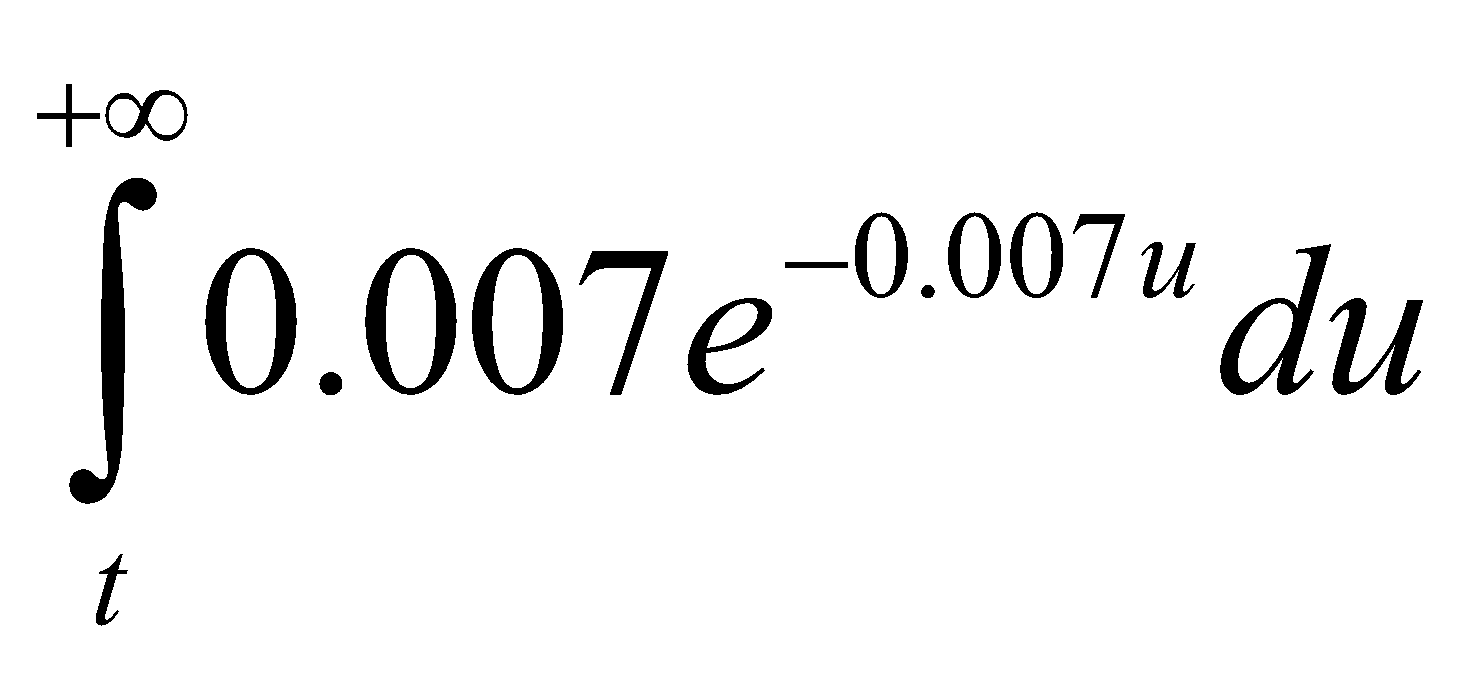
Tỷ lệ các thiết bị còn hoạt động sau 3 năm là:
A. 0.532
B. 0.777
C. 0.681
D. 0.468
Một doanh nghiệp sản xuất2 lọai sản phẩm kết hợp với hàm chi phí là TC=3Q12+ 2Q22 + 2Q1Q2 +200. Giá bán sản phẩm hàng hóa thứ 1 và 2 lần lượt là à 72 và 54. Khi đó hàm lợi nhuận của doanh nghiệp là:
A. π= 72Q1 +54Q2 – (3Q12+ 2Q22 + 2Q1Q2 +200)
B. π= 72Q1 +64Q2 +3Q12+ 2Q22 + 2Q1Q2 +200
C. π= 72Q1 -64Q2 – 3Q12+ 2Q22 + 2Q1Q2 +200
D. π= 64Q1 +72Q2 – 3Q12- 2Q 22- 2Q1Q2 -200
Sau khi giải bài toán “Tìm cực đại của hàm số S(x;y) = 12x+49y, x>0, y>0 với điều kiện x2+7y2=487” bằng phương pháp nhân tử Lagrange nếu ta thay điều kiện bài toán thành x2+7y2=488 thì cực đại hàm số sẽ
A. tăng xấp xỉ 11,3 đơn vị
B. tăng xấp xỉ 0,5 đơn vị
C. giảm xấp xỉ 4,5 đơn vị
D. giảm xấp xỉ 0,5 đơn vị
Cho hàm số g(x) thảo mãn g(0)=-1 và g’(0)=2 và hàm số f(x)= (2x+g(x))3. Khi đó f’(0)=
A. 12
B. 32
C. 21
D. -12
Khi một loại sản phẩm có giá p đôla mỗi đơn vị thì cầu đối với sản phẩm đó là q=180-2p2 đơn vị. Ở mức giá nào sau đây cầu không co giãn
A. 7$
B. 5$
C. 8$
D. 6$
Một nhà sản xuất ước tính khi x đươn vị hàng hóa được sản xuất thì tổng chi phí sản xuất sẽ là C(x)=x4-4x3+690x+4500 đôla. Khi đó chi phí cận biên khi sản xuất 20 đơn vị hàng hóa là
A. 37890
B. 27890
C. 17890
D. 57890
Cho hàm số z=f(x;y) có các đạo hàm riêng cấp một fx=3x+2y-7/2; fy = 2x-y2. Hàm số có 1 điểm tới hạn là
A. 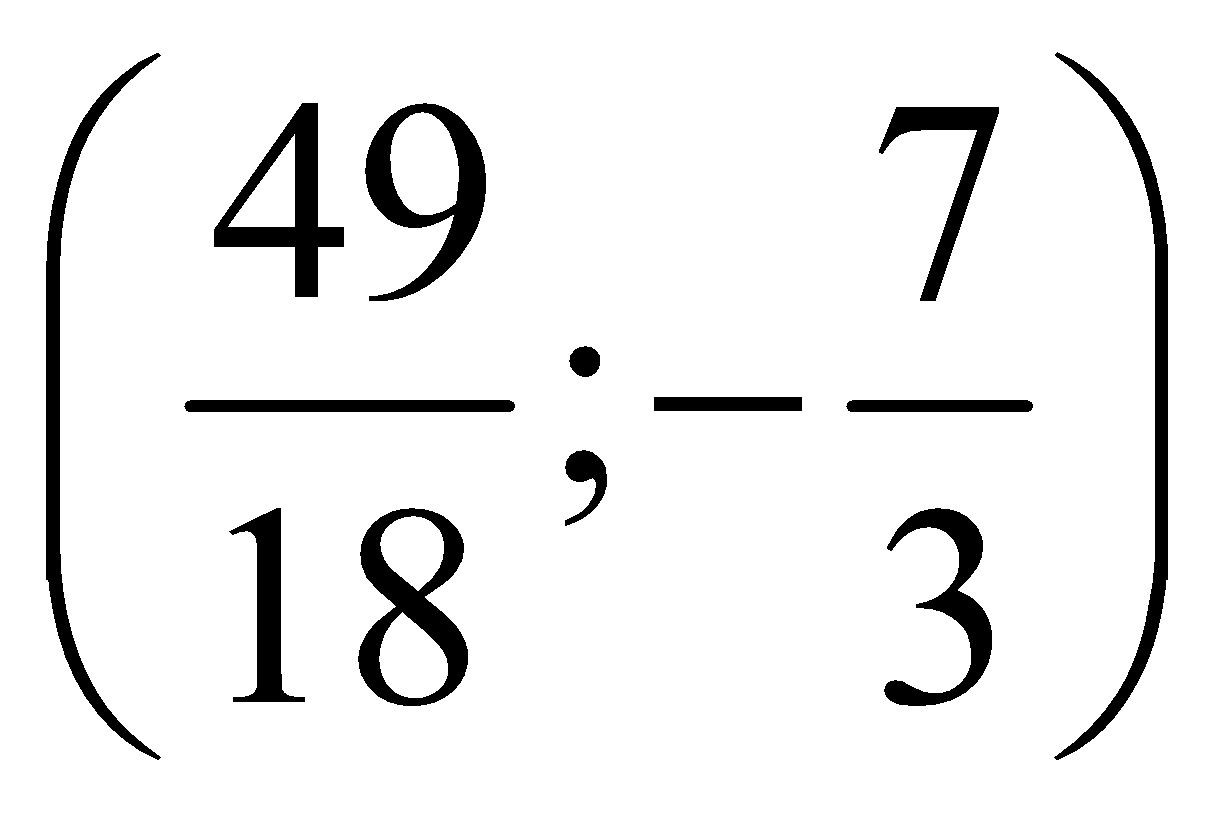
B. (![]()
C. (2;2)
D. (![]()
Người ta ước tính rằng t năm sau kể từ đầu năm 2012 lượng cầu đối với dầu của 1 quốc gia thay đổi với tốc độ D’(t) = (2+3t)-1 tỷ thùng/năm. Lượng dầu tiêu thụ trong năm 2014 nhiều hơn 2013 bao nhiêu thùng
A. 0.8047 tỷ thùng
B. 0.1567 tỷ thùng
C. 0.1118 tỷ thùng
D. 0.3466 tỷ thùng
Quản lý 1 cửa hàng tạp hóa cung cấp 2 nhãn hiệu thức ăn cho mèo, nhãn hiệu A có chi phí 24 cents mỗi hộp và nhãn hiệu B có chi phí 18 cents mỗi hộp. Nếu bán nhãn hiệu A với giá x cents mỗi hộp nhãn hiệu B y cents mỗi hộp thì mỗi ngày sẽ bán đc 74-6x+4y hộp A và 98+3x-7y hộp B. Hàm biểu diễn tổng lợi nhuận hàng ngày là
A. (74-6x+4y)x+(98+3x-7y)y
B. (74-6x+4y)(x-18)+(98+3x-7y)(y-24)
C. 40(74-6x+4y) + 18(98+3x-7y)
D. (74-6x+4y)(x-24)+(98+3x-7y)(y-18)
Cho hàm cầu D(q)=40e-0.05q đôla mỗi đơn vị. Tổng lượng tiền mà ng tiêu dùng sẵn lòng chi tiêu để có 10 đơn vị hàng hóa đó là
A. WS= 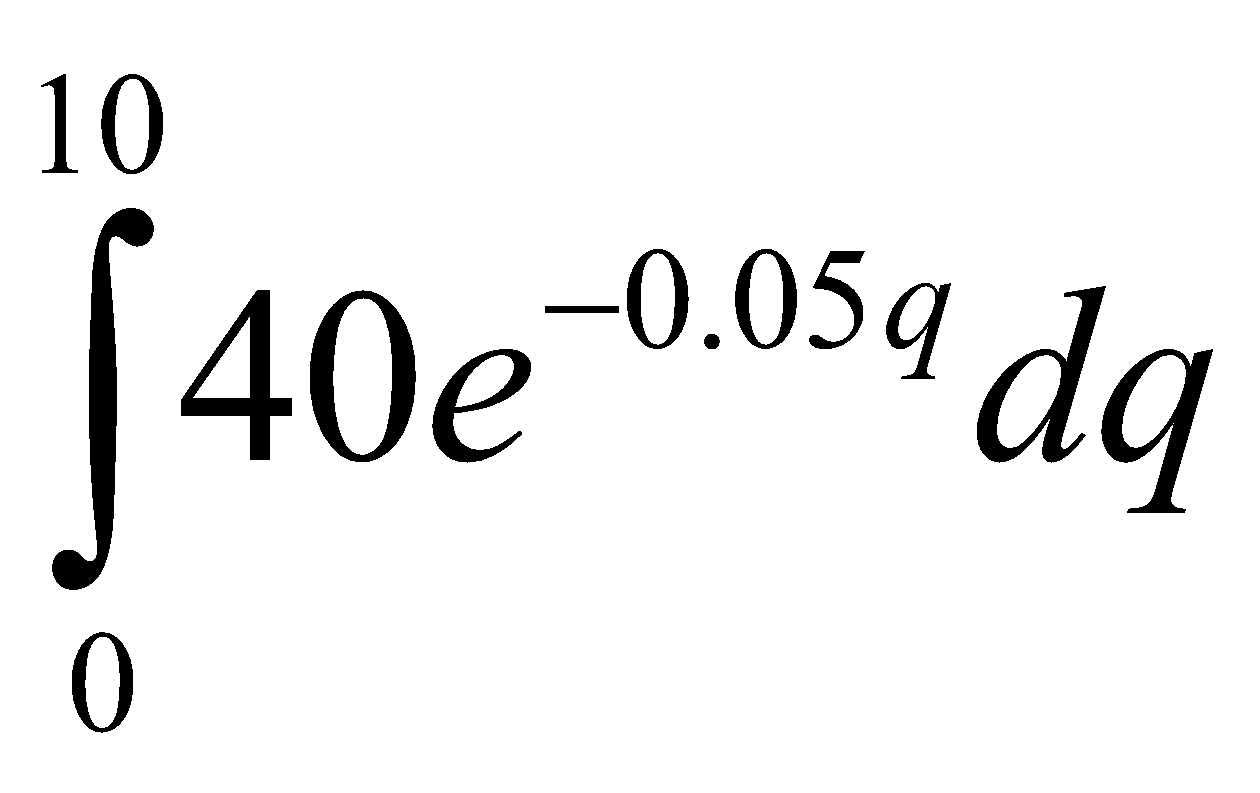
B. WS=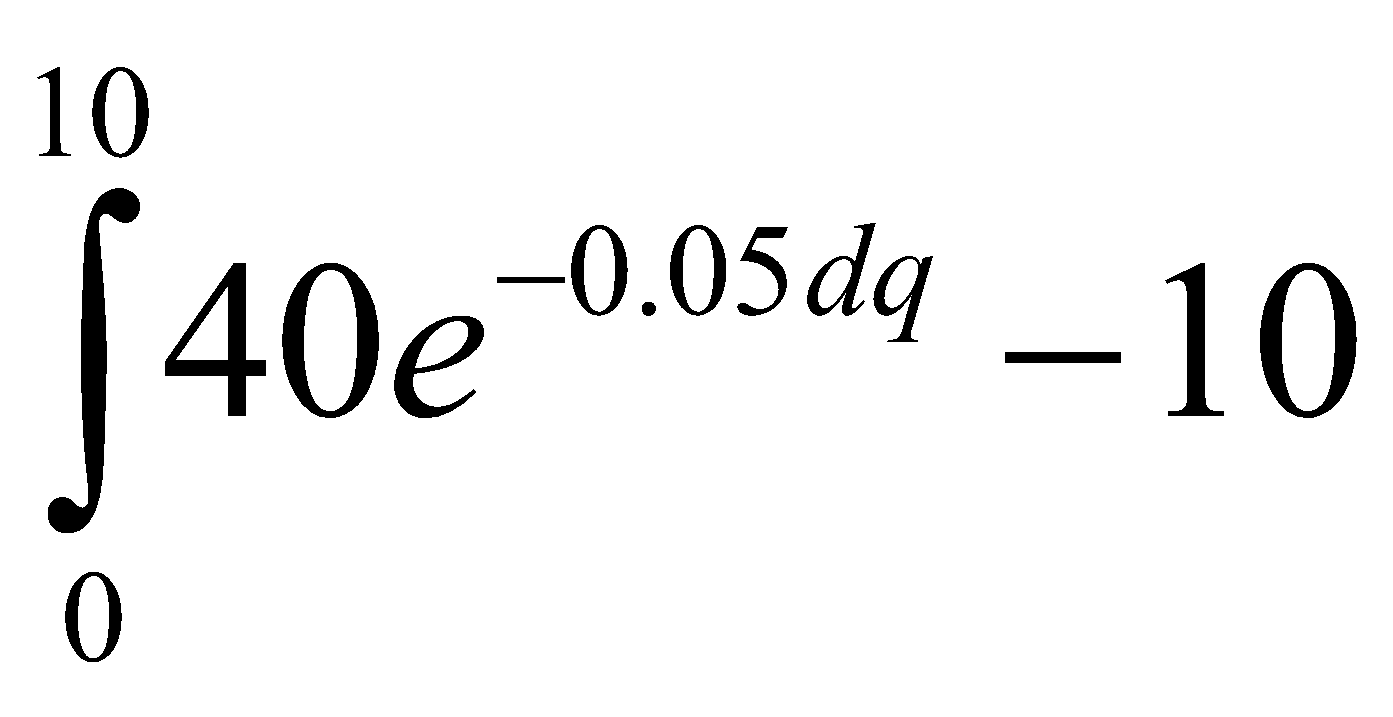
C. WS=10 -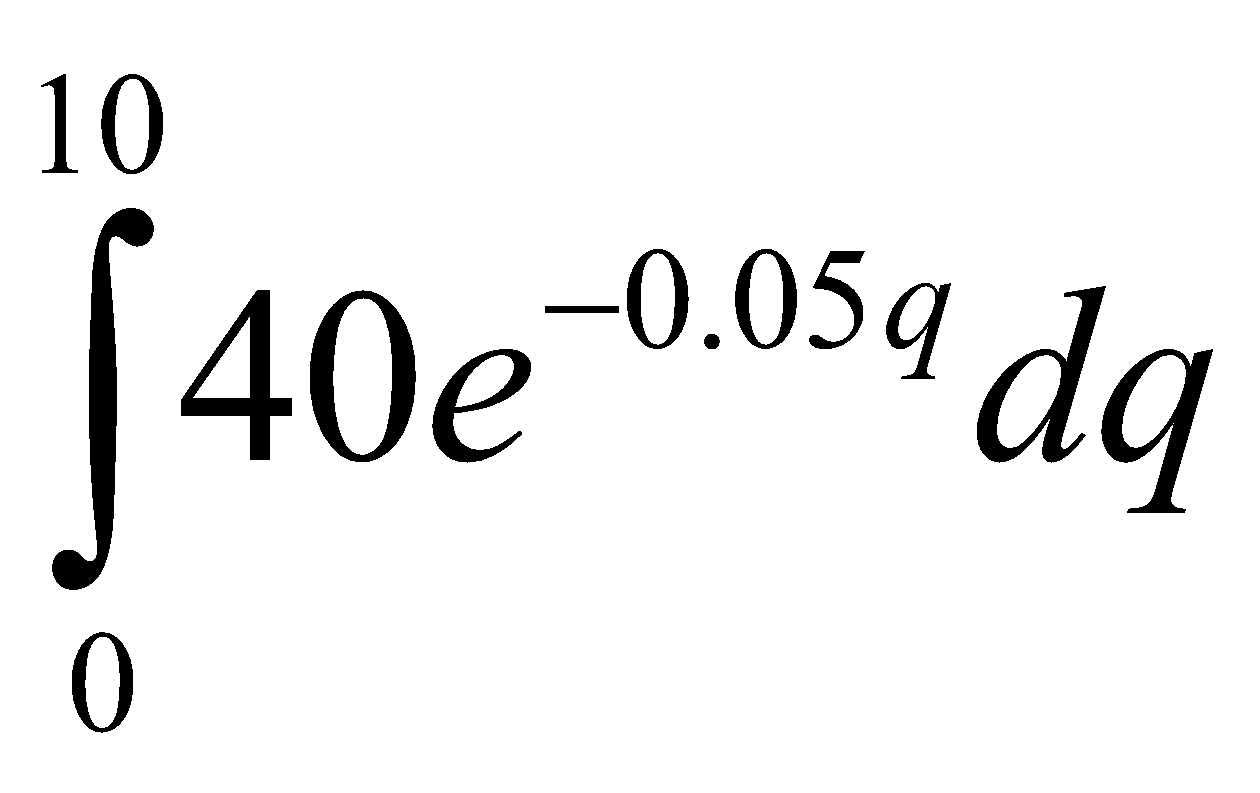
D. WS=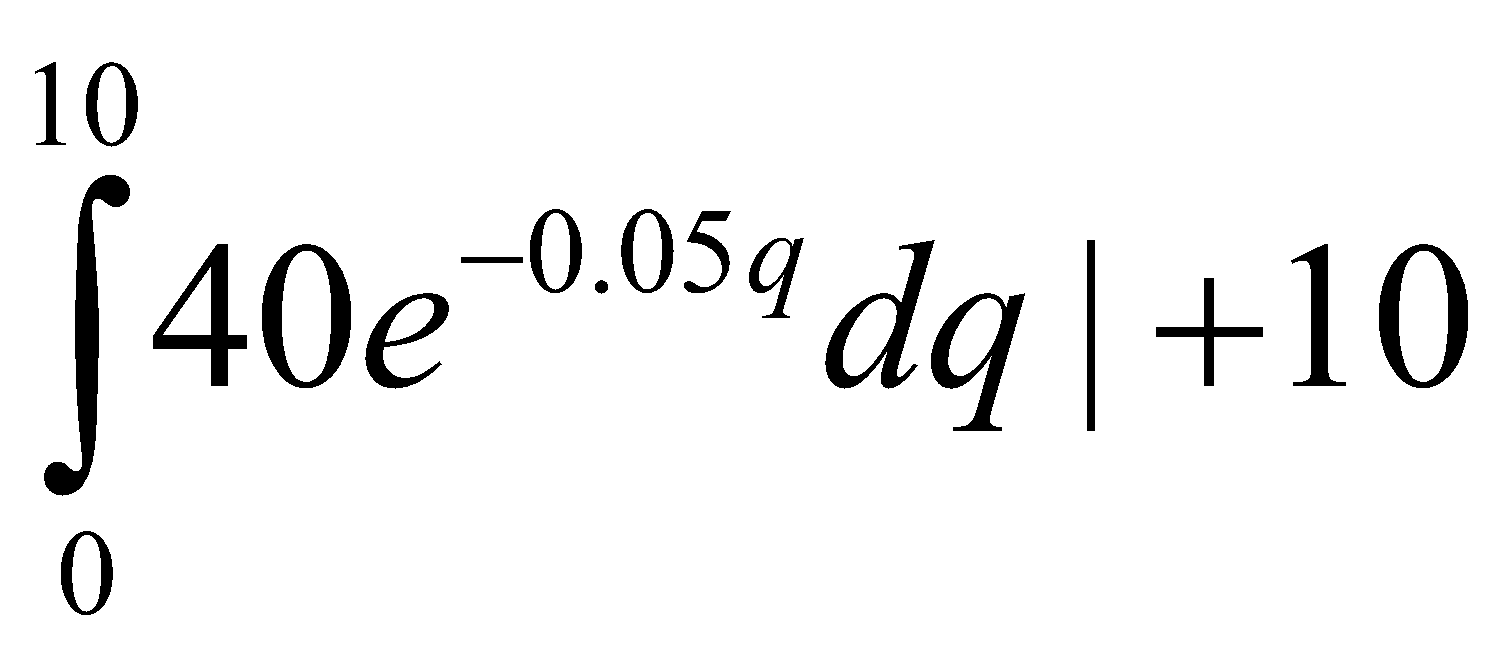
Cho hàm số f(u;v) = ln(v2 +2u2). Đạo hàm riêng cấp 2 hỗn hợp của f là:
A. 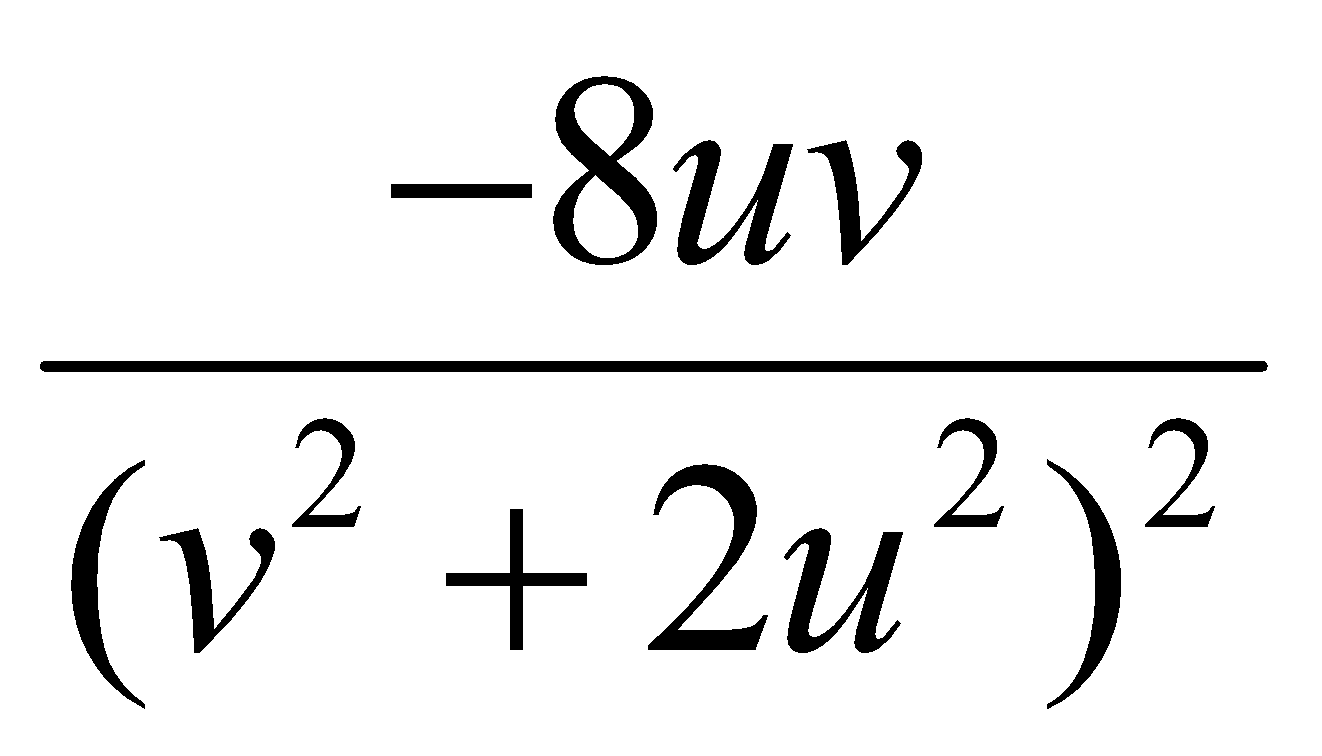
B.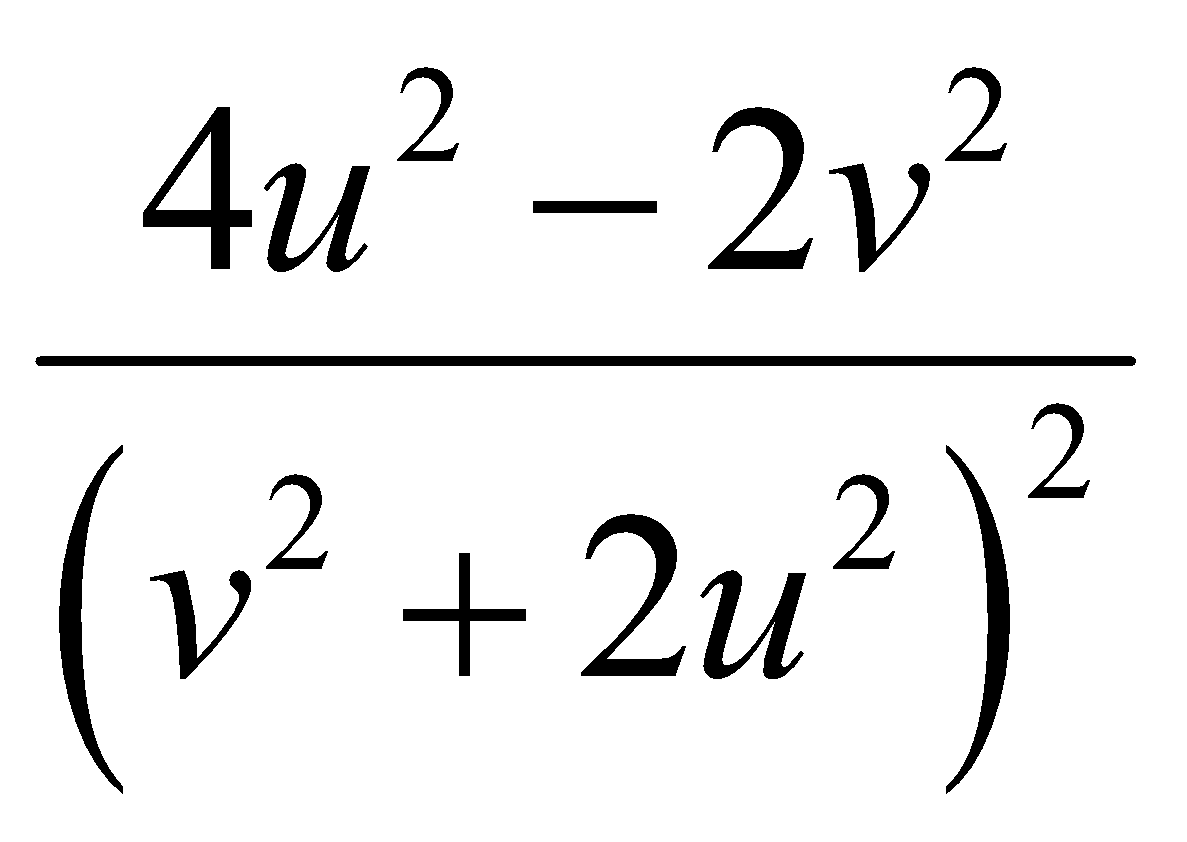
C.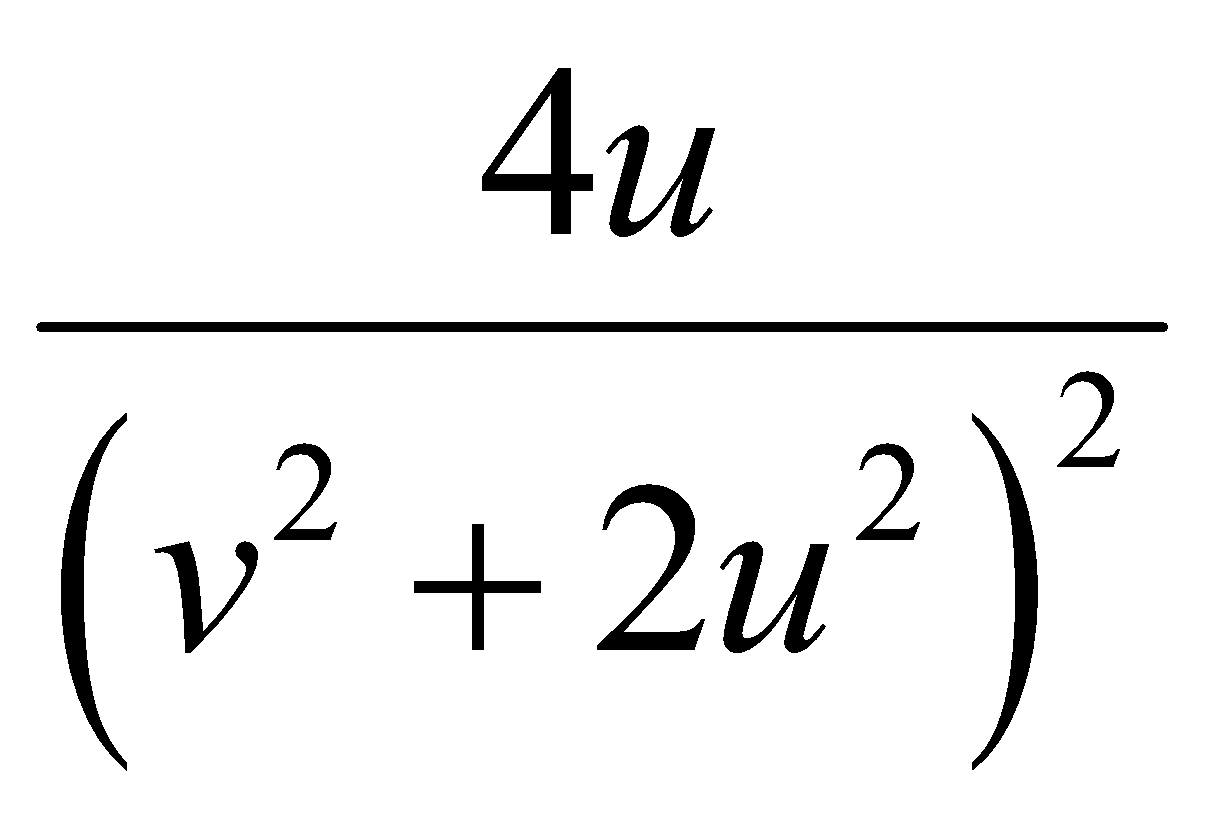
D.