Quiz

100 câu trắc nghiệm Số phức nâng cao (P3)

Admin25 câu hỏiToánLớp 12

Bắt đầu ngay

25 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.

A. Đường tròn ( x - 2) ²+ ( y + 2) ²= 100.

B. Elip

C. Đường tròn ( x -2) ²+ ( y + 2) ²= 10.

D. Elip

2. Nhiều lựa chọn

Cho số phức z thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z là?

C. ( x + 2) ²+ ( y - 2) ²= 64.

D. ( x + 2) ²+ ( y - 2) ²= 8.

3. Nhiều lựa chọn

Tìm nghiệm của phương trình:

B. Không có z thỏa mãn

4. Nhiều lựa chọn

Tìm nghiệm của phương trình: ( z + 3 - i)²- 6( z + 3 - i) + 13 = 0

A. z = 3i; z = 1 - 2i

B. z = - i; z = 3i + 4

C. z = 3i + 4; z = 3i

D. z = 3i; z = -i

5. Nhiều lựa chọn

Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| $\bar{z}$ + 2 + 4i| và $\frac{z - i}{\bar{z} + i}$ là số thuần ảo.

6. Nhiều lựa chọn

Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa mãn là đường tròn C. Diện tích S của đường tròn C bằng bao nhiêu?

A. S = 4π.

B. S = 2π.

C. S = 3π.

D. S = π.

7. Nhiều lựa chọn

Tính giá trị của biết z₁; z₂; z₃; z₄ là nghiệm phức của phương trình ( 5z²- 6iz - 2)( -3z²+ 2iz) = 0.

A. 12/25

B. 13/45

C. 11/23

D. 26/7

8. Nhiều lựa chọn

Tính mô-đun của số phức z, biết và z có phần thực dương.

A. 2

B. 1

C.3

D. $\sqrt{5}$

9. Nhiều lựa chọn

Giải phương trình sau: ( z²+ z) ²+ 4( z²+ z) - 12 = 0

A. z = -1; z = 2

10. Nhiều lựa chọn

Giải phương trình sau: ( z²+ 3z + 6) ²+ 2z( z²+ 3z + 6) - 3z² = 0

D. Cả A và C đúng

11. Nhiều lựa chọn

Cho phương trình: ( z²- z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.

A. -1

B. -2

C. -3

D. -4

12. Nhiều lựa chọn

Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z₁= 1 + 2i; z₂= -2 + 5i ; z₃= 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là

A. -1 + 7i.

B. 5 + i.

C. 1 + 5i.

D. 3 + 5i.

13. Nhiều lựa chọn

Cho 3 điểm A ; B ;C lần lượt biểu diễn cho các số phức z₁; z₂; z₃ .Biết | z₁| = | z₂| = | z₃| và z₁+ z₂= 0 . Khi đó tam giác ABC là tam giác gì?

A. Tam giác ABC đều.

B. Tam giác ABC vuông tại C.

C. Tam giác ABC cân tại C.

D. Tam giác ABC vuông cân tại C.

14. Nhiều lựa chọn

Xét số phức z thỏa mãn 2|z - 1 | + 3| z - i | $\leq 2 \sqrt{2}$ . Mệnh đề nào dưới đây đúng?

15. Nhiều lựa chọn

Đẳng thức 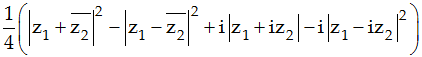bằng

A. z₁/z₂

B. z₁z₂

C. z₁+ z₂

D. z₁- z₂

16. Nhiều lựa chọn

Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thoả mãn điều kiện: là hình gì?

A. Một đường thẳng.

B. Một đường Parabol.

C. Một đường Elip.

D. Một đường tròn.

17. Nhiều lựa chọn

Cho số phức z = m - 2 + ( m²- 1) i với m là số thực. Gọi (C) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Tính diện tích hình phẳng giới hạn bởi (C) và Ox.

A. 1.

B. 4/3.

C. 32/3.

D. 8/3.

18. Nhiều lựa chọn

Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| = | 2 $\bar{z}$ - z + 3i | . Tập hợp tất cả những điểm M như vậy là

A. một parabol.

B. một đường thẳng.

C. một đường tròn.

D. một elip.

19. Nhiều lựa chọn

Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện