10 câu hỏi
Cho (O; 4) có dây AC bằng cạnh hình vuông nội tiếp và dây BC bằng cạnh tam giác đều nội tiếp đường tròn đó (điểm C và A nằm cùng phía với BO). Tính số đo góc ACB.
30°.
45°.
60°.
15°.
Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm (O), đường kính AM. Góc BAH bằng
góc AMC.
góc ABH.
góc ACM.
góc OCA.
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O; 4). Biết rằng AC = 4 cm. Lấy D là điểm bất kì khác A, B, C trên đường tròn. Chọn khẳng định đúng.
\[\widehat {BDA} = 90^\circ \].
\[\widehat {BCA} = 30^\circ \].
\[\widehat {CDA} = 30^\circ \].
\[\widehat {CBA} = 60^\circ \].
Cho đường tròn như hình vẽ dưới đây. Biết rằng, CA = CD, \[\widehat {BDA} = 26^\circ ,\]\[\widehat {ACD} = 28^\circ \]. Số đo góc BAC là
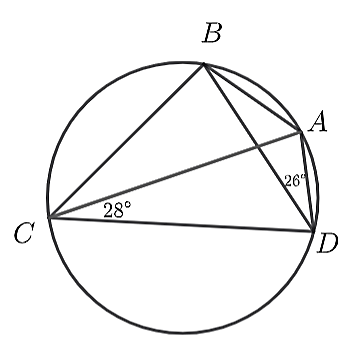
90°.
80°.
50°.
100°.
Cho đường tròn tâm O và hai dây cung AB // CD. Trên cung AB lấy điểm M. Chọn khẳng định đúng trong các khẳng định dưới đây.
\[\widehat {AMC} = \widehat {BMD}\].
\[\widehat {AMB} = \widehat {CMD}.\]
\[\widehat {AMC} = \widehat {AMB}.\]
\[\widehat {BMA} = \widehat {BMD}.\]
Cho đường tròn tâm O, đường kính AC. Lấy B ∈ (O) sao cho \[\widehat {ACB} = 70^\circ \]. Kẻ BD ⊥ AC (D ∈ (O)). Số đo \[\widehat {CDB}\] là
20°.
30°.
10°.
40°.
Qua điểm A nằm ngoài đường tròn (O) kẻ hai cát tuyến ABC và ADE với đường tròn đó (B nằm giữa A và C, D nằm giữa A và E). Kẻ dây BF // DE. Chọn khẳng định sai trong các khẳng định sau.
\[\widehat {DBF} = \widehat {BCE}.\]
\[\widehat {BDC} = \widehat {BFC}.\]
\[\widehat {DBF} = \widehat {DCF}.\]
\[\widehat {DFB} = \widehat {FCD}.\]
Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D). Gọi F là một điểm trên đường tròn sao cho B nằm chính giữa cung DF, I là giao điểm của FA và BC. Biết \[\widehat E = 25^\circ \], số đo góc AIC là
20°.
50°.
25°.
30°.
Cho AB và CD là hai đường kính vuông góc với nhau của đường tròn (O; R). Qua điểm M thuộc cung nhỏ AC (M ≠ A, M ≠ E) kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E, F. Chọn khẳng định đúng trong các khẳng định sau.
\[\widehat {MFO} = 2\widehat {MBO}.\]
\[\widehat {MFO} = \frac{1}{2}\widehat {MBO}.\]
\[\widehat {MFO} = \widehat {MBO}.\]
\[\widehat {MFO} = 2\widehat {MOB}.\]
Cho đường tròn (O) đường kính BC cố định. Điểm A di động trên đường tròn khác B và C. Vẽ đường kính AD. Khi A ở vị trí mà diện tích tam giác ABC đạt giá trị lớn nhất thì góc ADC bằng
30°.
60°.
45°.
90°.
