32 câu hỏi
Giá trị của tham số \(m\) để hệ số góc của đường thẳng \(y = \left( {1 - m} \right)x + 3 + 2m\) bằng 5 là
\(m = - 5.\)
\(m = 6.\)
\(m = 1.\)
\(m = - 4.\)
Phương trình \(4x - 3y = - 1\) nhận cặp số nào dưới đây là một nghiệm?
\(\left( { - 1\,;\,\,1} \right)\).
\(\left( {1\,;\,\, - 1} \right).\)
\(\left( {1\,;\,\,1} \right).\)
\(\left( { - 1\,;\,\, - 1} \right).\)
Căn bậc hai số học của 4 bằng
\[ - 2.\]
\[ - 16.\]
16.
2.
Biểu thức \(\sqrt[3]{{{{\left( {\sqrt 2 - 3} \right)}^3}}}\) có giá trị là
3.
\(\left| {\sqrt 2 - 3} \right|.\)
\(\sqrt 2 .\)
\(\sqrt 2 - 3.\)
Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 2}\\{mx + y = 1}\end{array}} \right.\) (\(m\) là tham số) có nghiệm duy nhất khi
\(m \ne 1\).
\(m \ne - 1\).
\(m \ne 0\).
\(m \ne 2\).
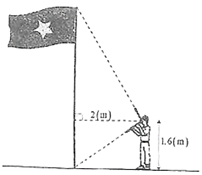
Một học sinh cầm thước êke đưng cách cột cờ 2 m . Bạn ấy lần lượt nhìn theo hai cạnh góc vuông của êke thì thấy ngọn và chân của cột cờ (tham khảo hình vẽ). Biết mắt học sinh cách mặt đất \(1,6\;{\rm{m}}\). Khi đó, chiều cao của cột cờ bằng
\(4,1\,\;{\rm{m}}{\rm{.}}\)
\(4,25\,\;{\rm{m}}{\rm{.}}\)
\(4,2\,\;{\rm{m}}{\rm{.}}\)
\(4,5\,\;{\rm{m}}{\rm{.}}\)
Thể tích của một quả bóng chuyền hơi có dạng hình cầu có đường kính bằng \[24{\rm{ cm}}\] là
\(2\,304\pi \,\,{\rm{c}}{{\rm{m}}^3}.\)
\(18\,432\pi \,\,{\rm{c}}{{\rm{m}}^3}.\)
\(576\pi \,\,{\rm{c}}{{\rm{m}}^3}.\)
\(768\pi \,\,{\rm{c}}{{\rm{m}}^3}.\)
Tam giác \[ABC\] vuông tại \(A\) có \(AC = 6\;\,{\rm{cm}}\,,\,\,BC = 12\,\;{\rm{cm}}\), số đo \(\widehat {ACB}\) bằng
\(60^\circ .\)
\(30^\circ .\)
\(45^\circ .\)
\(90^\circ .\)
Cho tam giác \[ABC\] vuông tại \(A\) có \(AB = 3\,\;{\rm{cm}}\,,AC = 4\,\;{\rm{cm}}\,,BC = 5\,\;{\rm{cm}}{\rm{.}}\) Khẳng định nào dưới đây đúng?
\(\sin C = \frac{3}{5}\).
\(\cos C = \frac{3}{4}\).
\(\tan C = \frac{4}{3}\).
\(\cot C = \frac{4}{5}\).
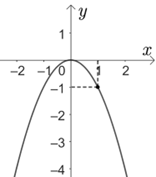
Hình vẽ dưới đây là của đồ thị hàm số nào?
\(y = {x^2}\).
\(y = - 2{x^2}\).
\(y = - {x^2}\).
\(y = 2{x^2}\).
Biết đường thẳng \(y = ax + b\,\,(a,\,\,b\) là tham số) đi qua điểm \(M\left( {2\,;\,\, - 1} \right)\) và song song với đường thẳng \(y = 2x - 7.\) Giá trị của biểu thức \(S = a - b\) bằng
\[ - 7.\]
\[ - 3.\]
7.
9.
Điều kiện xác định của biểu thức \(\sqrt {x - 2025} \) là
\(x < 2025\).
\(x \ge 2025\).
\(x > 2025\).
\(x \le 2025\).
Một hình nón có diện tích xung quanh bằng \(20\pi \,\,{\rm{c}}{{\rm{m}}^2}\) và độ dài đường sinh \(5\;\,{\rm{cm}}\,{\rm{.}}\) Bán kính đáy của hình nón đó là
\[5{\rm{ cm}}\,{\rm{.}}\]
\[4{\rm{ cm}}\,{\rm{.}}\]
\[3{\rm{ cm}}\,{\rm{.}}\]
\[6{\rm{ cm}}\,{\rm{.}}\]
Giá trị của biểu thức \(M = \sqrt 4 - \sqrt {16} \) bằng
6.
\[ - 2.\]
4.
\[ - 12.\]
Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ hai phương trình bậc nhất hai ẩn?
\(\left\{ {\begin{array}{*{20}{l}}{x - \sqrt y = 1}\\{x + 3y = 5}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x - 2{y^2} = 7}\\{2{x^2} - y = 4}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 6}\\{3x + 4y = 5}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x - \frac{1}{{2y}} = 3}\\{2x - 3y = 1}\end{array}} \right.\).
Cho tam giác \[ABC\] vuông tại \(A\). Khẳng định nào dưới đây đúng?
\(\sin B = \tan C\).
\(\frac{{AB}}{{AC}} = \frac{{\cos C}}{{\cos B}}\).
\(\sin B = \cos C\).
\(\tan B = \cos C\).
Cho đồ thị hàm số \(y = \left( {2a + 1} \right){x^2}\) (với \(a\) là tham số) đi qua điểm \(M\left( {1\,;\,\,2} \right)\). Giá trị của \(a\) là
\(a = \frac{1}{4}.\)
\(a = \frac{1}{2}.\)
\(a = 2.\)
\(a = - 2.\)
Đồ thị hàm số \(y = ax + b\) (\(a,\,\,b\) là tham số) đi qua hai điểm \(A\left( {1\,;\,\,3} \right)\,,\,\,B\left( {2\,;\,\,4} \right)\). Giá trị của \[a,\,\,b\] là
\(a = 2\,,\,\,b = 1\).
\(a = 2\,,\,\,b = 2\).
\(a = 1\,,\,\,b = 2\).
\(a = 1\,,\,\,b = 1\).
Đồ thị hàm số \(y = 2{x^2}\) đi qua hai điểm \[A\left( {\sqrt 2 \,;\,\,m} \right)\] và \[B\left( {\sqrt 3 \,;\,\,n} \right).\] Giá trị của biểu thức \(S = 2m - n\) là
\(S = 3\).
\(S = 2\).
\(S = 1\).
D. .
Cho tam giác \[ABC\] vuông tại \(A\), đường cao \(AH,AB = 3\;{\rm{cm}},AC = 4\;{\rm{cm}}\). Độ dài đoạn thẳng AH bằng
\(2,4\;\,{\rm{cm}}\).
\[1,4\;\,{\rm{cm}}.\]
\(\sqrt {12} \;{\rm{cm}}\).
\(\frac{{12}}{7}\;{\rm{cm}}\).
Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 3}\\{x - y = 1}\end{array}} \right.\) có nghiệm là
\(m = - 5\).
\(m = 6\).
\(m = 1\).
\(m = - 4\).
Phương trình \(4x - 3y = - 1\) nhận cặp số nào dưới đây là một nghiệm?
\(\left( {1\,;\,\,2} \right)\).
\(\left( {0\,;\,\, - 1} \right)\).
\(\left( {2\,;\,\,1} \right)\).
\(\left( {3\,;\,\,2} \right)\).
Cho tam giác \[ABC\] vuông tại \(C,\,\,CH \bot AB\,\,\left( {H \in AB} \right),\,\,AH = 16\,\;{\rm{cm}},\,\,HB = 9\,\;{\rm{cm,}}\)diện tích tam giác \[ABC\] bằng
\(72\,\;{\rm{c}}{{\rm{m}}^2}.\)
\(120\;\,{\rm{c}}{{\rm{m}}^2}.\)
\(150\,\;{\rm{c}}{{\rm{m}}^2}.\)
\(54\;\,{\rm{c}}{{\rm{m}}^2}.\)
Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{\frac{2}{x} + \frac{3}{y} = 5}\\{\frac{3}{x} - \frac{2}{y} = - 12}\end{array}} \right.\) là
\((2; - 3)\)
\(( - 2;3)\).
\(\left( { - \frac{{46}}{5}; - \frac{{39}}{5}} \right)\).
\(\left( { - \frac{1}{2};\frac{1}{3}} \right)\).
Cho hàm số \(y = - 3{x^2}\). Khẳng định nào sau đây đúng?
Hàm số nghịch biến trên \(\mathbb{R}\).
Hàm số nghịch biến khi \(x > 0\), đồng biến khi \(x < 0\).
Hàm số nghịch biến khi \(x < 0\), đồng biến khi \(x > 0\).
Hàm số đồng biến trên \(\mathbb{R}\).
Tại \(x = 10\) giá trị của biểu thức \(\sqrt {x - 1} + \sqrt {x + 6} \) bằng
5.
7.
10.
25.
Cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 1}\\{y = \frac{{ - 1}}{2}}\end{array}} \right.\). Giá trị của biểu thức \(\frac{1}{2}x_0^2 - 2y\) bằng
3.
1.
2.
0.
Tìm \(a\) và \(b\) để \(\left( {x\,;\,\,y} \right) = \left( {1\,;\,\,1} \right)\) là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ax + y = 2}\\{3x + by = 5}\end{array}} \right.\).
\(a = - 1\,,\,\,b = 2.\)
\(a = - 1\,,\,\,b = - 2\)
\(a = 1\,,\,\,b = - 2.\)
\(a = 1\,,\,\,b = 2\).
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5m - 1}\\{x - 2y = 2}\end{array}} \right.\) (\(m\) là tham số). Có bao nhiêu giá trị của \(m\) để hệ phương trình có nghiệm thỏa mãn: \({x^2} - 2{y^2} = - 2\)?
3.
0.
1.
2.
Cho đường thẳng \(d:y = - 2x - 4.\) Gọi \(A,\,\,B\) lần lượt là giao điểm của \(d\) với trục hoành và trục tung. Diện tích tam giác \(OAB\,\,(O\) là gốc tọa độ) bằng
3.
4.
2.
8.
Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(d:y = 7x - m - 7\) (\(m\) là tham số). Gọi \(S\) là tập tất cả các giá trị của \(m\) để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\) nằm bên phải trục tung sao cho trong các hoành độ \({x_A},{x_B}\) có ít nhất một hoành độ là số nguyên tố. Tổng tất cả các phần tử của \(S\) bằng
13.
10.
7.
8.
Số giá trị nguyên dương của tham số \(m\) để hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{mx - y = 3}\\{2x + my = 9}\end{array}} \right.\) có nghiệm duy nhất \(\left( {x\,;\,y} \right)\) sao cho \(A = 3x - y\) nhận giá trị nguyên là
1.
2.
3.
4.
