Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 4)

Hai bạn Minh và An xuất phát cùng một lúc từ địa điểm A để đi đến địa điểm B bằng phương tiện xe đạp điện. Mỗi giờ bạn Minh đi nhanh hơn bạn An 2km nên bạn Minh đến B sớm hơn bạn An 2,5 phút. Biết quãng đường AB dài 13km, tính vận tốc xe của mồi người. Hỏi Minh và An đi như vậy có đúng vận tốc quy định hay không nếu căn cứ theo quy định vận tốc tối đa của xe đạp điện là 25 km/h?

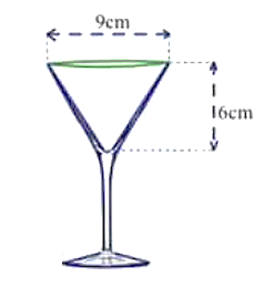Một ly rượu bằng thủy tinh phần đựng rượu dạng hình nón có đường kính miệng ly là 9 cm, chiều cao hình nón (như hình vẽ) là 6 cm. Hỏi ly đó có thể chứa đầy được bao nhiêu milliliter (ml) rượu? (Lấy $\pi \approx 3,14$ và coi độ dày thành ly là không đáng kể)

Giải hệ phương trình: $\left\{\begin{array}{l}\frac{2}{\left|x-1\right|}+3y=5\\ \frac{1}{\left|x-1\right|}-2y=-1\end{array}\right..$

Trên mặt phẳng tọa độ Oxy cho đường thẳng (d): y = 2(m - 1)x - m² + 3m và Parabol (P): y = x²

a) Với m = 3, tìm tọa độ giao điểm của (d) và (P)

b) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ là số đo chiều dài và chiều rộng của hình chữ nhật có diện tích bằng $\frac{7}{4}$ (đvdt).

Cho tam giác ABC vuông tại A. Đường tròn (O;R) đường kính AB cắt đoạn thẳng BC tại điểm thứ hai là D. Kẻ đường thẳng AH vuông góc với đường thẳng OC tại điểm H; đường thẳng AH cắt đoạn thẳng BC tại điểm M

1) Chứng minh tứ giác ACDH là tứ giác nội tiếp.

2) Chứng minh OH.OC = R và tam giác OHB đồng dạng với tam giác OBC

3) Từ O kẻ đường thẳng vuông góc với BD tại K. Chứng minh HM là tia phân giác của góc DHB và MB.MD = MK.MC

Cho a, b là các số thực không âm thỏa mãn a + b = 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=\sqrt{a\left(b+1\right)}+\sqrt{b\left(a+1\right)}.$

Câu lạc bộ Yêu thích học Toán của lớp có 2 học sinh nam và 3 học sinh nữ. Lớp trưởng chọn ngẫu nhiên 2 học sinh của câu lạc bộ để tham gia giao lưu chia sẻ kinh nghiệm. Tính xác suất để cả 2 học sinh được chọn đều là học sinh nữ.

Tính gần đúng thể tích của một hộp sữa có dạng hình trụ, bán kính đáy gần bằng 3,8cm và chiều cao gần bằng 8 cm. Kết quả làm tròn đến hàng phần mười.

1) Giải phương trình \({x^2} - 6x + 8 = 0.\)

2) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x - 2y = 8}\\{2x + 5y = 9.}\end{array}} \right.\)

3) Vẽ đồ thị của hàm số hàm số \(y = 2{x^2}.\)

1) Lập bảng tần số tương đối của mẫu dữ liệu thống kê năm chữ cái \[b,\,\,n,\,\,o,\,\,t,\,\,v\] trong câu “Học hành vất vả kết quả ngọt bùi”.

2) Chứng minh phương trình \({x^2} + 7x + 5 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) và tính giá trị của biểu thức \(M = x_1^2 + x_2^2 - 6{x_1}{x_2}.\)

1) Một thửa đất có dạng hình chữ nhật, chiều dài hơn chiều rộng 19 m và diện tích bằng \(150\,\,\;{{\rm{m}}^2}.\) Người ta dự định xây bức tường bao quanh thửa đất, xây theo chu vi của thửa đất, trừ 5 m của phần cổng. Biết giá tất cả các chi phí xây bức tường được tính với mỗi mét theo chu vi là 2 triệu đồng. Tính số tiền dự định xây bức tường đó.

2) Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x  - 1}} - \frac{{\sqrt x }}{{\sqrt x  + 1}} - \frac{2}{{x - 1}}\) (với \(0 \le x \ne 1).\)

Rút gọn biểu thức \(P\) và tìm \(x\) để \(P\) nhận giá trị nguyên.

3) Tháp nghiêng ở thành phố Pisa, Italia nghiêng khoảng \(4^\circ \) so với phương thẳng đứng. Người ta gắn ở mặt ngoài của tháp hai thiết bị tại hai vị trí \(A,\,\,B\) và nối với nhau bởi dây truyền tín hiệu. Tính gần đúng độ dài nhỏ nhất của dây đó, biết \(HB\) gần bằng \(3,146\,\,\;{\rm{m,}}\) với \(H\) là hình chiếu vuông góc của \(A\) trên mặt đất (xem hình trên). Kết quả làm tròn đến hàng phần trăm.

Cho điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB,\,\,AC\) lần lượt tại \(B,C\) của \(\left( O \right).\)

1) Chứng minh tứ giác \(ABOC\) nội tiếp đường tròn.

2) Vẽ đường kính \(BD\) của \(\left( O \right),\) đường thẳng đi qua điểm \(O\) vuông góc với \(AD\) cắt đường thẳng \(BC\) tại điểm \(E.\) Chứng minh \(ED\) là tiếp tuyến của \(\left( O \right).\)