13 CÂU HỎI
Một quả bóng đá tiêu chuẩn thường được sử dụng tại các giải thi đấu có diện tích bề mặt là Coi quả bóng đá có dạng hình cầu, tính thể tích của quả bóng (làm tròn kết quả đến một chữ số thập phân và lấy
Note note
Căn bậc hai số học của 81 là
9.
\[ - 9.\]
\( \pm 9.\)
\[6\,\,561.\]
Trong mặt phẳng tọa độ \[Oxy,\] cho điểm \(C\left( {2\,;\,\,4} \right)\) thuộc đồ thị \(\left( P \right)\) của hàm số \(y = a{x^2},\) với \(a \ne 0.\) Điểm \(C'\) đối xứng với điểm \(C\) qua trục tung \[Oy.\] Khẳng định nào sau đây là đúng?
Điểm \(C'\left( {2\,;\, - 4} \right)\) và \(C' \notin \left( P \right)\).
Điểm \(C'\left( { - 2\,;\,4} \right)\) và \(C' \in \left( P \right)\).
Điểm \(C'\left( { - 2\,;\,4} \right)\) và \(C' \notin \left( P \right)\).
Điểm \(C'\left( {4\,;\, - 2} \right)\) và \(C' \in \left( P \right)\).
Trong các phương trình sau, phương trình bậc hai một ẩn là
\({x^2}\sqrt 2 + 3x - 2 = 0\).
\(2{x^2} + 3\sqrt x - 2 = 0\).
\({x^2} \cdot \sqrt 2 + \frac{3}{x} - 2 = 0\).
\({x^2} \cdot \sqrt 2 + 3x - \frac{2}{{{x^2}}} = 0\).
Cho \(a\) và \(b\) là hai số thực tuỳ ý sao cho \(a < b\). Khẳng định nào sau đây là đúng?
\( - 2025a + 1 < - 2025b + 2\).
\(2025a + 1 > 2025b + 2\).
\( - 2025a < - 2025b - 2\).
\(2025a + 1 < 2025b + 2\).
Cặp số \(\left( {x\,;\,\,y} \right)\) nào dưới đây là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - 2y = 6}\\{2x + 3y = 10,5}\end{array}} \right.\)?
\(\left( {\frac{3}{2}\,;\,3} \right)\).
\(\left( {3\,;\,\frac{3}{2}} \right)\).
\(\left( {3\,;\,\frac{2}{3}} \right)\).
\(\left( {\frac{2}{3}\,;\,3} \right)\).
Trong các khẳng định sau, khẳng định nào đúng?
Đường tròn có vô số tâm đối xứng và chỉ có một trục đối xứng.
Đường tròn chỉ có một tâm đối xứng và có vô số trục đối xứng.
Đường tròn chỉ có một tâm đối xứng và một trục đối xứng.
Đường tròn có vô số tâm đối xứng và vô số trục đối xứng.
Cho hình vuông \[MNPQ\] (Hình 1). Phép quay thuận chiều tâm \(O\) biến điểm \(M\) thành điểm \(Q\) thì các điểm \[N,\,\,P,\,\,Q\] tương ứng thành các điểm
![Cho hình vuông \[MNPQ\] (Hình 1). Phép quay thuận chiều tâm \(O\) biến điểm \(M\) thành điểm \(Q\) thì các điểm \[N,\,\,P,\,\,Q\] tương ứng thành các điểm A. \[P,{\rm{ }}N,\,\,M\]. B. \[M,{\rm{ }}N,{\rm{ }}P\]. C. \[M,{\rm{ }}N,{\rm{ }}P\]. D. \[P,{\rm{ }}M,{\rm{ }}N\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid1-1728612638.png)
\[P,{\rm{ }}N,\,\,M\].
\[M,{\rm{ }}N,{\rm{ }}P\].
\[M,{\rm{ }}N,{\rm{ }}P\].
\[P,{\rm{ }}M,{\rm{ }}N\].
Cho tam giác \[ABC\] vuông tại \[C.\] Biết \(BC = 110\;\,{\rm{m}}\,;\,\,\widehat {BAC} = 20^\circ .\) Độ dài cạnh \[AC\] là
(Đơn vị tính: \(m;\) Kết quả làm tròn đến hàng đơn vị).
326.
328.
330.
302.
Từ điểm \(M\) nằm ngoài đường tròn tâm \(O\), kẻ hai tiếp tuyến \[MA,{\rm{ }}MB\] \[\left( {A,\,\,B} \right.\] là các tiếp điểm). Nếu \(AM = 4\,\,{\rm{cm}}\,{\rm{;}}\,\,\widehat {AMB} = 60^\circ \) thì
\(BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ \).
\(BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ \).
\(BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ \).
\(BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ \).
Một doanh nghiệp sản xuất thùng bằng tôn có dạng hình trụ với hai đáy (Hình 2).
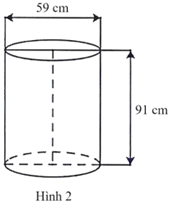Hình trụ đó có đường kính đáy khoảng \[59{\rm{ cm}}\] và chiều cao khoảng \[91{\rm{ cm}}.\] Chi phí để sản xuất thùng tôn đó là \[100\,\,000\] đồng \(/{{\rm{m}}^2}.\) Số tiền mà doanh nghiệp cần chi để sản xuất \[1\,\,000\] thùng tôn là
(Đơn vị tính: Đồng. Lấy \(\pi \approx 3,14,\) làm tròn kết quả đến hàng nghìn).
\[323\,\,238\,\,000.\]
\[223\,\,238\,\,000.\]
\[123\,\,238\,\,000.\]
Đáp án khác.
Bạn Lan gieo đồng thời hai đồng xu cân đối và đồng chất và quan sát mặt xuất hiện của đồng xu, thì không gian mẫu nhận được là
\[\left( {S,\,S} \right);\,\,\left( {S,\,N} \right);\,\,\left( {N,\,S} \right);\,\,\left( {N,\,N} \right)\].
\(\left( {S,S} \right);\,\,\left( {N,N} \right)\).
\(\left( {S,N} \right);\,\,\left( {N,S} \right)\).
\(\left( {S,\,S} \right);\,\,\left( {S,\,N} \right);\,\,\left( {N,\,S} \right)\).
Gieo một con xúc xắc 50 lần cho kết quả như bảng sau:
|
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
|
Tần số |
8 |
7 |
? |
8 |
6 |
11 |
Tần số tương đối xuất hiện của mặt 3 chấm là
\(20\% \).
\(10\% \).
\(8\% \).
\(6\% \).