16 câu hỏi
Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \[y = \frac{{{x^2} - 2x + m}}{{x - 1}}\] tiệm cận đứng. Khi đó tập hợp S bằng
R\{1}.
R\{0}.
R\{-1}.
R.
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, AC = 2a, BD = 3a, \[AC \bot BD\] và SA vuông góc với mặt phẳng (4BCD). Biết góc α giữa đường thẳng SC và mặt phẳng đáy thỏa mãn \[\cot \alpha = 3\]. Thể tích của khối chóp S.ABCD bằng
\[\frac{{{a^3}}}{{12}}.\]
\[\frac{{{a^3}}}{3}.\]
\[\frac{{{a^3}}}{4}.\]
\[\frac{{2{a^3}}}{3}.\]
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và SA = SC, SB = SD. Phát biểu nào sau đây là đúng?
\[SO \bot \left( {ABCD} \right)\]
\[AD \bot \left( {SAB} \right)\]
\[SA \bot AC\]
\[SA \bot BC\]
Tổng các nghiệm của phương trình \[{e^{{x^2}}} = {e^{3x - 2}}\] bằng
1.
2.
0.
3.
Bạn Minh định làm một vật thể có dạng hình trụ tròn xoay với bán kính đáy bằng 2 cm sao cho diện tích xung quanh của hình trụ bằng tổng diện tích hai mặt đáy của nó. Thể tích của khối trụ này bằng
4π cm3.
6π cm3.
8π cm3.
16π cm3.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1;3;4). Gọi A, B, C lần lượt là hình chiếu vuông góc của điểm M(-1;3;4) trên các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là
\[\frac{x}{{ - 1}} + \frac{y}{3} + \frac{z}{4} = 0.\]
\[\frac{x}{{ - 1}} + \frac{y}{3} - \frac{z}{4} = 0.\]
\[\frac{x}{1} + \frac{y}{3} - \frac{z}{4} = 1.\]
\[\frac{x}{1} - \frac{y}{3} - \frac{z}{4} = - 1.\]
Cho hàm số \[f\left( x \right) = x{e^{ - 2x}}\]. Tập nghiệm của phương trình \[f\left( x \right) = 0\] là
{1}.
\[\left\{ {\frac{1}{2}} \right\}\]
{0}.
\[\left\{ {\frac{{ - 1}}{2}} \right\}\]
Cho cấp số nhân (un) với u1 = 2025, công bội q. Đặt \[S = 4{u_2} + 5{u_3}\]. Để S đạt giá trị nhỏ nhất thì giá trị của q là
- 2025.
\[\frac{4}{5}\]
\[\frac{2}{5}\]
\[\frac{{ - 2}}{5}\]
Tập nghiệm của bất phương trình \[{\log _2}\left( {x - 1} \right) < - 1\] là
\[\left( {\frac{3}{2}; + \infty } \right).\]
\[\left( {1; + \infty } \right).\]
\[\left( {1;\frac{3}{2}} \right).\]
\[\left( { - \infty ;\frac{3}{2}} \right).\]
Cho đồ thị của hàm số y = f(x) như hình bên và diện tích hai phần tô đậm lần lượt là S1 = 10 và S2 = 3. Giá trị của \[\int_{ - 1}^2 {f\left( x \right)} dx\] bằng
![Cho đồ thị của hàm số y = f(x) như hình bên và diện tích hai phần tô đậm lần lượt là S1 = 10 và S2 = 3. Giá trị của \[\int_{ - 1}^2 {f\left( x \right)} dx\] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid0-1750473837.png)
7.
– 7.
5.
13.
Phương trình \[\sin \left( {x - \frac{\pi }{3}} \right) = 1\] có tập nghiệm là
\[\left\{ {\frac{{5\pi }}{6} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\]
\[\left\{ {\frac{{5\pi }}{6} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\]
\[\left\{ {\frac{\pi }{3} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\]
\[\left\{ {\frac{\pi }{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}.\]
Xét hai biến cố độc lập A, B thỏa mãn P(A) = 0,2 và P(B) = 0,3. Xác suất của biến cố \[A \cup \overline B \] bằng
0,14.
0,44.
0,76.
0,9.
Biểu đồ dưới đây thể hiện chi phí hoạt động của 4 công ty A, B, C, D cho ba hạng mục: Nhân sự, đầu tư và vận hành trong năm 2024 (đơn vị: tỉ đồng).
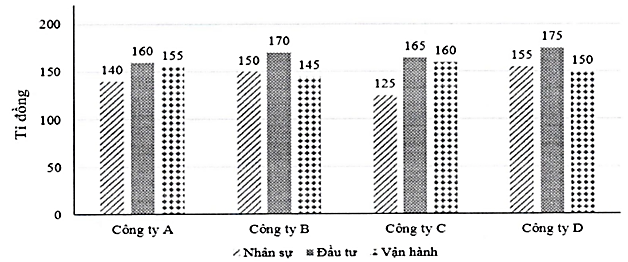
Chọn ngẫu nhiên một công ty trong các công ty đó. Xác suất để công ty được chọn ra có chi phí trung bình của ba hạng mục lớn hơn 154 tỉ đồng là
\[\frac{1}{4}\]
\[\frac{1}{2}\]
\[\frac{2}{3}\]
\[\frac{3}{4}\]
Cho hàm số y = f(x) có đạo hàm trên R và hàm số y = f'(x) có đồ thị như hình bên. Hàm số y = f(x) đồng biến trên khoảng nào sau đây?
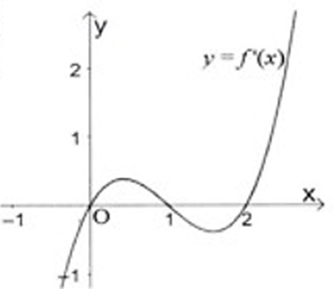
(1:2).
\[\left( { - \infty ;1} \right)\]
(0:1).
(-1;0).
Giá trị của m để hai mặt phẳng \[\left( \alpha \right):7x - 3y + mz - 5 = 0\] và \[\left( \beta \right):x - 3y + 4z + 1 = 0\] vuông góc với nhau là
- 1.
1.
- 4.
4.
Hàm số \[f\left( x \right) = 1 - \frac{1}{{{x^2}}}\] có một nguyên hàm là
\[{F_1}\left( x \right) = \frac{2}{{{x^3}}}.\]
\[{F_3}\left( x \right) = x + \frac{2}{{{x^3}}}.\]
\[{F_4}\left( x \right) = \frac{2}{x}.\]
\[{F_2}\left( x \right) = x + \frac{1}{x}.\]
