Đề thi định kì cuối học kì II Toán 4 (Đề số 8)
11 câu hỏi
Trong các phân số sau đây phân số lớn hơn 1 là
1/2
3/4
5/4
6/7
Trong các số: 105; 5643; 2718; 345 số nào chia hết cho 2
105
5643
2718
345
Trong hình bình hành ABCD có
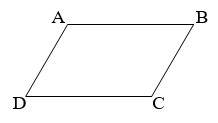
a) Cạnh AB bằng cạnh...
b) Cạnh AD bằng cạnh …..
c) Cạnh AB song song với cạnh...
d) Cạnh AD song song với cạnh....
Viết các số
a) Ba trăm sáu mươi lăm nghìn bảy trăm bốn mươi hai
b) Một trăm linh năm triệu không trăm bốn mươi ba nghìn không trăm linh chín
Chữ số 4 trong số 17 406 chỉ
4
40
400
4000
Số thích hợp để viết vào chỗ chấm để là
25
125
1025
125
Trung bình cộng của hai số bằng 30. Biết một trong hai số đó bằng 20, tìm số kia
Tính
Một hình bình hành có diện tích là 420. Biết chiều cao là 12cm. Tính độ dài đáy của hình bình hành đó
Tính bằng cách thuận tiện nhất
a) 5 x 36 x 2 b) 127 + 1 + 73 + 39
Một trường tiểu học có số học sinh gái ít hơn số học sinh trai là 120 học sinh. Hỏi trường đó có bao nhiêu học sinh trai, bao nhiêu học sinh gái, biết rằng số học sinh gái bằng 5/7 số học sinh trai








