Đề ôn luyện Toán theo Chủ đề 7. Thống kê (Đề số 2)
22 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Số đặc trưng nào không sử dụng thông tin giá trị của số liệu đầu tiên và giá trị của số liệu cuối cùng của mẫu số liệu không giảm?
Phương sai.
Độ lệch chuẩn.
Khoảng tứ phân vị.
Khoảng biến thiên.
Trung vị của dãy số 2; 3; 5; 6; 7 là
5.
6.
2.
4.
Kết quả thi môn Toán học kì 1 của lớp 10A trường THPT Triệu Sơn 1 được thống kê như sau:
Điểm thi | 5 | 6 | 7 | 8 | 9 | 10 |
Tần số | 5 | 7 | 8 | 12 | 8 | 5 |
Giá trị mốt \({M_0}\) của bảng phân bố tần số trên bằng
5.
12.
8.
7.
Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn Toán như sau: 5; 6; 7; 5; 8; 8; 10; 9; 7; 8. Tính điểm trung bình của tổ học sinh đó.
7.
8.
7,3.
7,5.
Cho mẫu số liệu sau
Giá trị | 2 | 3 | 4 | 5 | 6 |
Tần số | 4 | 2 | 5 | 2 | 6 |
Tìm độ lệch chuẩn của mẫu số liệu trên (kết quả làm tròn đến hàng phần trăm).
4,21.
2,28.
4,24.
1,51.
Cho mẫu số liệu ghép nhóm thời gian sử dụng internet trong 10 ngày (tính bằng đơn vị giờ) của 30 em học sinh lớp 12 trường THPT Quế Sơn như sau:
Số giờ | \(\left[ {5;10} \right)\) | \(\left[ {10;15} \right)\) | \(\left[ {15;20} \right)\) | \(\left[ {20;25} \right)\) | \(\left[ {25;30} \right)\) |
Số học sinh | 4 | 7 | 9 | 5 | 5 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng
30.
9.
20.
25.
Một mẫu số liệu có bảng tần số ghép nhóm như sau:
Nhóm | \(\left[ {1;5} \right)\) | \(\left[ {5;9} \right)\) | \(\left[ {9;13} \right)\) | \(\left[ {13;17} \right)\) | \(\left[ {17;21} \right)\) |
Tần số | 4 | 8 | 13 | 6 | 4 |
Phương sai của mẫu số liệu là
21,01.
20,01.
22.
23.
Một mẫu số liệu ghép nhóm có tứ phân vị là \({Q_1} = 54;{Q_2} = 61;{Q_3} = 73\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
19.
12.
7.
61.
Tất cả các bạn học sinh lớp 12A5 trả lời 32 câu hỏi trong một bài kiểm tra. Kết quả số câu trả lời đúng được thống kê ở bảng sau
Số câu trả lời đúng | \(\left[ {12;16} \right)\) | \(\left[ {16;20} \right)\) | \(\left[ {20;24} \right)\) | \(\left[ {24;28} \right)\) | \(\left[ {28;32} \right)\) |
Số học sinh | 4 | 8 | 8 | 16 | 4 |
Cỡ mẫu của mẫu số liệu ghép nhóm trên là
40.
20.
32.
30.
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Qua thống kê quãng đường 20 ngày đi bộ (đơn vị: km) của bác Hương tính được độ lệch chuẩn của mẫu số liệu ghép nhóm là 6. Phương sai của mẫu số liệu trên là
12.
2,45.
36.
13.
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết pin của một số máy vi tính cùng loại được mô tả bằng biểu đồ dưới đây.
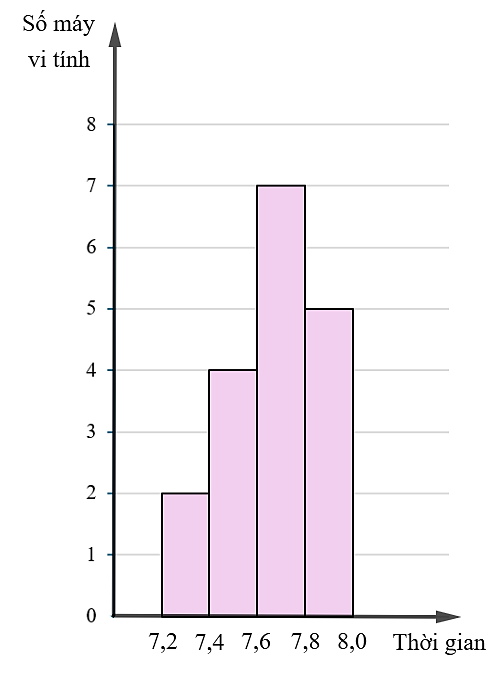
Hãy xác định số trung bình của thời gian sử dụng pin.
\(\frac{{37}}{5}\).
\(\frac{{25}}{3}\).
\(\frac{{23}}{3}\).
\(\frac{{73}}{{10}}\).
Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
Độ dài quãng đường (km) | \(\left[ {50;100} \right)\) | \(\left[ {100;150} \right)\) | \(\left[ {150;200} \right)\) | \(\left[ {200;250} \right)\) | \(\left[ {250;300} \right)\) |
Số ngày | 5 | 10 | 9 | 4 | 2 |
Độ lệch chuẩn của mẫu số liệu ghép nhóm (làm tròn đến hàng phần trăm).
55,68.
3000.
3100.
56,67.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Điểm thi của 35 học sinh trong kỳ thi Olympic cấp trường môn Toán lớp 10 (trên thang điểm 20) được thống kê bằng mẫu số liệu sau:
Điểm | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Số học sinh | 4 | 6 | 4 | 5 | 4 | 3 | 4 | 2 | 2 | 1 |
a) Số học sinh đạt điểm 10 (trên thang điểm 20) trong kỳ thi này là đông nhất.
b) Độ lệch chuẩn điểm của các học sinh trong bảng số liệu trên là \(s \approx 2,53\).
c) Trung vị của mẫu số liệu trên là 11 điểm.
d) Trong số các học sinh ở trên, có bạn Đăng Khôi lớp 10A cũng tham gia thi và đạt 14 điểm, đồng thời Khôi cũng thuộc nhóm 25% học sinh có số điểm cao nhất kỳ thi Olympic này.
Khảo sát số ghế trống tại một rạp chiếu phim trong 15 ngày, người ta thu được mẫu số liệu sau:
Số ghế trống | 7 | 8 | 12 | 13 | 15 |
|
Số ngày | 1 | 4 | 5 | 2 | 3 | \(n = 15\) |
a) Nếu thay đổi số ngày của mỗi số liệu số ghế trống đều bằng 3 thì khoảng biến thiên không thay đổi.
b) Có 25% giá trị của mẫu số liệu nằm giữa tứ phân vị thứ nhất và tứ phân vị thứ ba.
c) Số ngày có nhiều ghế trống nhất là 3 ngày.
d) Khảo sát thêm 2 ngày nữa thì thấy có 1 ngày có 6 ghế trống và 1 ngày có 16 ghế trống. Khi đó, trung vị của mẫu số liệu không thay đổi.
Thống kê thời gian (đơn vị: phút) tập thể dục buổi sáng mỗi ngày trong tháng 11 năm 2024 của An cho kết quả như sau:
Thời gian (phút) | \(\left[ {15;20} \right)\) | \(\left[ {20;25} \right)\) | \(\left[ {25;30} \right)\) | \(\left[ {30;35} \right)\) | \(\left[ {35;40} \right)\) |
Số ngày | 5 | 4 | 10 | 7 | 4 |
a) Nhóm chứa tứ phân vị thứ nhất là \(\left[ {25;30} \right)\).
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là 9,375.
c) Phương sai của mẫu số liệu là 36,14 (làm tròn kết quả đến hàng phần trăm).
d) Khoảng biến thiên của mẫu số liệu ghép nhóm là 25.
Hằng ngày ông Minh đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian ông Minh đi xe buýt từ nhà đến cơ quan.
Thời gian (phút) | \(\left[ {15;18} \right)\) | \(\left[ {18;21} \right)\) | \(\left[ {21;24} \right)\) | \(\left[ {24;27} \right)\) | \(\left[ {27;30} \right)\) | \(\left[ {30;33} \right)\) |
Số lần | 22 | 38 | 27 | 8 | 4 | 1 |
a) Tổng số lần ông Minh đã đi là 100.
b) Trong 100 lần ông Minh đã đi, hiệu số thời gian của hai lần bất kì không vượt quá 18 phút.
c) Khoảng tứ phân vị của mẫu số liệu là \({\Delta _Q} = 4,43\) (kết quả đã làm tròn đến hàng phần trăm).
d) Phương sai của mẫu số liệu đã cho bằng 10.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Thời gian anh Minh đi từ nhà đến công ty từ 20 đến 30 phút. Anh Minh đã thống kê thời gian đi làm của mình trong 1 tháng và thu được bảng tần số sau:
Thời gian (phút) | 20 | 22 | 24 | 25 | 27 | 28 | 30 |
Số lần | 1 | 4 | 11 | 8 | 3 | 1 | 2 |
Tính thời gian trung bình mà anh Minh đi từ nhà đến công ty trong tháng đó.
Mẫu số liệu sau đây cho biết số bài hát ở 10 album trong bộ sưu tập của An
12 | 7 | 10 | 9 | 12 | 9 | 10 | 11 | 10 | 14 |
Tìm khoảng tứ phân vị của mẫu số liệu đã cho.
Điều tra về độ tuổi của 200 cư dân trong một khu phố (đơn vị: độ tuổi) được kết quả cho trong bảng sau
Nhóm | \(\left[ {10;20} \right)\) | \(\left[ {20;30} \right)\) | \(\left[ {30;40} \right)\) | \(\left[ {40;50} \right)\) | \(\left[ {50;60} \right)\) | \(\left[ {60;70} \right)\) | \(\left[ {70;80} \right)\) | \(\left[ {80;90} \right)\) |
Tần số | 17 | 32 | 40 | 48 | 50 | 10 | 2 | 1 |
Tìm khoảng tứ phân vị của mẫu số liệu trên (kết quả làm tròn đến hàng phần chục).
Cự li cú nhảy 3 bước của 40 học sinh lớp 12 được ghi lại ở bảng tần số ghép nhóm sau:
Độ dài (m) | \(\left[ {9;10} \right)\) | \(\left[ {10;11} \right)\) | \(\left[ {11;12} \right)\) | \(\left[ {12;13} \right)\) | \(\left[ {13;14} \right)\) |
Tần số | 18 | 10 | 6 | 4 | 2 |
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần mười).
Cho bảng số liệu ghép nhóm về khoảng tuổi và số người như sau
Khoảng tuổi | \(\left[ {23;28} \right)\) | \(\left[ {28;33} \right)\) | \(\left[ {33;38} \right)\) | \(\left[ {38;43} \right)\) | \(\left[ {43;48} \right)\) |
Số người | 10 | 14 | 17 | 12 | 5 |
Khoảng biến thiên của mẫu số liệu là \(T = XY\). Tìm \(M = 2X + Y\).
Biểu đồ hình dưới đây thể hiện điểm trung bình môn Toán của 501 học sinh khối 12 một trường THPT. Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ này bằng bao nhiêu? (kết quả làm tròn đến hàng phần trăm).