Đề kiểm tra Vật Lí 11 Kết nối tri thức Chương 1 có đáp án - Đề 1
28 câu hỏi
PHẦN I. Câu trắc nhiệm nhiều phương án lựa chọn (4,5 điểm).
Thí sinh trả lời từ câu 1 đến câu 18. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong dao động điều hòa của một vật thì tập hợp ba đại lượng nào sau đây là không thay đổi theo thời gian
vận tốc, lực, năng lượng toàn phần.
biên độ, tần số, gia tốc.
biên độ, tần số, năng lượng toàn phần.
gia tốc, chu kỳ, lực.
Trong dao động điều hòa
khi gia tốc cực đại thì động năng cực tiểu.
khi cơ năng cực tiểu thì thế năng cực đại.
khi động năng cực đại thì thế năng cũng cực đại.
khi vận tốc cực đại thì pha dao động cũng cực đại.
Một vật dao động điều hoà với chu kỳ T, động năng của vật biến đổi theo thời gian
tuần hoàn với chu kỳ T.
tuần hoàn với chu kỳ 2T.
với một hàm sin hoặc cosin.
tuần hoàn với chu kỳ T/2.
Phát biểu nào sau đây về động năng và thế năng trong dao động điều hoà là sai?
Thế năng đạt giá trị cực tiểu khi độ lớn gia tốc của vật đạt giá trị cực tiểu.
Động năng đạt giá trị cực đại khi vật chuyển động qua vị trí cân bằng.
Thế năng đạt giá trị cực đại khi tốc độ của vật đạt giá trị cực đại.
Động năng đạt giá trị cực tiểu khi vật ở một trong hai vị trí biên.
Một vật có khối lượng m dao động điều hòa với biên độ A. Khi chu kì tăng 3 lần thì năng lượng của vật sẽ
tăng 3 lần.
giảm 9 lần.
tăng 9 lần.
giảm 3 lần.
Trong dao động điều hoà khi động năng giảm đi 2 lần so với động năng cực đại thì
thế năng đối với vị trí cân bằng tăng hai lần.
li độ dao động tăng 2 lần.
vận tốc dao động giảm \(\sqrt 2 \) lần.
gia tốc dao động tăng 2 lần.
Công thức tính chu kì dao động của con lắc lò xo là
T = 2π\(\sqrt {\frac{{\rm{k}}}{{\rm{m}}}} .\)
T = 2π\(\sqrt {\frac{{\rm{m}}}{{\rm{k}}}} .\)
T = 2\(\sqrt {\frac{{\pi {\rm{k}}}}{{\rm{m}}}} .\)
T = \(\frac{\pi }{2}\sqrt {\frac{{\rm{k}}}{{\rm{m}}}} .\)
Một con lắc đơn dao động điều hòa với tần số f. Nếu tăng khối lượng của con lắc lên 4 lần thì tần số dao động của nó sẽ là
2f.
\(\sqrt 2 f.\)
\(\frac{{\rm{f}}}{2}.\)
f.
Một vật dao động điều hòa, đồ thị biểu diễn mối quan hệ giữa thế năng Wt và động năng có dạng đường nào?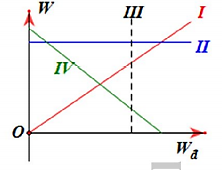
Đường IV.
Đường I.
Đường III.
Đường II.
Một con lắc đơn có độ dài dây ℓà 2m, treo quả nặng 1 kg, kéo con ℓắc ℓệch khỏi vị trí cân bằng góc 600 rồi buông tay. Thế năng cực đại của con ℓắc đơn bằng
1 J
5 J .
10 J .
15 J.
Một con lắc lò xo gồm lò xo có độ cứng 40 N/m gắn với quả cầu có khối lượng m. Cho quả cầu dao động với biên độ 5 cm. Động năng của quả cầu ở vị trí ứng li độ 3 cm bằng
0,032 J.
320 J.
0,018 J.
0,5 J.
Một con lắc lò xo gồm viên bi nhỏ và lò xo nhẹ có độ cứng100 N/m, dao động điều hòa với biên độ 0,1 m. Mốc thế năng ở vị trí cân bằng. Khi viên bi cách biên 6 cm thì động năng của con lắc bằng
0,64 J.
4,2 mJ.
6,4 mJ.
0,42 J.
Vật nhỏ của một con lắc lò xo có khối lượng100g dao động điều hòa với chu kì 0,2s, cơ năng là 0,18J (mốc thế năng tạivị trí cân bằng), lấy p2 =10. Tại li độ 3\[\sqrt[]{2}\] cm, tỉ số động năng và thế năng bằng
3.
4.
2
1.
Con lắc lò xo dao động với biên độ 6 cm. Li độ của vật để thế năng của lò xo bằng 1/3 động năng là
\( \pm 3\sqrt 2 cm\).
\( \pm 3cm\).
\( \pm 2\sqrt 2 cm\).
\( \pm \sqrt 2 cm\).
Một con lắc đơn có khối lượng m = 10 kg và chiều dài dây treo l = 2 m. Góc lệch cực đại so với đường thẳng đứng là \(\alpha = {10^0} = 0,175\;rad\). Lấy \(g = 10\;m/{s^2}\). Cơ năng của con lắc và vận tốc vật nặng khi nó ở vị trí thấp nhất là
W = 0,1525J; \({V_{max}}\) = 0,055 m/s.
W = 1,525J; \({V_{max}} = 0,55\) m/s.
W = 30,45J; \({V_{max}}\) = 7,8 m/s.
W = 3,063J; \({V_{max}} = 0,78\) m/s.
Một vật nhỏ có khối lượng 2/π2 g dao động điều hòa với tần số 5 Hz, và biên độ 5 cm. Cơ năng dao động bằng
2,5 J.
250 J.
0,25 J.
0,5 J.
Một con lắc lò xo dao động điều hòa với biên độ A = 10 cm. Đồ thị biểu diễn mối liên hệ giữa động năng và vận tốc của vật dao động được cho như hình vẽ. Chu kì và độ cứng của lò xo lần lượt là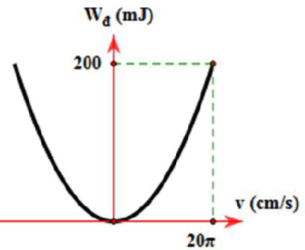
1 s và 4 N/m.
2π s và 40 N/m.
2π s và 4 N/m.
1 s và 40 N/m.
Một vật nhỏ dao động điều hòa dọc theo trục Ox. Khi vật cách vị trí cân bằng một đoạn 2 cm thì động năng của vật là 0,48 J. Khi vật cách vị trí cân bằng một đoạn 6 cm thì động năng của vật là 0,32 J. Biên độ dao động của vật bằng
8 cm.
14 cm.
10 cm.
12 cm.
Phần II. Câu trắc nghiệm đúng sai (4 điểm).
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Biết phương trình li độ của một vật có khối lượng 0,2 kg dao động điều hòa là: \(x = 5\cos (20t)cm.\)
| Phát biểu | Đúng | Sai |
a | Ta có: A = 0,05cm; ꞷ = 20 rad/s Cơ năng \(W = \,40J\) |
|
|
b | Biểu thức động năng và thế năng lần lượt là: ; \({W_t} = 0,1{\cos ^2}(20t)(J)\) |
|
|
c | Thế năng của con lắc tại thời điểm 2 giây là: \({W_t} = 17,79J\) |
|
|
d | Khi vật ở vị trí +A, ta có Wđmax = W: \({v_{max}} = 20\sqrt {10} \) cm/s |
|
|
Cho đồ thị vận tốc – thời gian của một con lắc đơn dao động như Hình 3.3. Biết rằng khối lượng của vật treo vào sợi dây là 0,2 kg.
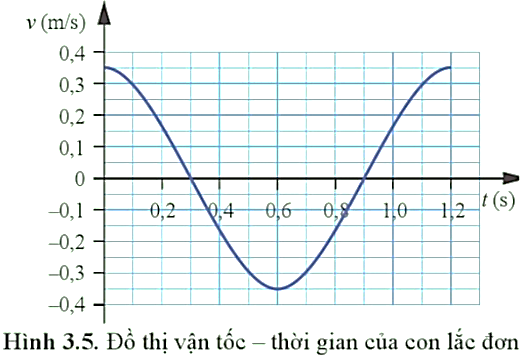
Hình 3.3. Đồ thị vận tốc – thời gian
| Phát biểu | Đúng | Sai |
a | Từ đồ thị ta có: \(\omega = \frac{{5\pi }}{3}(rad/s)\) |
|
|
b | Phương trình vận tốc: \(v = 0,35\cos \left( {\frac{{5\pi }}{3}t} \right)\left( {m/s} \right)\) |
|
|
c | Cơ năng của vật: W = \(4,{9.10^{ - 3}}J\) |
|
|
d | Tại thời điểm 0,4s thế năng của vật: \[{W_t} = 9,{1875.10^{ - 3}}J\] |
|
|
Một vật có khối lượng m = 1 kg, dao động điều hoà với chu kì T = 0,2π s, biên độ dao động bằng 2 cm.
| Phát biểu | Đúng | Sai |
a | Trong quá trình dao động, cơ năng của vật là được bảo toàn. |
|
|
b | Khi vật chuyển động từ vị trí cân bằng đến biên dương, thế năng tăng dần đều. |
|
|
c | Vận tốc cực đại của vật là vmax = 20 cm/s. |
|
|
d | Tại vị trí cân bằng, động năng của vật đạt cực đại: Wdmax = 200 mJ. |
|
|
Một con lắc đơn gồm vật nặng có khối lượng 1 kg, độ dài dây treo 2 m, góc lệch cực đại của dây so với đường thẳng đứng 0,175 rad. Chọn mốc thế năng trọng trường ngang với vị trí thấp nhất, \({\pi ^2} = 10\), g = 9,8m/s2.
| Phát biểu | Đúng | Sai |
a | Con lắc đơn dao động điều hòa với tần số góc \(\omega = \frac{{7\pi }}{{10}}\left( {rad/s} \right)\) |
|
|
b | Cơ năng của vật được bảo toàn nên ở vị trí thấp nhất W = 0,3 J |
|
|
c | Khi vật ở vị trí thấp nhất: Wđ = 0 |
|
|
d | Vận tốc của con lắc đơn khi qua vị trí thấp nhất theo chiều dương là: \({v_{max}} = \;0,77\;\;m/s\) |
|
|
PHẦN III. Câu trắc nghiệm trả lời ngắn
Một con lắc đơn có chiều dài \[l = 1,2\]m dao động nhỏ với tần số góc bằng 2,86 rad/s tại nơi có gia tốc trọng trường \[g\]. Giá trị của \[g\] tại đó bằng bao nhiêu m/s2 ? (Làm tròn đến chữ số thập phân thứ 2 sau dấu phẩy)
Một vật nhỏ có khối lượng bằng 100 g, dao động điều hòa với biên độ bằng 5 cm và chu kỳ bằng π s. Động năng cực đại của vật bằng bao nhiêu miliJun?
Một con lắc lò xo dao động điều hòa. Biết lò xo có độ cứng 36 N/m và vật nhỏ có khối lượng 100 g. Lấy π2 =10. Động năng của con lắc biến thiên theo thời gian với tần số ?
Một con lắc đơn có khối lượng 2 kg và có độ dài 4 m, dao động điều hòa ở nơi có gia tốc trọng trường 9,8 m/s2. Cơ năng dao động của con lắc là 0,2205 J. Biên độ góc (góc lệch lớn nhất) của con lắc bằng bao nhiêu độ? (Làm tròn đến 1 số thập phân)
Động năng dao động của một con lắc lò xo được mô tả theo thế năng dao động của nó bằng đồ thị như hình vẽ. Cho biết khối lượng của vật bằng 100 g, vật dao động giữa hai vị trí cách nhau 8cm. Tính tần số góc của dao động của con lắc lò xo. (Làm tròn đến 2 chữ số thập phân)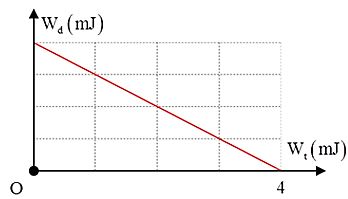
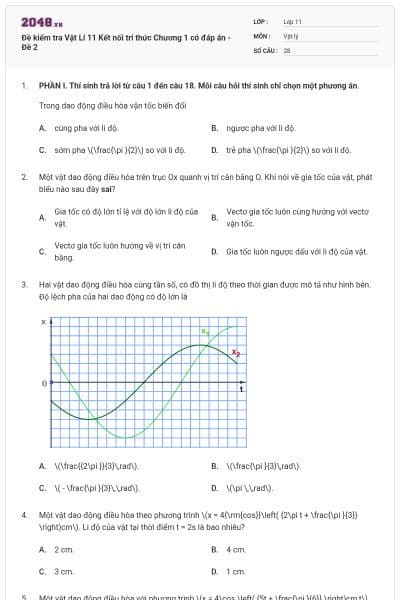
Hai con lắc lò xo dao động điều hòa có động năng biến thiên theo thời gian như đồ thị, con lắc (1) là đường liền nét và con lắc (2) là đường nét đứt. Vào thời điểm thế năng 2 con lắc bằng nhau thì tỉ số động năng con lắc (1) và động năng con lắc (2) là bao nhiêu ?