Đề kiểm tra Toán 9 Chân trời sáng tạo Chương 4 có đáp án - Đề 2
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho \[\alpha ,\,\,\beta \] là hai góc phụ nhau. Kết luận nào sau đây đúng?
\[\sin \alpha = \cot \beta .\]
\[\sin \alpha = \tan \beta .\]
\[\sin \alpha = \cos \beta .\]
\[{\rm{cos}}\alpha = \cot \beta .\]
Hình bên mô tả một chiếc thang có chiều dài \[AB = 4\,\,{\mathop{\rm m}\nolimits} \]được đặt dựa vào tường, khoảng cách từ chân thang đến chân tường là \[BH = 1,5\,\,{\mathop{\rm m}\nolimits} .\] Số đo góc tạo bởi cạnh \[AB\] và phần tường nằm ngang trên mặt đất là![Chọn D Ta có, góc tạo bởi cạnh \[AB\] và phương năm ngang trên mặt đất là \[\widehat {ABH}\]. Xét tam giác \[ABH\] vuôn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/8-1761181578.png)
\(\widehat {ABH} \approx 67^\circ .\)
\(\widehat {ABH} \approx 69^\circ .\)
\(\widehat {ABH} \approx 66^\circ .\)
\(\widehat {ABH} \approx 68^\circ .\)
Cho tam giác \[DEF\] vuông tại \[D\] có \[DE = \sqrt 2 {\rm{\;cm}},\,\,EF = \sqrt {10} {\rm{\;cm}}.\] Tỉ số lượng giác \[\cot E\] là
\[\cot E = \frac{1}{2}.\]
\[\cot E = 2.\]
\[\cot E = \frac{{\sqrt 5 }}{5}.\]
\[\cot E = \sqrt 5 .\]
Một khúc sông rộng khoảng \[130\,\,{\rm{m}}\]. Một con đò dự định chèo từ bờ bên này sang bờ bên kia theo phương vuông góc với bờ sông, nhưng do bị dòng nước đẩy xiên nên phải chèo khoảng \[150\,\,{\rm{m}}\]mới sang được bờ bên kia. Dòng nước đã đẩy con đò lệch đi một góc so với phương dự định ban đầu là
\[{\rm{30}}^\circ \].
\[29^\circ \].
\[{\rm{41}}^\circ \].
\[6{\rm{0}}^\circ \].
Trên một cái thang dài \[3,5\,\,{\rm{m}}\] người ta ghi: “Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ \[6{\rm{0}}^\circ \] đến \[7{\rm{0}}^\circ \]”. Gọi \[x\,\,({\rm{m}})\] (với \[x > 0\]) là khoảng cách từ chân thang đến chân tường để đảm bảo an toàn khi sử dụng chiếc thang này, tìm điều kiện của \[x\]. Trong các kết quả sau, kết quả nào đúng? (làm tròn kết quả đến hai chữ số phần thập phân).
\[1,20\, < x < 1,75\].
\[1,20\, \le x \le 1,75\].
\[x = 1,20\] hoặc \[x = 1,75\].
\[1,20 \le x < 1,75\].
Cho hình thang \[ABCD\] có \[\widehat {A\,} = \widehat {D\,} = 90^\circ ,\,\,\widehat {C\,} = 50^\circ .\] Biết rằng \[AB = 2;\,\,AD = 1,2.\] Khi đó diện tích hình thang \[ABCD\]gần nhất với
\[5\] (đvdt).
\[4\](đvdt).
\[3\](đvdt).
\[2\](đvdt).
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác \(ABC\) có \(\widehat A = 15^\circ \,;\,\,\widehat B = 30^\circ \,;\,\,AB = 15\,\,{\rm{cm}}{\rm{.}}\) Kẻ \(AH \bot BC\) tại \(H.\)
a) Tam giác \(ABC\) là tam giác nhọn.
b) Độ dài \(AH\) là \(7,5\,\,{\rm{cm}}\).
c) Tam giác \(HAC\) là tam giác nhọn.
d) Diện tích tam giác \(ABC\) khoảng \(20\,\,{\rm{c}}{{\rm{m}}^2}\) (khi làm tròn đến hàng đơn vị).
Để lắp đường điện cao thế từ vị trí \[A\] đến vị trí \[B\] cách nhau \[2\,\,000{\rm{ m}},\] do phải tránh ngọn núi nên người ta nối đường dây từ vị trí \[A\] đến vị trí \[C,\] rồi nối từ vị trí \[C\] đến vị trí \[B.\] Góc tạo bởi hai đoạn dây \[CA\] và \[CB\] là \(90^\circ \) và góc tạo bởi đoạn dây \[AC\] và đường \[AB\] là \(60^\circ \).
![a) Độ dài \[AC\] đường dây (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/45-1761183430.png)
a) Độ dài \[AC\] đường dây điện nối từ \[A\] đến \[C\] là \(1\,\,000\;\,{\rm{m}}{\rm{.}}\)
b) Độ dài \[AB\] đường dây điện nối từ \[A\] đến \[B\] là \(1\,\,624\;\,{\rm{m}}{\rm{.}}\)
c) Tổng độ dài đường dây điện nối từ \[A\] đến \[C\] rồi nối tiếp đến \[B\] là \(2\,\,732\,\;\,{\rm{m}}{\rm{.}}\)
d) Chiều dài tăng thêm của đường dây điện là \(735\;{\rm{m}}\).
Phần 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tháp Eiffel là một công trình kiến trúc bằng thép nằm trên công viên Champ-de-Mars, cạnh sông Seinc, là biểu tượng của Thủ đô Paris nước Pháp. Công trình này do kỹ sư Gustave Eiffel và các đồng nghiệp của mình thiết kế, xây dựng từ năm 1887 đến năm 1889 nhân dịp Triển lãm thế giới năm 1889 và cũng là dịp kỷ niệm 100 năm Cách mạng Pháp.Hãy tính chiều cao của tháp Eiffel mà không cần lên đỉnh tháp, biết góc tạo bởi tia nắng mặt trời với mặt đất là \(62^\circ {\rm{C}}\) và bóng của tháp trên mặt đất là \[175{\rm{ m}}\] (đơn vị mét, làm tròn kết quả đến hàng đơn vị).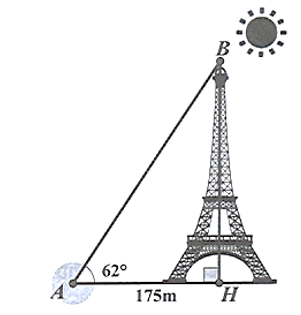
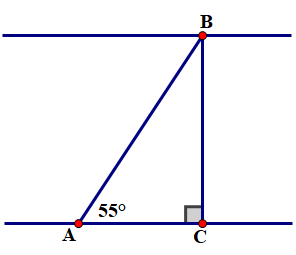
Một cano chạy với tốc độ \(10\;\,{\rm{km}}/{\rm{h}}\) vượt qua một khúc sông nước chảy mạnh mất 6 phút. Biết rằng đường đi của ca nô tạo với bờ một góc \(55^\circ .\) Tính chiều rộng \[BC\] của khúc sông (đơn vị mét, làm tròn đến hàng đơn vị).
Để xác định chiều cao \[AH\] của một ngọn núi, người quan sát đứng từ hai vị trí \[B\] và \[C\] cách nhau \[475\,\,{\rm{m}}\] trên mặt đất. Tại vị trí \[B\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng \[34^\circ \]; tại vị trí \[C\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng \[30^\circ \] (hình vẽ). Biết rằng tầm mắt của người quan sát là \[{\rm{1,6}}\,\,{\rm{m}}\] và giả thiết ba điểm \[H,\,\,B,\,\,C\] thẳng hàng. Tính chiều cao của ngọn núi (đơn vị mét, kết quả làm tròn đến hàng đơn vị).
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)


