Đề kiểm tra Toán 9 Chân trời sáng tạo Chương 3 có đáp án - Đề 1
11 câu hỏi
Căn bậc hai của 9 là
3.
\(\sqrt 3 \).
3 và \[ - 3.\]
\[ - 3.\]
Khẳng định nào dưới đây là đúng?
Số âm không có căn bậc 3.
\[\sqrt {0,48} > 0,7\].
\[\left( {2 - \sqrt[3]{3}} \right)\left( {2 + \sqrt[3]{3}} \right) = - 1.\]
\[\sqrt {\frac{4}{3}} > \sqrt {\frac{3}{4}} .\]
Cho \(M = 5\) và \(N = \frac{{\sqrt {50} }}{2}\). Khẳng định nào sau đây là đúng?
\(M < N\).
\(M + 2 = N\).
\(M = N\).
\(M > N\).
Kết quả thu gọn của biểu thức \[\left( {\sqrt[3]{3} + 1} \right)\left( {\sqrt[3]{9} + \sqrt[3]{3} + 1} \right)\] là
\[\sqrt[3]{3}\].
1.
9.
4.
Một cái thang dựa vào tường như hình bên dưới. Biết thang dài \[2\,\,{\mathop{\rm m}\nolimits} \] và tường cao \[1,3\,\,{\rm{m}}.\] Khoảng cách từ chân thang tới góc tường là
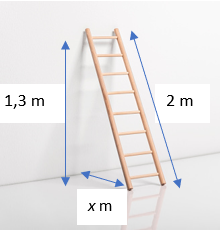
\[2,13{\rm{ m}}{\rm{.}}\]
\[1,98{\rm{ m}}.\]
\[1,5{\rm{ m}}.\]
\[1,3{\rm{ m}}.\]
Cho biểu thức \(P = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \frac{1}{{\sqrt x - 1}}} \right):\left( {1 - \frac{{x + 4}}{{x + \sqrt x + 1}}} \right)\). Các giá trị nguyên của \(x\) để \(P\) nhận giá trị nguyên dương là
\(x = 1\,;\,\;x = 36\).
\(x = - 1\,;\,\;x = 36.\)
\(x = 4\,;\,\;x = 6\). ).
\(x = 16\,;\,\;x = 36\
Cho biểu thức \[A = \sqrt {\sqrt {17} - 1} \cdot \sqrt {\sqrt {17} + 1} \] và biểu thức \[B = \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} + \sqrt {{{\left( {\sqrt 5 - 5} \right)}^2}} .\]
a) Kết quả thực hiện phép tính biểu thức \[A\] là \[16\].
b) Kết quả thực hiện phép tính biểu thức \[B\] là \[3.\]
c) So sánh giá trị biểu thức \[A\] và biểu thức \[B\] ta được \[A > B.\]
d) Kết quả phép tính \[A - 2B\] là \[2.\]
Cho biểu thức \(M = \sqrt {x - 1} + \frac{1}{{x - 3}} + \sqrt[3]{{x - 2}}\).
a) Điều kiện xác định của \(\sqrt[3]{{x - 2}}\) là \(x \ge 2.\)
b) Điều kiện của \(x\) để biểu thức \(M\) có nghĩa là \(x \ge 2.\)
c) Khi \(x = 1\) thì giá trị của biểu thức \(M\) là \[\frac{{ - 3}}{2}.\]
d) Khi \(\sqrt[3]{{x - 2}} = 0\) thì giá trị của biểu thức \(M\) là \(0\).
Công thức \(h = 0,4\sqrt[3]{x}\) biểu diễn mối tương quan giữa cân nặng \[x\] (tính bằng kg) và chiều cao \[h\] (tính bằng m) của một con hươu cao cổ. Một con hươu cao cổ cân nặng \[180{\rm{ kg}}\] thì cao bao nhiêu mét? (làm tròn đến chữ số thập phân thứ hai)
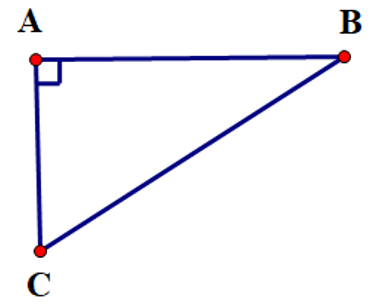
Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí \(A\) đến trường. Trường của anh An ở vị trí \(B\) và trường của em Bình ở vị trí \(C\) theo hai hướng vuông góc với nhau (như hình vẽ). Anh An đi với tốc độ \(4\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 15 phút. Em Bình đi với tốc độ \(3\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 12 phút. Tính khoảng cách \(BC\) giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).
Tốc độ chuyển động \(v\,\,({\rm{m}}\,{\rm{/}}\,{\rm{s}})\) của một vệ tinh nhân tạo quay quanh Trái Đất theo quỹ đạo tròn được tính bởi công thức:
\(v = R\sqrt {\frac{g}{{R + h}}} \).
Trong đó \[g \approx 9,81\;\,{\rm{m}}\,{\rm{/}}\,{{\rm{s}}^{\rm{2}}}\] là gia tốc trọng trường;
\(R = 6,378 \cdot {10^6}{\rm{\;m}}\) là bán kính Trái Đất,
\(h\,\,({\rm{m)}}\) là độ cao của vệ tinh so với mặt đất.
Hỏi ở độ cao so với mặt đất \[200{\rm{ km}}\] thì tốc độ của vệ tinh là bao nhiêu \({\rm{m}}/{\rm{s}}\)? (làm tròn đến hàng chục)


