Đề kiểm tra Toán 9 Cánh diều Chương 4 có đáp án - Đề 2
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho \[\alpha ,\,\,\beta \] là hai góc phụ nhau. Kết luận nào sau đây đúng?
\[\sin \alpha = \cot \beta .\]
\[\sin \alpha = \tan \beta .\]
\[\sin \alpha = \cos \beta .\]
\[{\rm{cos}}\alpha = \cot \beta .\]
Một chiếc thang có chiều dài từ chân lên đến nấc thang cuối là \[5\,\,{\rm{m}}\] được đặt vào thân cây cau như hình vẽ dưới đây, người ta đo được khoảng cách từ chân thang đến gốc cây cau là \[2,5\,\,{\rm{m}}{\rm{.}}\] Hỏi số đo góc \[\alpha \] tạo bởi thang và thân cây cau là bao nhiêu? (làm tròn kết quả đến độ).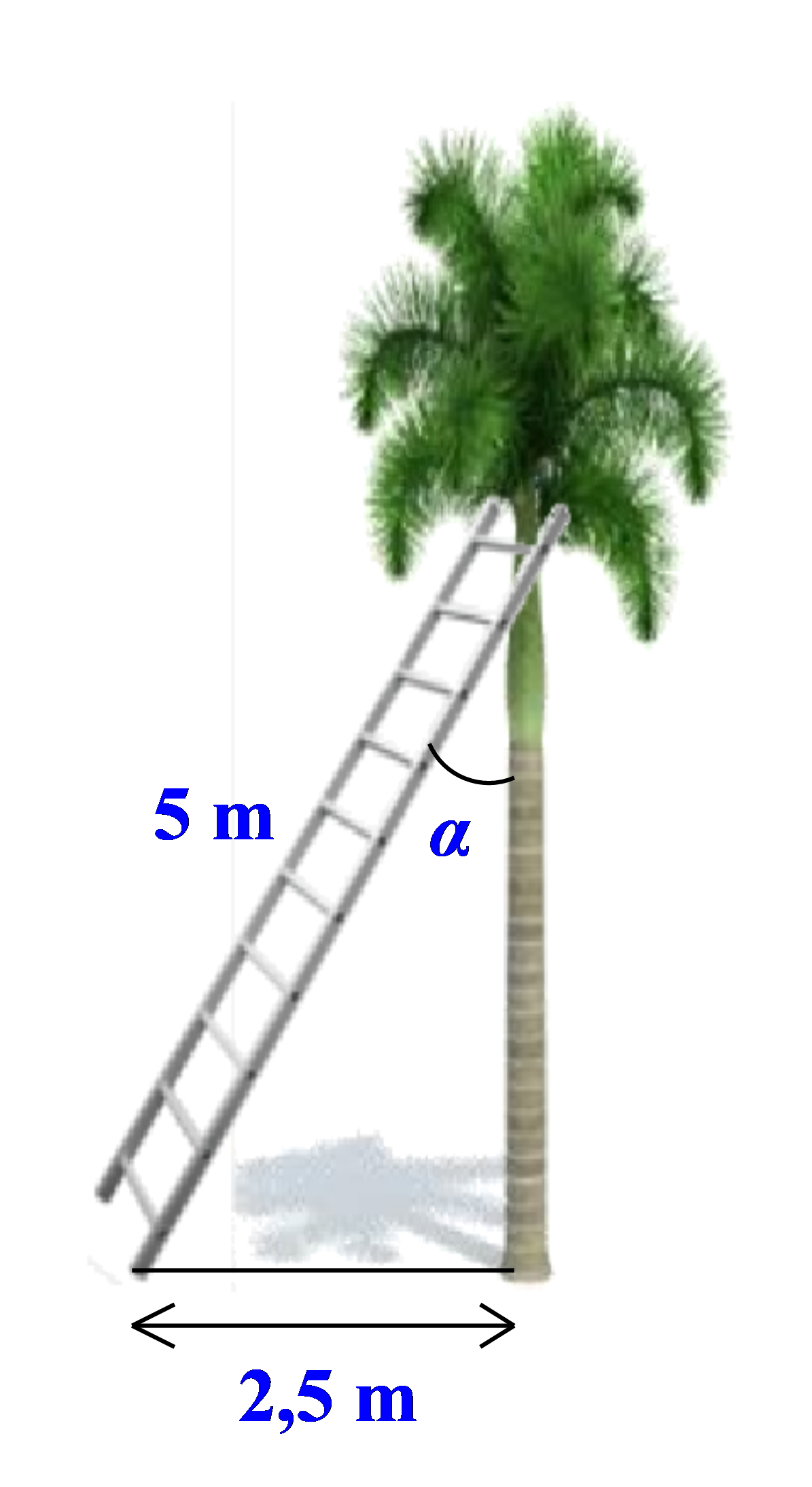
\[\alpha = 60^\circ \].
\[\alpha = 45^\circ \].
\[\alpha = 40^\circ \].
\[\alpha = 30^\circ \].
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,\,{\rm{cm}}\,;\,\,\widehat C = 30^\circ \). Độ dài các cạnh\(AB,\,\,BC\) lần lượt là
\[AB = \frac{{5\sqrt 3 }}{3}\,\,{\rm{cm}}\,;\,\,BC = \frac{{20\sqrt 3 }}{3}\,\,{\rm{cm}}\].
\(AB = \frac{{10\sqrt 3 }}{3};\,\,BC = \frac{{14\sqrt 3 }}{3}\).
\[AB = \frac{{10\sqrt 3 }}{3}\,\,{\rm{cm}}\,;\,\,BC = 20\sqrt 3 \,\,{\rm{cm}}\].
\(AB = \frac{{10\sqrt 3 }}{3}\,\,{\rm{cm}};\,\,BC = \frac{{20\sqrt 3 }}{3}\,\,{\rm{cm}}\).
Trong bóng đá, đá phạt đền là một hình thức đá phạt trực tiếp giữa 1 cầu thủ và 1 thủ môn. Bóng sẽ được đặt ở vị trí nằm trên đường trung trực của khung thành và cách khung thành \[11{\rm{ m}}.\] Biết chiều dài khung thành là \(7,23\,\;{\rm{m}}\). Góc sút \(\widehat {BAC}\)của cầu thủ khoảng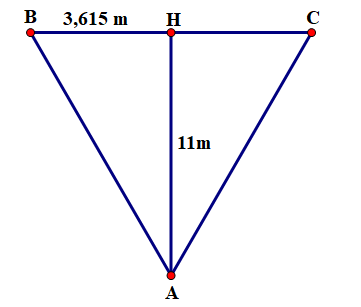
\(48^\circ .\)
\(36^\circ \).
\(24^\circ .\)
\(45^\circ .\)
Cho tam giác \(ABC\) có \(BC = 9\,\,{\rm{cm}}\,;\,\,\widehat {ABC} = 50^\circ \) và \[\widehat {ACB} = 35^\circ \]. Gọi \(N\) là chân đường vuông góc hạ từ \(A\) xuống cạnh\(BC\). Độ dài \(AN\) gần nhất với giá trị nào dưới đây?
\(5\,\,{\rm{cm}}{\rm{.}}\)
\(4\,\,{\rm{cm}}\).
\(2\,\,{\rm{cm}}\).
\(3\,\,{\rm{cm}}\).
Để đo chiều cao của một bức tường Điệp dùng một quyển sách và ngắm sao cho hai cạnh bia của quyển sách hướng về vị trí cao nhất và vị trí thấp nhất của bức tường (tham khảo hình vẽ). Biết rằng Điệp đứng cách tường \(1,5\;\,{\rm{m}}\) và vị trí mắt khi quan sát cách mặt đất là \(1,2\;\,{\rm{m}}\).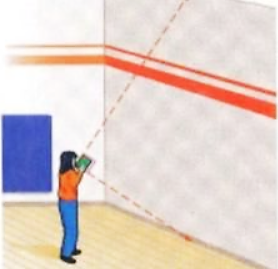
Hỏi chiều cao của bức tường là bao nhiêu? (kết quả làm tròn đến hàng đơn vị).
\[2{\rm{ m}}.\]
\[8{\rm{ m}}.\]
\[3{\rm{ m}}.\]
\[8{\rm{ m}}.\]
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (như hình bên dưới), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1225\,\,{\rm{m}}\] và dùng giác kế ngắm xác định được \[\widehat {ABC} = {75^{\rm{o}}}\]; \[\widehat {ACB} = {65^{\rm{o}}}\]. Tính khoảng cách \[AC\] (kết quả làm tròn đến đơn vị mét).
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/43-1761183381.png)
a) \[\widehat {BAC} = 40^\circ {\rm{.}}\]
b) Tam giác \[ABC\] nhọn.
c) \[\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\].
d) Khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát là \[1625{\rm{ m}}{\rm{.}}\]
Cho tam giác \(ABC\) nhọn, hai đường cao \(AD,\,\,BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\).
a) \(BD = AD \cdot \tan B\).
b) \(AD = CD \cdot \tan C\).
c) \(BD \cdot CD = DH \cdot AD\).
d) \(\tan B \cdot \tan C = 3\).
Phần 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tòa nhà Landmart 81 là một tòa nhà cao tầng ngay bên bờ sông Sài Gòn tại TP. Hồ Chí Minh. Tòa nhà này có 81 tầng, cao nhất Đông Nam Á (năm 2018). Ý tưởng thiết kế của The Landmark 81 được lấy cảm hứng từ những bó tre truyền thống tượng trưng cho sức mạnh và sự đoàn kết trong văn hóa Việt Nam. Tại một thời điểm tia sáng mặt trời tạo với mặt đất một góc là \(63^\circ \) (góc B) thì người ta đo được bóng của tòa nhà trên mặt đất dài khoảng \[235{\rm{ m}}\] (độ dài \[AB).\] Hãy ước tính chiều cao của tòa nhà này (đoạn thẳng \[AH\]) (làm tròn kết quả đến chữ số thập phân thứ nhất).
![Lời giải Xét \(\Delta ABH\) vuông tại \(A\), ta có: \(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\). Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\] Đáp án: 461. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/67-1761202758.png)
Một chiếc cầu trượt bao gồm phần cầu thang (để bước lên) và phần ống trượt (để trượt xuống) nối liền nhau như hình vẽ. Biết rằng khi xây dựng, phần ống trượt nghiêng với mặt đất một góc là \(35^\circ ,\) phần cầu thang (xem như đoạn thẳng \[AB)\] nghiêng với mặt đất một góc \(45^\circ ,\) khoảng cách từ chân thang đến chân ống trượt là \(3,58\;\,{\rm{m}}{\rm{.}}\) Tính độ cao \[AH\] của cầu trượt. (làm tròn đến chữ số thập phân thứ hai)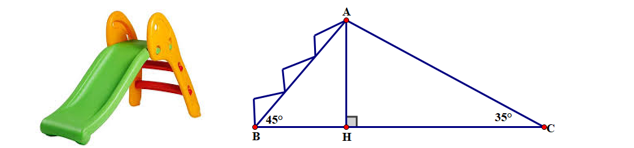
Mỗi ngày đi học, bạn Hùng phải đi đò (điểm \(A\)) qua một khúc sông rộng \[217{\rm{ m}}\] đến điểm \[B\] (bờ bên kia), rồi từ \[B\] đi bộ đến trường tại điểm \(D\) với quãng đường \(BD = 170\,\;{\rm{m}}\) (hình vẽ). Thực tế, do nước chảy, nên chiếc đò bị dòng nước đẩy xiên một góc \(50^\circ \) đưa bạn tới điểm \[C\] (bờ bên kia). Từ \[C\] bạn Hùng đi bộ đến trường. Tính quãng đường mà Hùng đã đi từ \(A\) đến \(D\) (kết quả làm tròn đến hàng đơn vị).