Đề kiểm tra Toán 12 Kết nối tri thức Chương 1 có đáp án - Đề 1
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
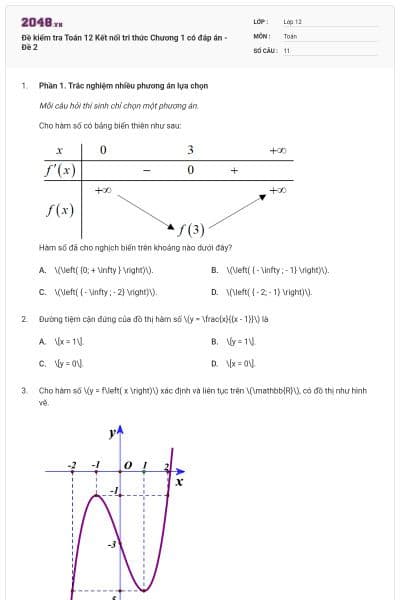
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1;0} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\).
Phương trình đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 5}}{{x + 1}}\) là:
\(y = 2\).
\(y = 3\).
\(y = - 1\).
\(x = 1\).
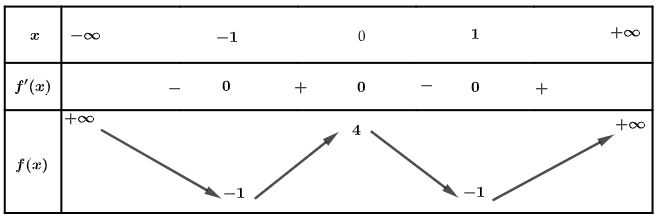
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định sai?
Hàm số có giá trị cực tiểu bằng \( - 1\).
Hàm số có giá trị nhỏ nhất bằng \( - 1\).
Hàm số có đúng một cực trị.
Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1\).
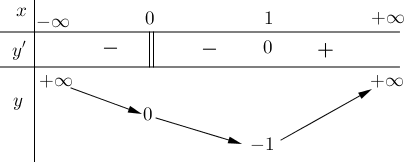
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau:
Số nghiệm phương trình \(2f\left( x \right) - 5 = 0\) là:
\(2\).
\(1\).
\(3\).
\(0\).
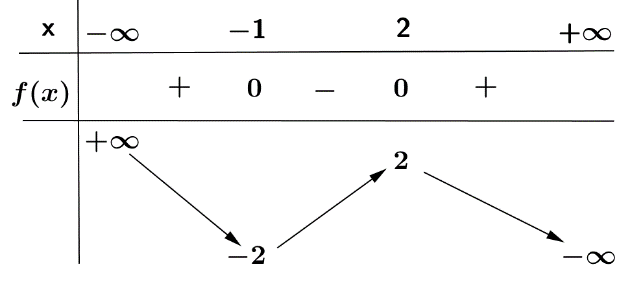
Đường cong dưới là đồ thị của hàm số nào trong các đáp án A, B, C, D?
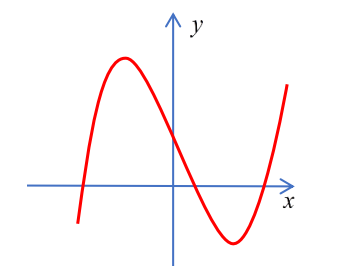
\(y = - {x^3} + 12x + 2\).
\(y = - {x^4} + 2{x^2} + 1\).
\(y = {x^3} - 3x - 2\).
\(y = {x^3} - 12x + 2\).
Hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left( { - \infty ; + \infty } \right)\) có bảng biến thiên như hình vẽ sau.
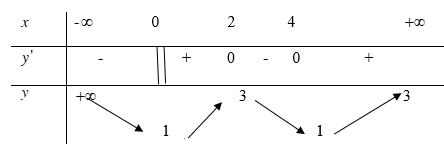
Giá trị lớn nhất của \(y = f\left( x \right)\) trên \(\left[ {1;5} \right]\) bằng
\(2\).
\(4\).
\(3\).
\(1\).
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y = f'\left( x \right)\)là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.
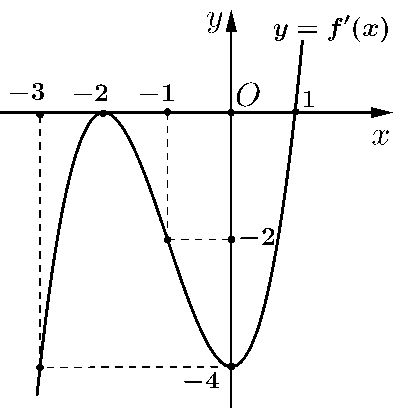
a) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
b) Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
c) \(f'\left( 2 \right) = 4\).
d) Hàm số \(g\left( x \right) = f\left( x \right) - \frac{1}{2}{x^2} + x + 2024\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao \[250\]km so với bề mặt của Mặt Trăng. Trong khoảng \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao \(h\) của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm \(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\) trong đó \(t\) là thời gian tính bằng giây và \(h\) là độ cao tính bằng kilomet.
a) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao lớn nhất mà con tàu đạt được là \(250\)(km).
b) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao thấp nhất mà con tàu đạt được tại thời điểm \(t \approx 25\)(s).
c) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, vận tốc của con tàu lớn nhất mà con tàu đạt được là \(10,33\,\)(km/s).
d) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao con tàu đạt được khi vận tốc của con tàu lớn nhất là \(139,37\,\)(km).
Phần 3. Trắc nghiệm trả lời ngắn
Một chất điểm chuyển động theo quy luật \(S\left( t \right) = 6{t^2} - {t^3}\). Vận tốc \(v\)(m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm \(t\)(s) bằng bao nhiêu giây?
Ông Nam cần xây dựng một bể nước mưa có thể tích \(V = 8\left( {{m^3}} \right)\) dạng hình hộp chữ nhật với chiều dài gấp \(\frac{4}{3}\) lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980.000đ/m2 và ở nắp để hở một khoảng hình vuông có diện tích bằng \(\frac{2}{9}\) diện tích nắp bể. Tính chi phí thấp nhất mà ông Nam phải chi trả (làm tròn đến hàng triệu đồng).
Một con cá hồi bơi ngược dòng (từ nơi sinh sống) vượt khoảng cách \[300km\]để tới nơi sinh sản. Vận tốc dòng nước là \[6km/h\]. Giả sử vận tốc bơi của cá khi nước đứng yên là \[v{\rm{ }}km/h\] thì năng lượng tiêu hao của cả trong \(t\) giờ cho bởi công thức \(E\left( v \right) = c{v^3}t\) trong đó \(c\) là hàng số cho trước. \(E\) tính hằng Jun. Tình vận tốc bơi của cả khi nước đứng yên, để năng lượng của cả tiêu hao ít nhất?