Đề kiểm tra Toán 12 Chân trời sáng tạo Chương 4 có đáp án - Đề 2
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trên khoảng \(\left( { - \infty ; + \infty } \right)\), hàm số \[F\left( x \right) = \frac{1}{2}\sin 2x\] là một nguyên hàm của hàm số nào dưới đây?
\({f_3}\left( x \right) = - \frac{1}{2}\cos 2x\).
\({f_4}\left( x \right) = - \frac{1}{4}\cos 2x\).
\({f_2}\left( x \right) = \cos 2x\).
\({f_1}\left( x \right) = - \cos 2x\).
Cho hàm số\[f\left( x \right) = {e^x} + 2x\]. Khẳng định nào dưới đây đúng?
\[\int {f\left( x \right)} = {e^x} + 2x + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} + 2{x^2} + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} - {x^2} + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} + {x^2} + C\].
Cho \[\int\limits_1^2 {f(x){\rm{d}}x = 3} \], \[\int\limits_1^2 {g(x){\rm{d}}x = 2} \]. Giá trị \[\int\limits_1^2 {\left[ {f(x) + g(x)} \right]{\rm{d}}x} \] bằng
\( - 1\).
\(6\).
\(1\).
\(5\).
Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là \(x(0 \le x \le 3)\) ta được mặt cắt là một hình vuông có cạnh là \(\sqrt {9 - {x^2}} \) (được mô hình hóa bởi hình vẽ bên dưới).![Chọn C Diện tích hình vuông có cạnh là \(\sqrt {9 - {x^2}} \) là \[S = 9 - {x^2}\]. Thể tích của vật thể đó bằng \[\int\limits_0^3 {\left( {9 - {x^2}} \right)} \,{\rm{d}}x = \left. {\left( {9x - \frac{{{x^3}}}{3}} \right)} \right|_0^3 = 18\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/1-1759411506.png)
Thể tích của vật thể đó bằng
\(171\pi \).
\(18\pi \).
\(18\).
\(171\)
Hàm số \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right) = 3{x^2}\) và \(F\left( 0 \right) = 5\). Khi đó, hàm số \(F\left( x \right)\) là
\(F\left( x \right) = 3{x^3} + 5\).
\(F\left( x \right) = {x^3} - 5\).
\(F\left( x \right) = {x^3} + 5\).
\(F\left( x \right) = 6x + 5\).
Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = \sin x,\;y = \cos x\) và các đường thẳng \(x = 0,\;x = 7\)được tính bằng công thức
\(S = \int\limits_0^7 {( - \sin x + {\rm{cos}}x){\rm{d}}x} \).
\[S = \int\limits_0^7 {\left| {{\rm{sin}}x - {\rm{cos}}x} \right|} {\rm{d}}x\].
\[S = \int\limits_0^7 {({\rm{sin}}x - {\rm{cos}}x){\rm{d}}x} \].
\[S = \int\limits_0^7 {({\rm{sin}}x + {\rm{cos}}x){\rm{d}}x} \].
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong dây chuyền sản xuất sữa chua hiện đại của một nhà máy thực phẩm, từng giọt sữa chua âm thầm chuyển mình dưới tác động của hàng triệu vi khuẩn Lactic, những “nghệ nhân tí hon” kiến tạo vị chua thanh đặc trưng. Mật độ vi khuẩn (số triệu tế bào trên mỗi ml sữa chua) tại thời điểm \(t\) (giờ) được kí hiệu là \(N\left( t \right)\). Ban đầu (\(t = 0\) giờ), mật độ vi khuẩn đo được là \(N\left( 0 \right) = 10\) triệu tế bào/ml. Do sự thay đổi về nguồn dinh dưỡng (đường lactose giảm) và độ pH (axit lactic tăng) nên tốc độ thay đổi mật độ vi khuẩn \(N'\left( t \right)\) (đơn vị: triệu tế bào/ ml mỗi giờ) được mô hình hóa bởi công thức \(N'\left( t \right) = 18t - 3{t^2}\) (triệu tế bào/ml mỗi giờ) với \(t\) là thời gian tính bằng giờ (\(0 \le t \le 7\)).
a)\(N'\left( 1 \right) = 15\) triệu tế bào/ml giờ.
b)\(\int {N'\left( t \right){\rm{d}}t} = 9{t^2} - {t^3}\).
c) So với lúc ban đầu (\(t = 0\)), mật độ vi khuẩn đã tăng thêm 108 triệu tế bào/ml khi đến thời điểm \(t = 6\) giờ.
d) Tại thời điểm \(t = 7\) giờ, mật độ vi khuẩn trong 1 ml sữa chua là 108 triệu tế bào/ml.
Một robot tự hành ở một cảng vận chuyển công nghệ cao bắt đầu di chuyển từ vị trí nghỉ tại điểm A. Robot di chuyển như sau: Trong giai đoạn đầu, robot tăng tốc đều từ vận tốc \(0\,\,\left( {{\rm{m/s}}} \right)\) đến \(10\,\,\left( {{\rm{m/s}}} \right)\) trong thời gian chưa biết \({t_1}\) giây theo hàm số vận tốc \({v_1}\left( t \right) = at\) (\(a\) gọi là gia tốc trong giai đoạn này, \(a\,\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)). Sau đó, robot tiếp tục di chuyển với vận tốc không đổi trong 40 giây. Cuối cùng, robot giảm tốc đều từ \(10\,\,\left( {{\rm{m/s}}} \right)\) và dừng lại đúng tại băng chuyền điểm \(B\) với thời gian \({t_2}\) giây theo hàm vận tốc \({v_2}\left( t \right) = 10 - bt\)(\(b\)gọi là gia tốc trong giai đoạn này, \(b\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)). Toàn bộ quá trình vận chuyển diễn ra trong tổng thời gian là 70 giây.
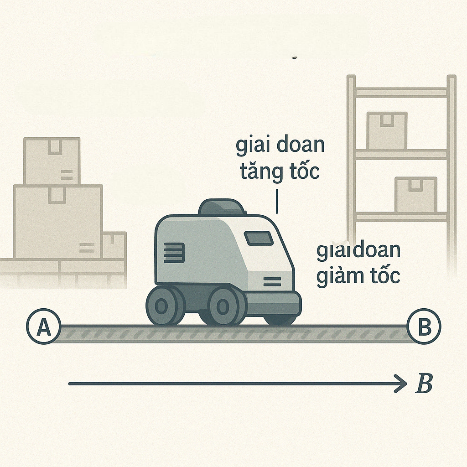
a) Nếu gia tốc \(a = 0,5\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), thời gian tăng tốc \({t_1}\) bé hơn \(21\) giây.
b) Nếu gia tốc \(b = 0,8\,\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), thời gian giảm tốc \({t_2}\) lớn hơn \(13\) giây.
c) \(a + b \le \,\frac{5}{4}\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\).
d) Tổng quãng đường mà robot đã di chuyển từ \(A\) đến \(B\) là \(550\,{\rm{m}}\).
Phần 3. Trắc nghiệm trả lời ngắn
Hai công ty, công ty A và công ty B, cùng ra mắt sản phẩm cạnh tranh thị trường mới vào cùng thời điểm. Thị phần được đo bằng số lượng khách hàng lũy kế.
Công ty A: Bắt đầu với 0 khách hàng. Trong giai đoạn đầu, chiến dịch marketing hiệu quả giúp tốc độ thu hút khách hàng mới của họ tăng dần theo thời gian, được mô tả bởi hàm \(f\left( t \right) = 2t + 7\) (nghìn khách hàng/tháng), với \(t\) là số tháng kể từ khi ra mắt.
Công ty B: Nhờ có uy tín từ trước, họ bắt đầu với 10 nghìn khách hàng đặt trước sản phẩm. Sau đó, họ duy trì một tốc độ thu hút khách hàng mới ổn định là 10 nghìn khách hàng/tháng.
Hỏi sau khoảng bao nhiêu tháng kể từ khi ra mắt, tổng số lượng khách hàng lũy kế của công ty A bằng tổng số lượng khách hàng lũy kế của công ty B (tính cả 10 nghìn khách hàng ban đầu)?
Một hoa văn hình tròn tâm O, ngoại tiếp tam giác đều ABC có cạnh \[AB = 2\sqrt 3 \,{\rm{cm}}.\] Đường cong qua ba điểm A,B,C là một phần của parabol (xem hình vẽ).![Một hoa văn hình tròn tâm O, ngoại tiếp tam giác đều ABC có cạnh \[AB = 2\sqrt 3 \,{\rm{cm}}.\] Đường cong qua ba điểm A,B,C là một phần của parabol (xem hình vẽ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/7-1759412289.png)
Tính diện tích của phần hình phẳng giới hạn bởi đường tròn và parabol (phần không gạch) theo đơn vị cm2 (kết quả làm tròn đến chữ số thập phân thứ hai).
Một kiến trúc sư chịu trách nhiệm thiết kế một tòa nhà cao 30 mét. Mặt cắt ngang tại mọi độ cao, vuông góc với trục thẳng đứng, luôn là một hình vuông (xem hình vẽ).
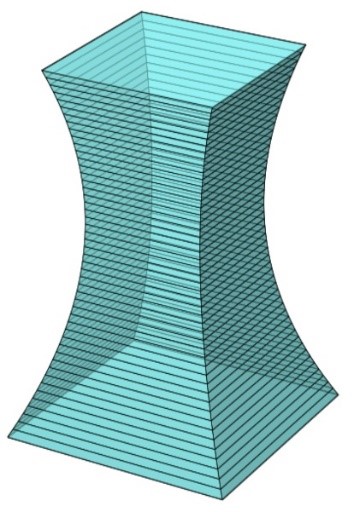
Mặt đáy tòa nhà là hình vuông có cạnh \({L_0} = 26\;{\rm{m,}}\) mặt đỉnh là hình vuông có cạnh \({L_{30}} = 20\;{\rm{m}}{\rm{.}}\)Mặt cắt ngang tại vị trí hẹp nhất của tòa nhà: Hình vuông có cạnh \({L_{min}} = 13,75\;{\rm{m}}{\rm{.}}\) Mặt cắt của tòa nhà theo mặt phẳng đứng chứa đường chéo đáy có dạng là hình phẳng giới hạn bởi hai đường cong parabol đối xứng nhau qua trục thẳng đứng đi qua tâm đáy của tòa nhà. Tính thể tích của tòa nhà đó (làm tròn đến hàng đơn vị, đơn vị tính: mét khối).


