35 câu hỏi
Một cung tròn có độ dài bằng bán kính. Khi đó số đo bằng radian của cung tròn đó là
1;
2;
\(\pi \);
\(2\pi \).
Trong mặt phẳng tọa độ \(Oxy,\)cho đường tròn lượng giác như hình vẽ bên dưới.
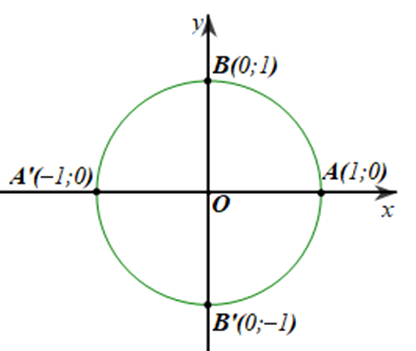
Hỏi góc lượng giác nào sau đây có số đo là \( - 90^\circ \)?
\(\left( {OA,OB} \right)\);
\(\left( {OA,OA'} \right)\);
\(\left( {OA,OB'} \right)\);
\(\left( {OA,OA} \right)\).
Một góc lượng giác \(\alpha \) có điểm cuối ở góc phần tư thứ II thì
\(\left| {\sin \alpha } \right| = - {\rm{sin}}\alpha \);
\(\sqrt {{\rm{si}}{{\rm{n}}^2}\alpha } = {\rm{sin}}\alpha \);
\(\sqrt {{\rm{co}}{{\rm{s}}^2}\alpha } = {\rm{cos}}\alpha \);
\(\tan \alpha > 0\).
Đơn giản biểu thức \(A = \cos \left( {\frac{{9\pi }}{2} - \alpha } \right) + \sin \left( {\alpha - \pi } \right)\) ta được
\(A = \cos \alpha + \sin \alpha \);
\(A = 2\sin \alpha \);
\(A = \sin \alpha \cos \alpha \);
\(A = 0\).
Cho góc \(\alpha \) thỏa mãn \({\rm{tan}}\alpha + {\rm{cot}}\alpha = 2\). Giá trị của biểu thức \(P = {\rm{ta}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{t}}^2}\alpha \) là
\(P = 1\);
\(P = 2\);
\(P = 3\);
\(P = 4\).
Khẳng định nào sau đây đúng?
\({\rm{sin}}\left( {2030a} \right) = 2030{\rm{sin}}a.{\rm{cos}}a\);
\({\rm{sin}}\left( {2030a} \right) = 2030{\rm{sin}}\left( {1015a} \right){\rm{.cos}}\left( {1015a} \right)\);
\({\rm{sin}}\left( {2030a} \right) = 2{\rm{sin}}a{\rm{cos}}a\);
\({\rm{sin}}\left( {2030a} \right) = 2{\rm{sin}}\left( {1015a} \right){\rm{.cos}}\left( {1015a} \right)\).
Hàm số \(y = f\left( x \right)\) (có tập xác định \(D\)) là hàm số lẻ nếu với \(\forall x \in D\) thì \( - x \in D\) và
\[f\left( { - x} \right) = f\left( x \right)\];
\[f\left( { - x} \right) = - f\left( x \right)\];
\[f\left( { - x} \right) = f\left( {\pi x} \right)\];
\[f\left( { - x} \right) = - f\left( {\pi x} \right)\].
Hàm số \(y = \sin x\) là hàm số tuần hoàn với chu kì
\(\pi \);
\(2\pi \);
\(\frac{1}{2}\pi \);
\(3\pi \).
Trong các hàm số \(y = \sin x\), \(y = \cos x\), \(y = \tan x\), \(y = \cot x\), có bao nhiêu hàm số đồng biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?
0;
1;
2;
3.
Tập xác định \(D\) của hàm số \(y = \sqrt {1 - {\rm{sin}}2x} - \sqrt {1 + {\rm{sin}}2x} \) là
\(D = \emptyset \);
\(D = \mathbb{R}\);
\(D = \left[ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi } \right],k \in \mathbb{Z}\);
\(D = \left[ {\frac{{5\pi }}{6} + k2\pi ;\frac{{13\pi }}{6} + k2\pi } \right],k \in \mathbb{Z}\).
Tập giá trị \(T\) của hàm số \[y = 5 - 3\sin x\] là
\(T = \left[ { - 1;1} \right]\);
\(T = \left[ { - 3;3} \right]\);
\(T = \left[ {2;8} \right]\);
\(T = \left[ {5;8} \right]\).
Tất cả nghiệm của phương trình \(\tan x = \tan \frac{\pi }{{11}}\) là
\(x = \frac{\pi }{{11}} + k2\pi ,k \in \mathbb{Z}\);
\(x = \frac{\pi }{{11}} + k\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{{11}} + k2\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{{11}} + k\pi ,k \in \mathbb{Z}\).
Phương trình \(\cos x = 0\) có nghiệm là
\(x = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\);
\(x = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Số nghiệm thuộc đoạn \(\left[ {\pi ;2\pi } \right]\) của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = 1\) là
0;
1;
2;
3.
Phương trình \(\cot 3x = - \frac{{\sqrt 3 }}{3}\)có nghiệm là
\(x = - \frac{\pi }{3} + k\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{9} + k\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{9} + k2\pi ,k \in \mathbb{Z}\);
\(x = - \frac{\pi }{9} + k\frac{\pi }{3},k \in \mathbb{Z}\).
Dãy số nào dưới đây là dãy số nguyên tố nhỏ hơn \[10\] theo thứ tự tăng dần?
\(0;1;2;3;5;7\);
\(1;2;3;5;7\);
\(2;3;5;7\);
\(1;3;5;7\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {2^n}.\) Số hạng \({u_{n + 1}}\) là
\[{u_{n + 1}} = {2^n}.2\];
\[{u_{n + 1}} = {2^n} + 1\];
\[{u_{n + 1}} = 2\left( {n + 1} \right)\];
\[{u_{n + 1}} = {2^n} + 2\].
Trong các dãy số sau, dãy số nào không bị chặn?
\[\left( {{u_n}} \right):{u_n} = \cos \left( {2n} \right)\];
\[\left( {{v_n}} \right):{v_n} = \frac{{2n + 5}}{{5n + 2}}\];
\[\left( {{k_n}} \right):{k_n} = {n^2} + 4n + 9\];
\[\left( {{a_n}} \right):{a_n} = {\left( { - 1} \right)^n}\].
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 8\). Công sai của cấp số cộng đã cho bằng
\( - 6\);
4;
6;
10.
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = - 5\) và \(d = 3.\)Mệnh đề nào sau đây đúng?
\({u_{15}} = 34\);
\({u_{15}} = 45\);
\({u_{13}} = 31\);
\({u_{10}} = 35\).
Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế?
\(1635\);
\(1792\);
\(2055\);
\(3125\).
Cho bốn điểm \(A,\,B,\,C,\,D\) không cùng nằm trong một mặt phẳng. Trên \(AB,\,AD\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \(MN\) cắt \(BD\) tại \(I\). Điểm \(I\) không thuộc mặt phẳng nào sao đây?
\[\left( {BCD} \right)\];
\[\left( {ABD} \right)\];
\[\left( {CMN} \right)\];
\[\left( {ACD} \right)\].
Cho bốn điểm \[A,\,B,\,C,\,D\] không đồng phẳng. Giao tuyến của hai mặt phẳng \[\left( {ABC} \right)\] và \[\left( {ACD} \right)\] là
\[AB\];
\[AC\];
\[BC\];
\[AD\].
Hình chóp có 16 cạnh thì có bao nhiêu mặt?
7;
8;
9;
10.
Khẳng định nào sau đây là đúng?
Hình chóp tứ giác là một hình tứ diện;
Hình tứ diện đều có mặt đáy là tam giác đều;
Mặt bên của tứ diện đều là hình tam giác cân;
Cả A, B, C đều đúng.
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AD,BC\), điểm \(G\) là trọng tâm của tam giác \(BCD\). Giao điểm của đường thẳng \(MG\) với mặt phẳng \(\left( {ABC} \right)\) là
giao điểm của \(MG\) và \(BC\);
giao điểm của \(MG\) và \(AC\);
giao điểm của \(MG\) và \(AN\);
giao điểm của \(MG\) và \(AB\).
Cho tứ diện \[ABCD.\] Gọi \[E\] và \[F\] lần lượt là trung điểm của \[AB\] và \[CD\]; \[G\] là trọng tâm tam giác \[BCD.\] Giao điểm của đường thẳng \[EG\] và mặt phẳng \[\left( {ACD} \right)\] là
Điểm \[F\];
Giao điểm của đường thẳng \[EG\] và \[AF\];
Giao điểm của đường thẳng \[EG\] và \[AC\];
Giao điểm của đường thẳng \[EG\] và \[CD\].
Cho hình chóp \[S.ABCD\]có đáy \[ABCD\] là hình bình hành. Hỏi cạnh \[CD\] chéo với tất cả các cạnh nào của hình chóp?
\[SA;\,AB\];
\[SA;\,SB\];
\[SB;AB\];
\[SB;\,AD\].
Trong không gian cho các mệnh đề sau:
(I) Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì song song với nhau.
(II) Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
(III) Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy song song với nhau.
(IV) Qua điểm \(A\) không thuộc đường thẳng \[d\], kẻ được đúng một đường thẳng song song với \[d\].
Số mệnh đề đúng là
0;
1;
2;
3.
Trong không gian, cho ba đường thẳng \(a,\,\,b,\,\,c\). Trong các mệnh đề sau mệnh đề nào đúng?
Nếu \(a\) và \(b\) không cắt nhau thì \(a\) và \(b\) song song;
Nếu \(b\) và \(c\) chéo nhau thì \(b\) và \(c\) không cùng thuộc một mặt phẳng;
Nếu \(a\) và \(b\) cùng chéo nhau với \(c\) thì \(a\) song song với \(b\);
Nếu \(a\) và \(b\) cắt nhau, \(b\) và \(c\) cắt nhau thì \(a\) và \(c\) cắt nhau.
Cho hình chóp \[S.ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[AB\] và \[BC\]. Giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SIJ} \right)\] là một đường thẳng song song với
đường thẳng \[AD\];
đường thẳng \[AB\];
đường thẳng \[AC\];
đường thẳng \[BD\].
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) trong không gian. Có bao nhiêu vị trí tương đối của \(a\) và \(\left( P \right)\)?
1;
2;
3;
4.
Cho mặt phẳng \[\left( \alpha \right)\] và đường thẳng \[d \not\subset \left( \alpha \right)\]. Khẳng định nào sau đây là sai?
Nếu \[d\,{\rm{//}}\,\left( \alpha \right)\] thì trong \[\left( \alpha \right)\] tồn tại đường thẳng \[\Delta \] sao cho \[\Delta \,{\rm{//}}\,d\];
Nếu \[d\,{\rm{//}}\,\left( \alpha \right)\] và \[b \subset \left( \alpha \right)\] thì \[b\,{\rm{//}}\,d\];
Nếu \[d \cap \left( \alpha \right) = A\] và \[d' \subset \left( \alpha \right)\] thì \[d\] và \[d'\] hoặc cắt nhau hoặc chéo nhau;
Nếu \[d\,{\rm{//}}\,c\,;\,\,c \subset \left( \alpha \right)\] thì \[d\,{\rm{//}}\,\left( \alpha \right)\].
Cho tứ diện \(ABCD\), gọi \({G_1},{G_2}\) lần lượt là trọng tâm tam giác \(BCD\) và \(ACD.\) Mệnh đề nào sau đây sai?
\({G_1}{G_2}\,{\rm{//}}\,\left( {ABD} \right)\);
Ba đường thẳng \(B{G_1},A{G_2}\) và \(CD\)đồng quy;
\({G_1}{G_2}\,{\rm{//}}\,\left( {ABC} \right)\);
\({G_1}{G_2} = \frac{2}{3}AB\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\), gọi \(I\) là trung điểm cạnh \(SC\). Mệnh đề nào sau đây sai?
Đường thẳng \(IO\) song song với mặt phẳng \(\left( {SAD} \right)\);
Đường thẳng \(IO\) song song với mặt phẳng \(\left( {SAB} \right)\);
Mặt phẳng \(\left( {IBD} \right)\) cắt mặt phẳng \(\left( {SAC} \right)\) theo giao tuyến \(OI\);
Mặt phẳng \(\left( {IBD} \right)\) cắt hình chóp \(S.ABCD\) theo một thiết diện là tứ giác.
Gợi ý cho bạn
Xem tất cảĐề kiểm tra Cuối kì 1 Toán 11 Cánh Diều có đáp án - Đề 02
Đề kiểm tra Cuối kì 1 Toán 11 Cánh Diều có đáp án - Đề 01