Trắc nghiệm chuyên đề Toán 8 Chủ đề 7: Ôn tập và kiểm tra có đáp án
45 câu hỏi
Cho AB = 6 cm, AC = 18 cm, tỉ số hai đoạn thẳng AB và AC là?
1/2
1/3
2
3
Tìm độ dài x cho hình vẽ sau biết MN//BC
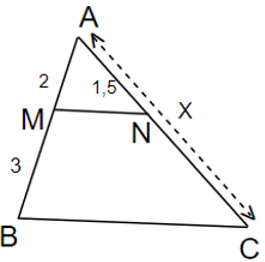
x = 2,75
x = 5
x = 3,75
x = 2,25
Cho AB/A'B' = CD/C'D'
⇔ AB.C'D' = A'B'.CD ( I )
⇔ AB/CD = A'B'/C'D' ( II )
( I ),( II ) đều sai.
( I ),( II ) đều đúng.
Chỉ có ( I ) đúng
Chỉ có ( II ) đúng.
Cho các đoạn thẳng AB = 6cm, CD = 4cm, PQ = 8cm, EF = 10cm, MN = 25mm, RS = 15mm. Hãy chọn phát biểu đúng trong các phát biểu sau?
Đoạn AB và PQ tỉ lệ với hai đoạn thẳng EF vs RS.
Hai đoạn thẳng AB và RS tỉ lệ với hai đoạn thẳng EF và MN
Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng PQ và EF
Cả 3 phát biểu đều sai.
Cho các đoạn thẳng AB = 8cm, AC = 6cm, MN = 12cm, PQ = x cm. Tìm x để AB và CD tỉ lệ với MN và PQ?
x = 18 mm
x = 9 cm
x = 0,9 cm
x = 2 cm
Tính x trong trường hợp sau:
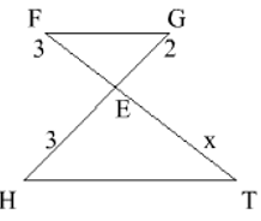
x = 4,5
x = 3
x = 2
Cả 3 đáp án trên đều sai
Cho hình bên. Chọn câu trả lời đúng?
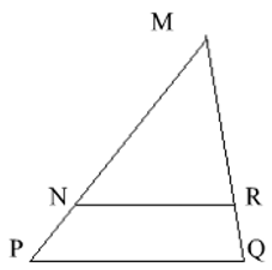
MN/NP = RQ/MR ⇒ NR//PQ
MN/MP = MR/RQ ⇒ NR//PQ
MN/NP = MR/MQ ⇒ NR//PQ
Cả 3 đáp án đều sai.
Cho hình bên. Chọn câu trả lời đúng?
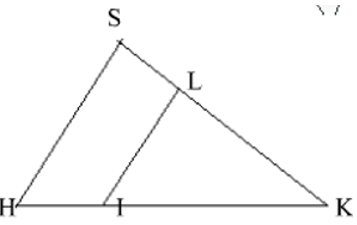
SL/LK = HI/HK ⇒ SH//LI
SL/SK = HI/HK ⇒ SH//LI
HI/HK = LK/SL ⇒ SH//LI
HK/HI = SL/SK ⇒ SH//LI
Cho Δ ABC có độ dài các cạnh như hình vẽ. Kết quả nào sau đây đúng?
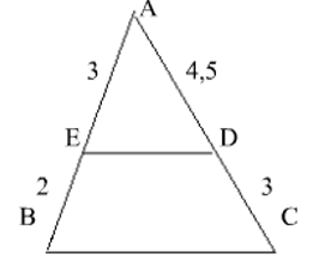
ED/BC = 1,5
ED/BC = 3/7,5
ED/BC = 3 5
Cả 3 đáp án đều sai.
Cho Δ ABC vuông tại A có AB = 3 cm, BC = 5 cm, AD là đường phân giác của Δ ABC. Chọn phát biểu đúng?
BD = 20/7 cm; CD = 15/7 cm
BD = 15/7 cm; CD = 20/7 cm
BD = 1,5 cm; CD = 2,5 cm
BD = 2,5 cm; CD = 1,5 cm
Cho Δ ABC có BD là đường phân giác, AB = 8 cm, BC = 10 cm, AC = 6cm. Chọn phát biểu đúng?
DA = 8/3 cm, DC = 10/3 cm
DA = 10/3 cm, DC = 8/3 cm
DA = 4 cm, DC = 2 cm
DA = 3,5 cm, DC = 2,5 cm
Cho Δ ABC có Aˆ = 1200 , AD là đường phân giác. Chọn phát biểu đúng?
1/AD + 1/AC = 1/AB
1/AB + 1/AC = 1/AD
1/AB + 1/AC = 2/AD
1/AB + 1/AC + 1/AD = 1
Cho Δ ABC. Tia phân giác góc trong của góc A cắt BC tại D. Cho AB = 6, AC = x, BD = 9, BC = 21. Tính kết quả đúng của độ dài cạnh x ?
x = 14
x = 12
x = 8
x = 6
Cho Δ ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác BACˆ cắt BC tại D. Tỉ số diện tích của Δ ABD và Δ ACD là?
1/4
1/2
3/4
1/3
Ta có Δ MNP ∼ Δ ABC thì
MN/AB = MP/AC
MN/AB = MP/BC
MN/AB = NP/AC
MN/BC = NP/AC
Cho Δ ABC ∼ Δ A'B'C' có AB = 3A'B'. Kết quả nào sau đây sai?
Aˆ = A'ˆ ; Bˆ = B'ˆ
A'C' = 1/3 AC
AC/BC = A'C'/B'C' = 3
AB/A'B' = AC/A'C' = BC/B'C'
Cho Δ ABC ∼ Δ A'B'C' có AB/A'B' = 2/5 . Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng?
Chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.
Chu vi của Δ ABC là 50cm, chu vi của Δ A'B'C' là 20cm.
Chu vi của Δ ABC là 45cm, chu vi của Δ A'B'C' là 75cm.
Δ A'B'C'
Cho Δ ABC có AB = 8cm, AC = 6cm, BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
4cm; 3cm
7,5cm; 10cm
4,5cm; 6cm
15cm; 20cm
Cho Δ ABC ∼ Δ DEF có tỉ số đồng dạng là k = 3/5 , chu vi của Δ ABC bằng 12cm. Chu vi của Δ DEF là?
7,2cm
20cm
3cm
17/3 cm
Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
Δ ABC ∼ Δ DEF
ABCˆ = EFDˆ
ACBˆ = ADFˆ
ACBˆ = DEFˆ
Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
Δ RSK ∼ Δ PQM
Δ RSK ∼ Δ MPQ
Δ RSK ∼ Δ QPM
Δ RSK ∼ Δ QMP
Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
RSKˆ = PQMˆ
RSKˆ = PMQˆ
RSKˆ = MPQˆ
RSKˆ = QPMˆ
Chọn câu trả lời đúng?
Δ ABC, Δ DEF; AB/DE = AC/DF ;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Δ ABC, Δ DEF; AB/DE = AC/DF ;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
Δ ABC, Δ DEF; AB/DE = AC/DF ;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
Δ ABC, Δ DEF; AB/DE = AC/DF ;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ . Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
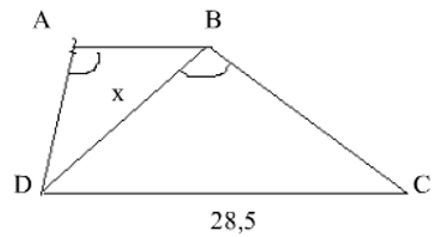
17,5
18
18,5
19
Cho EF/GH = MN/PQ . Chọn phát biểu sai trong các phát biểu sau?
EF.PQ = GH.MN
EF/GH = (EF + MN )/( GH + PQ )
EF/( EF + GH ) = MN/( MN + PQ )
EF/( EH + GH ) = MN/( MN + PQ )
Cho Δ ABC có AB = 15cm, AC = 20cm, BC = 25cm, đường phân giác góc A cắt BC tại D. Tính độ dài đoạn BD (theo cm)
10
10 ( 5/7 )
14
14 (2/7 )
Cho tam giác ABC có các đường phân giác là AD, BE, CF. Chọn phát biểu đúng trong các phát biểu sau?
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm, AD là đường phân giác của góc A ( D ∈ BC ). Kết quả nào sau đây đúng?
DB = 4cm
DC = 7cm
DB = 30/7 cm
DC = DB
Cho Δ ABC ∼ Δ A'B'C' có tỉ số đồng dạng là k = 5/9 . P và P' lần lượt là chu vi của tam giác ABC và tam giác A'B'C', biết P + P' = 28. Tính P và P'.
P = 16cm, P' = 12cm
P = 12cm, P' = 16cm
P = 10cm, P' = 18cm
P = 14cm, P' = 14cm
Nếu hai tam giác DEF và SKL có DF/SL = EF/KL và Fˆ = Lˆ thì:
DF/SL = DE/KL
DF/SL = DE/SK
DF/SK = DE/SL
DF/KL = EF/SK
Cho đoạn thẳng AB = 10 cm
a) Trên đoạn thẳng AB lấy điểm C sao cho CA/CB = 3/2 . Tính độ dài đoạn CB.
b) Trên tia đối của tia BA lấy điểm D sao cho DA/DB = 3/2 . Tính độ dài đoạn CD.
Tính giá trị của x trên hình vẽ đã có:
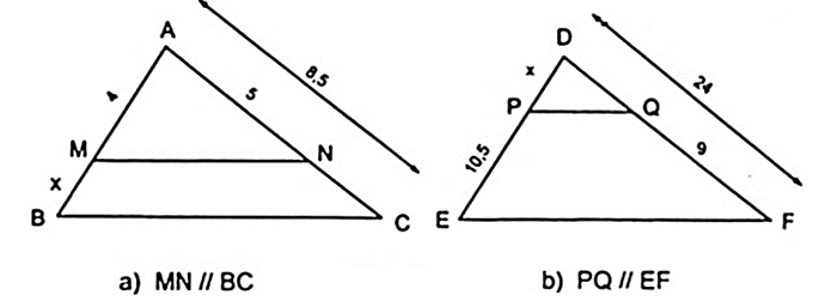
Tính độ dài x, y trong các hình bên
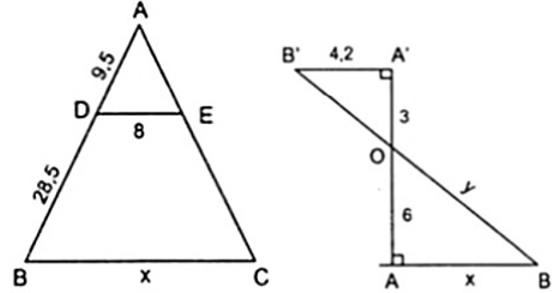
:
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.

Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.
Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3 , EA/EB = 5/6 . Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng k1 , Δ A''B''C'' ∼ Δ ABC theo tỉ số đồng dạng là k2 . Hỏi Δ A''B''C'' ∼ Δ A'B'C' và Δ A'B'C' ∼ Δ ABC đồng dạng theo tỉ số nào?
Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5
a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết hiệu chu vi của hai tam giác trên là 40dm. Tính chu vi của hai tam giác đã cho
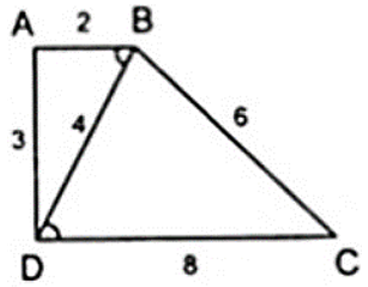
Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Chân đường cao AH chia cạnh huyền BC thành hai đoạn thẳng có độ dài lần lượt là 25 cm và 36 cm. Tính chu vi và diện tích của tam giác đó.
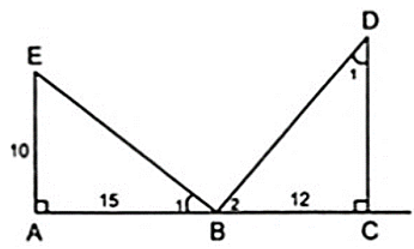
Cho hình vẽ như bên, biết EBAˆ = BDCˆ
a) Trong hình vẽ có bao nhiêu tam giác vuông? Kể tên các tam giác vuông đó.
b) Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất)
c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD
Cho B nằm trên đoạn thẳng AC, AB = 6cm, BC = 24cm. Vẽ về một phía của AC các tia Ax và Cy vuông góc với AC. Trên tia Ax lấy điểm E sao cho EB = 10cm, trên tia Cy lấy điểm D sao cho MD = 30cm. Chứng minh EBDˆ = 900 .
Cho tam giác ABC. Qua D là điểm trên cạnh BC lần lượt kẻ các đường thẳng song song với AB, AC chúng cắt AB, AC theo thứ tự ở E và F. Biết diện tích của tham giác BED là 16cm2 , diện tích tam giác FDC bằng 25cm2 . Tính SABC
Cho tam giác ABC vuông tại A, đường cao AH có AB = 15cm;AC = 20cm. Tia phân giác của góc HAB cắt HB tại D, tia phân giác của góc HAC cắt HC tại E. Tính độ dài các đoạn AH, HD và HE.
Cho tam giác ABC có BC = a; CA = b; AB = c. Các đường phân giác AD, BE, CF cắt nhau tại I. Chứng minh rằng: