Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 2)
15 câu hỏi
Phần I: Trắc nghiệm
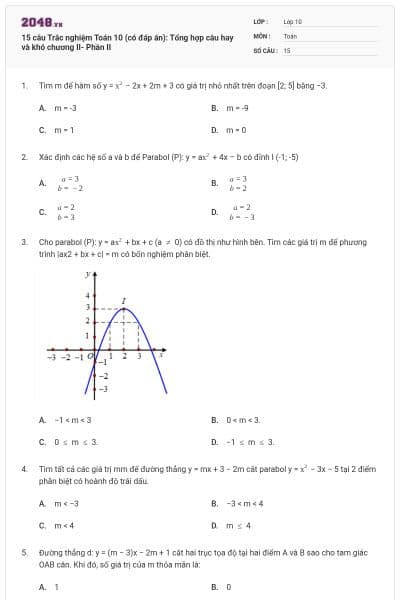
Điều kiện xác định của bất phương trình là:
x
x
Tập nghiệm của bất phương trình 2x(2 - x) ≥ 2 - x là:
S = [;)
S = (;][2;)
S = [0;)
[;2]
Với giá trị nào của m thì bất phương trình x + m - 1 < x vô nghiệm?
m = 1 và m = -1
m = 1
m = -1
m ∈ ∅
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
2 + 3y > 0
+ < 2
x + ≥ 0
x + y ≥ 0
Phương trình - (m + 1)x + 1 = 0 có nghiệm khi và chỉ khi
m > 1
–3 < m < 1
m ≤ -3 hoặc m ≥ 1
-3 ≤ m ≤ 1
Tập nghiệm của bất phương trình là
(;1)
(;)
(1;)
(;)(1;)
Phương trình (m + 2) - 3x + 2m - 3 = 0 có hai nghiệm trái dấu khi và chỉ khi
m<-2
-2<m<
(;]
[;)
Cho hệ bất phương trình:
Hệ bất phương trình đã cho có nghiệm khi và chỉ khi
m < –5
m > –5
m > 5
m < 5
Với x thuộc tập hợp nào dưới đây thì f(x) = x(5x + 2) - x( + 6) không dương
(;1] ∪ [4;)
[1;4]
(1;4)
[0;1] ∪ [4;)
Tập nghiệm của bất phương trình
S = (-1/2;2)
S = (;-1/2)(2;)
S = (;-1/2)[2;)
S = (-1/2;2]
Với giá trị nào của m thì phương trình: (m - 1) - 2(m - 2)x + m - 3 = 0 có hai nghiệm x1, x2 và x1 + x2 + x1x2 < 1?
1 < m < 2
1 < m < 3
m > 2
m > 2
Bất phương trình : |3x - 3| ≤ |2x + 1| có tập nghiệm là
[4;)
(;]
[;4]
(;4]
Phần II: Tự luận
Giải các bất phương trình:
a)
b)
c)
Cho phương trình: - 2(m - 3)x + 5 - m = 0
a) Giải phương trình khi m = 1.
b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn x1 < x2 < 1.
Chứng minh rằng , với mọi a, b ≥ 0