Đề cương ôn tập giữa kì 1 Toán 7 Chân trời sáng tạo cấu trúc mới (Tự luận) có đáp án - Phần 3

Cho hình vẽ bên. Biết \(\widehat {xOz} = 97^\circ ,\,\,\widehat {tOu} = 82^\circ \) và tia \(Oz\) là tia phân giác của góc \(\widehat {tOu}\).

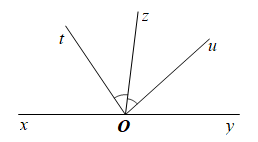
a) Vẽ lại hình và kể tên các cặp góc kề bù (không tính góc bẹt) có trong hình vẽ.

b) Tính số đo của góc \(\widehat {tOz},\,\,\widehat {tOy}\).

Cho góc bẹt \(xOy\). Vẽ ba tia \(Om,\,\,On,\,\,Oz\) sao cho tia \(Om\) nằm giữa hai tia \[Ox,\,\,Oz\] và \(\widehat {xOm} = 50^\circ ,\,\,\widehat {xOz} = 130^\circ \). Vẽ tia \(On\) là tia đối của tia \(Oz.\)

a) Vẽ hình và kể tên các góc kề bù với góc \(xOz\) có trong hình vẽ.

b) Tính số đo của góc \(yOz.\) Giải thích tại sao tia \[Ox\] là tia phân giác của góc \(mOn.\)

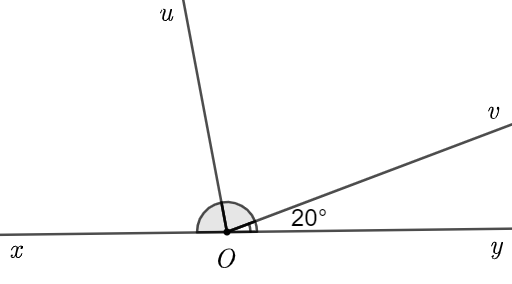
Cho hình vẽ sau. Biết \(\widehat {xOy}\) là góc bẹt và \(Ou\) là tia phân giác của \(\widehat {xOv}\). Tính số đo \(\widehat {uOv}\).

Cho tam giác \(ABC\) vuông tại \(A\). Qua đỉnh \(B\) của tam giác kẻ đường thẳng \(ab\) vuông góc với cạnh \(AB\)(\(AC,\,\,Bb\) thuộc cùng một nửa mặt phẳng có bờ là đường thẳng chứa cạnh \(AB\)).

a) Chứng minh \[a\,b\parallel AC\].

b) Biết \[\widehat {CBb} = 35^\circ \]. Tính số đo các góc trong tam giác \(ABC\).

Đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\) lần lượt tại hai điểm \(M\) và \(N\). Đường thẳng \(d\) cắt hai đường thẳng \(a\) và \(b\) lần lượt tại hai điểm \(P\) và \(Q\) (như hình vẽ). Biết \({\widehat M_1} = 55^\circ ;\,\,{\widehat N_1} = 55^\circ ;\,\)\(\,{\widehat Q_1} = 125^\circ .\)

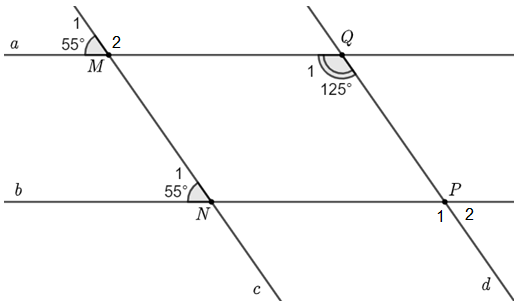
a) Vẽ lại hình và viết giả thiết, kết luận của bài toán.

b) Chứng minh \[MQ\parallel NP & ;\,\,MN\parallel PQ\].

c) Tìm số đo \({\widehat P_2}\).

Cho hình vẽ, biết \[AB\,{\rm{//}}\,xy,\] \(\widehat {BAI} = 45^\circ \), \(\widehat {AIF} = 105^\circ \).

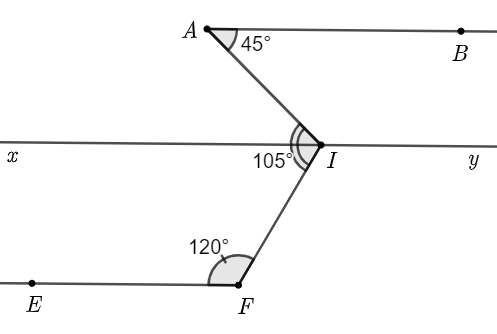
a) Vẽ lại hình và viết giả thiết, kết luận của bài toán.

b) Tính số đo \(\widehat {FIx}\) và \(\widehat {FIy}\).

c) Chứng minh \[AB\,{\rm{//}}\,EF\].