Đề cương ôn tập cuối kì 1 Toán 6 Kết nối tri thức cấu trúc mới có đáp án
76 câu hỏi
A. Bài tập trắc nghiệm
1. Trắc nghiệm nhiều phương án lựa chọn
Khoanh tròn chữ cái đứng trước câu trả lời đúng.
Tập hợp \(A\) gồm các số tự nhiên lớn hơn 7 và không lớn hơn 12. Tập hợp \(A\) được viết bằng cách liệt kê các phần tử là
\(A = \left\{ {7;\,\,8;\,\,9;\,\,10;\,\,11;\,\,12} \right\}\).
\(A = \left\{ {8;\,\,9;\,\,10;\,\,11} \right\}\).
\(A = \left\{ {8;\,\,9;\,\,10;\,\,11;\,\,12} \right\}\).
\(A = \left\{ {7;\,\,8;\,\,9;\,\,10;\,\,11} \right\}\).
Cho tập hợp \(B = \left\{ {x \in \mathbb{N}*|\,\,x \le 5} \right\}\). Khẳng định nào sau đây là sai?
\(0 \in B\).
\(5 \in B\).
\(6 \notin B\).
Tập hợp \(B\) có 5 phần tử.
Ba số nào sau đây là ba số tự nhiên liên tiếp tăng dần?
\(a - 1,\,\,a,\,\,a + 1\,\,\left( {a \in \mathbb{N}} \right)\).
\(a,\,\,a + 1,\,\,a + 2\,\,\left( {a \in \mathbb{N}} \right)\).
\(2a,\,\,3a,\,\,4a\,\,\left( {a \in \mathbb{N}} \right)\).
\(a + 1,\,\,a,\,\,a - 1\,\,\left( {a \in \mathbb{N}} \right)\).
Số 22 viết bằng số La Mã là
IIXX.
XIIX.
XXII.
XX.
Kết quả của lũy thừa nào sau đây là sai?
\({1^{1\,\,000}} = 1\).
\(1\,\,{000^0} = 1\).
\({0^{1\,\,000}} = 0\).
\[{0^{3\,\,000}} = 1\].
Các chữ số \(x,\,\,y\) thích hợp điền vào \(*\) để \(\overline {4x6y} \) chia hết cho \(2,\,\,5,\,\,9\) là
\(x = 5;\,\,y = 0\).
\(x = 0;\,\,y = 5\).
\(x = 8;\,\,y = 0\).
\(x = 0;\,\,y = 8\).
Điều kiện của số tự nhiên \(x\) để biểu thức \(A = 20 + 35 - 10 + x\) chia hết cho 5 là
\(x\) là số tự nhiên chẵn.
\(x\) là số tự nhiên lẻ.
\(x\) là bội của \(5\).
\(x \in \left\{ {0;\,\,5} \right\}\).
Trong các số \(0,\,\,1,\,\,2,\,\,4,\,\,7,\,\,28,\,\,29,\,\,31\) có bao nhiêu số nguyên tố?
3.
4.
5.
6.
Khi phân tích \(160\) thành tích các thừa số nguyên tố thì số mũ của \(2\) là
3.
4.
5.
6.
Tập hợp các ước nguyên tố của 18 là
\(\left\{ {1;\,\,2;\,\,3} \right\}\).
\(\left\{ {2;\,\,3;\,\,9} \right\}.\)
\(\left\{ {1;\,\,2;\,\,3;\,\,9;\,\,18} \right\}\).
\(\left\{ {2;\,\,3} \right\}\).
Cần ít nhất bao nhiêu xe 36 chỗ ngồi để chở hết 300 cổ động viên của đội bóng?
7 xe.
8 xe.
9 xe.
10 xe.
Nếu \(a \vdots m\), \(b \vdots m\) và \(m \in \mathbb{N}*\) thì
\(m\) là bội chung của \(a\) và \(b\).
\(m\) là ước chung của \(a\) và \(b\).
\(m = \)ƯCLN\(\left( {a,\,\,b} \right)\).
\(m = \)BCNN\(\left( {a,\,\,b} \right)\).
Cho \(a = {2^3} \cdot 3 \cdot 7\) và \(b = {2^2} \cdot {3^4} \cdot 5\) thì ƯCLN\(\left( {a,\,\,b} \right)\) là
\(12\).
\(24\).
\(60\).
\(420\).
Cho \(a = {2^4} \cdot 7\) và \(b = {2^2} \cdot 3 \cdot 7\) thì BCNN\(\left( {a,\,\,b} \right)\) là
\(21\).
\(28\).
\(112\).
\(336\).
Cho số tự nhiên \(a\) vừa là ước của \(20\) vừa là bội của \(5.\) Có bao nhiêu số \(a\) thỏa mãn?
1.
2.
3.
4.
Cho tập hợp \(C = \left\{ {...;\,\, - 4;\,\, - 2;\,\,0;\,\,2;\,\,4;\,\,...} \right\}\). Cách viết nào sau đây là đúng?
\(C = \left\{ {x \in \mathbb{Z}|x = 2k,\,\,k \in \mathbb{N}*} \right\}\).
\(C = \left\{ {x \in \mathbb{Z}|x = - 2k,\,\,k \in \mathbb{N}} \right\}\).
\(C = \left\{ {x \in \mathbb{Z}|x = 2k,\,\,k \in \mathbb{Z}} \right\}\).
\(C = \left\{ {x \in \mathbb{Z}|x = - 2k,\,\,k \in \mathbb{N}} \right\}\).
Nước đóng băng ở nhiệt độ dưới 0℃ trở xuống. Ở nhiệt độ –10℃ và 3℃. Trạng thái của nước lần lượt là
Đóng băng và lỏng
Đóng băng và đóng băng
Lỏng và đóng băng
Lỏng và lỏng
Sắp xếp các số nguyên \[2;\,\, - 17;\,\,5;\,\,1;\,\, - 2;\,\,0\] theo thứ tự giảm dần là
\[5;\,\,2;\,\,1;\,\,0;\,\, - 2;\,\, - 17\].
\[ - 17;\,\, - 2;\,\,0;\,\,1;\,\,2;\,\,5\].
\[5;\,\,2;\,\,1;\,\,0;\,\, - 17;\,\, - 2\].
\[ - 2;\,\, - 17;\,\,0;\,\,1;\,\,2;\,\,5\].
Tổng các số nguyên thỏa mãn \( - 10 < x \le 13\) là:
\[36\].
\[47\].
\(23\).
\[46\].
Số đối của \( - \left( { - 21} \right)\) là
\(12\).
\( - 12\).
\( - 21\).
\(21\).
Vào một ngày tháng một ở Moscow (Liên Bang Nga), buổi sáng nhiệt độ là \( - 5^\circ {\rm{C}}\), buổi trưa nhiệt độ tăng thêm \(2^\circ {\rm{C}}\), ban đêm nhiệt độ giảm \(4^\circ {\rm{C}}\). Hỏi nhiệt độ đêm hôm đó là bao nhiêu?
\( - 7^\circ {\rm{C}}\).
\( - 11^\circ {\rm{C}}\).
\( - 8^\circ {\rm{C}}\).
\( - 10^\circ {\rm{C}}\).
Một chung cư có 25 tầng và 2 tầng hầm. Tầng trệt được đặt là tầng G, các tầng trên (lầu) được đánh số từ thấp đến cao là 1; 2; 3; …; 25 (tầng cao nhất là 25), các tầng hầm được đánh số từ cao xuống thấp là B1; B2. Một thang máy đang ở tầng 10, sau đó đi lên 7 tầng và xuống 20 tầng rồi lại lên 2 tầng. Hỏi cuối cùng thì thang máy dừng lại ở tầng nào?
B1.
B2.
G.
1.
Nhiệt độ đầu tuần tại một trạm nghiên cứu ở Nam Cực là \( - 20\)℃. Sau 6 ngày nhiệt độ tại đây là \( - 38\)℃. Hỏi trung bình mỗi ngày nhiệt độ thay đổi bao nhiêu độ C?
giảm \(9\)℃.
giảm \(3\)℃.
giảm \(6\)℃.
giảm \(18\)℃.
Cho ba số nguyên \(a,\,\,b,\,\,c.\) Kết luận nào sau đây là đúng?
\[a - \left( {b - c} \right) = a + b + c\].
\[a - \left( {b - c} \right) = a - b - c\].
\[a - \left( {b - c} \right) = - a - b - c\].
\[a - \left( {b - c} \right) = a - b + c\].
Cho tích \[\left( { - a} \right).\left( { - b} \right).\left( { - c} \right)\] với \(a,\,\,b,\,\,c\) là các số nguyên. Biểu thức nào sau đây bằng biểu thức đã cho?
\[\left( { - a} \right).\left( { - b} \right).c\].
\[\left( { - a} \right).b.c\].
\[abc\].
\[\left( { - a} \right).b.\left( { - c} \right)\].
Hình nào dưới đây có ba cạnh bằng nhauvà ba góc bằng nhau?
Hình tam giác.
Hình tam giác đều.
Hình thoi.
Hình vuông.
Hình thang, hình bình hành và hình thoi cùng có tính chất nào sau đây?
Hai cạnh đối bằng nhau.
Hai cạnh đối song song.
Bốn cạnh bằng nhau.
Hai đường chéo bằng nhau.
Hình chữ nhật có tính chất nào sau đây?
Các cạnh bằng nhau.
Hai đường chéo vuông góc với nhau.
Bốn góc bằng nhau và bằng 60°.
Hai đường chéo bằng nhau.
Hình thoi có tính chất nào sau đây?
Hai đường chéo bằng nhau.
Bốn góc bằng nhau.
Hai đường chéo vuông góc với nhau.
Cả A, B, C đều đúng.
Hình bình hành không có tính chất nào sau đây?
Các cạnh đối song song với nhau.
Các cạnh đối bằng nhau.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hai đường chéo bằng nhau.
Hình thang cân có tính chất nào dưới đây?
Hai cạnh đối bằng nhau.
Hai đường chéo vuông góc với nhau.
Hai góc kề một cạnh bên bằng nhau.
Hai cạnh bên bằng nhau.
Trong các khẳng định sau, khẳng định nào đúng?
Hình lục giác đều có 5 góc bằng nhau.
Hình thang cân có hai cạnh bên song song với nhau.
Hình vuông có hai đường chéo vuông góc với nhau.
Hình bình hành có bốn cạnh bằng nhau.
Hình thoi có độ dài hai đường chéo lần lượt là \(10{\rm{\;cm}}\) và \(15{\rm{\;cm}}\) có diện tích là
\(25{\rm{\;c}}{{\rm{m}}^2}\).
\(75{\rm{\;c}}{{\rm{m}}^2}\).
\(150{\rm{\;c}}{{\rm{m}}^2}\).
\(300{\rm{\;c}}{{\rm{m}}^2}\).
Hình bình hành có độ dài một cạnh bằng \(3{\rm{\;cm}}\) và diện tích bằng \(18{\rm{\;c}}{{\rm{m}}^2}\) thì chiều cao ứng với cạnh \(3{\rm{\;cm}}\) là
\(3{\rm{\;cm}}\).
\(6{\rm{\;cm}}\).
\(4{\rm{\;cm}}\).
\(9{\rm{\;cm}}\).
Một mảnh vườn hình chữ nhật có chiều rộng \[40{\rm{\;m}}\] và diện tích là \[3\,\,600{\rm{\;}}{{\rm{m}}^2}\]. Chu vi mảnh vườn là
\[130{\rm{\;m}}\].
\[150{\rm{\;m}}\].
\[260{\rm{\;m}}\].
\[250{\rm{\;m}}\].
Hình vuông có diện tích bằng \(100{\rm{\;c}}{{\rm{m}}^2}\) thì có chu vi là
\(20{\rm{\;cm}}\).
\(40{\rm{\;cm}}\).
\(100{\rm{\;cm}}\).
\(200{\rm{\;cm}}\).
Bác Hưng uốn một dây thép thành móc treo đồ có dạng hình thang cân với độ dài hai cạnh đáy và cạnh bên lần lượt là \[30{\rm{\;cm}},\,\,24{\rm{\;cm}}\] và \[5{\rm{\;cm}}\]. Để làm móc treo đó thì bác Hưng cần dây thép có độ dài là bao nhiêu?
\[59{\rm{\;cm}}\].
\[64{\rm{\;cm}}\].
\[68{\rm{\;cm}}\].
\[128{\rm{\;cm}}\].
Hình thang có diện tích bằng bằng \(32{\rm{\;c}}{{\rm{m}}^2}\) và độ dài đường cao là \(8{\rm{\;cm}}\). Biết đáy lớn gấp ba lần đáy nhỏ thì độ dài đáy nhỏ là
\(2{\rm{\;cm}}\).
\(4{\rm{\;cm}}\).
\(6{\rm{\;cm}}\).
\(8{\rm{\;cm}}\).
Hình bình hành có độ dài một cạnh bằng \(10{\rm{\;cm}}\) và chiều cao tương ứng bằng \(5{\rm{\;cm}}\) thì có diện tích gấp mấy lần diện tích hình vuông có cạnh \(5{\rm{\;cm}}?\)
2.
3.
4.
5.
Sân nhà bác Hùng có dạng hình chữ nhật với chiều dài \(6{\rm{\;m}}\) và chiều rộng \(4{\rm{\;m}}\). Bác Hùng mua loại gạch lát nền hình vuông có cạnh \(50{\rm{\;cm}}\) thì cần bao nhiêu viện gạch để đủ lát sân?
\(90\) viên.
\(96\) viên.
\(100\) viên.
\(105\) viên.
Trong các hình sau, hình nào có trục đối xứng?
Hình thoi, hình thang cân, hình chữ nhật.
Hình thoi, hình thang cân, hình bình hành.
Hình thoi, hình chữ nhật, hình bình hành.
Hình thang cân, hình chữ nhật, hình bình hành.
Trong các hình sau, hình nào có tâm đối xứng?
Hình vuông, hình tam giác đều, hình thang cân.
Hình vuông, hình lục giác đều, hình bình hành.
Hình vuông, hình thang cân, hình lục giác đều.
Hình tam giác đều, hình lục giác đều, hình bình hành.
Trong các khẳng định sau, khẳng định nào đúng?
Hình vuông không có trục đối xứng.
Hình tam giác đều có một trục đối xứng.
Hình thang cân có 3 trục đối xứng.
Hình tròn có vô số trục đối xứng.
Cho các chữ cái sau đây:

Có bao nhiêu chữ cái có trục đối xứng?
5.
6.
7.
8.
Trong các hình dưới đây hình nào có tâm đối xứng?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Mỗi hình vẽ dưới đây vẽ những đường nét chính của một công trình kiến trúc biểu tượng nổi tiếng trên thế giới.

Hình nào không có trục đối xứng?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho các biển báo giao thông sau:

Biển nào có tâm đối xứng?
Biển báo số 103a.
Biển báo số P.102.
Biển báo số 127.
Biển báo số P.118.
Cho các hình vẽ sau:

Hình vẽ nào có nhiều hơn 1 trục đối xứng?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho các hình dưới đây:

Có bao nhiêu hình có trục đối xứng?
0.
1.
2.
3.
Cho hình vẽ bên. Nếu vẽ hình đối xứng với hình bên phải của đường thẳng \(d\) qua đường thẳng \(d\) thì ta được một chữ cái. Chữ cái đó là
Chữ W.
Chữ M.
Chữ N.
Chữ V.
2. Trắc nghiệm trả lời đúng/sai.
Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Tế bào lớn lên đến một kích thước nhất định thì phân chia. Quá trình đó diễn ra như sau: Đầu tiên từ 1 nhân thành 2 nhân tách xa nhau. Sau đó chất tế bào được phân chia, xuất hiện một vách ngăn, ngăn đôi tế bào cũ thành 2 tế bào con. Các tế bào con tiếp tục lớn lên cho đến khi bằng tế bào mẹ. Các tế bào này tiếp tục phân chia thành 4, rồi thành 8, … tế bào.
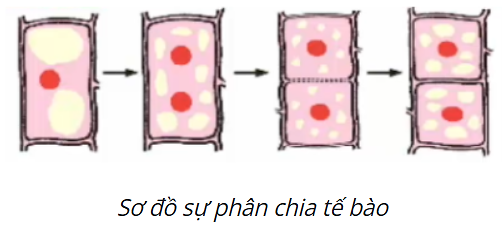
Như vậy từ một tế bào mẹ: sau khi phân chia lần 1 được hai tế bào con; lần hai được \[{2^{2\;}} = 4\] (tế bào con); lần ba được \[{2^3}\; = 8\] (tế bào con). Hãy tính số tế bào con có được ở lần phân chia thứ 5, thứ 8 và thứ 11.
a) Cứ sau mỗi lần phân chia, số tế bào con nhân đôi so với lần trước đó.
b)Số tế bào con có được ở lần phân chia thứ 5 là 32 tế bào con.
c)Số tế bào con có được ở lần phân chia thứ 8 nhiều hơn ở lần thứ 5 là 8 tế bào con.
d) Để tạo ra 1024 tế bào con thì cần đến lần phân bào thứ 9.
Lớp 6A lên kế hoạch tham gia hoạt động làm sạch các khu vực xung quanh trường học. Lớp có 18 bạn nữ và 24 bạn nam. Các bạn muốn chia lớp thành các nhóm nhỏ gồm cả nữ và nam sao cho số bạn nữ và nam chia đều thành các nhóm.
a)Số nhóm chia được là bội của cả 18 và 24.
b)Số nhóm chia được nhiều nhất là ước chung lớn nhất của 18 và 24.
c) Số nhóm chia được nhiều nhất có thể là 6 nhóm.
d)Khi chia thành số nhóm nhiều nhất có thể, mỗi nhóm có 3 bạn nữ.
Cho một mảnh đất hình thang như hình dưới đây. Biết rằng cứ mỗi mét vuông thì trồng được 2 cây hoa và chi phí trồng cây là \(20\,\,000\) đồng/cây.
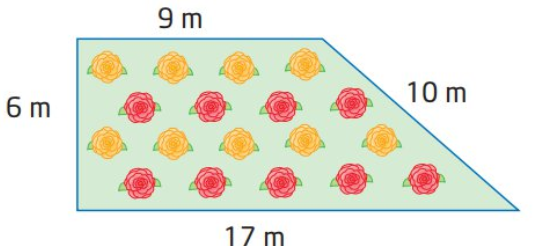
a) Diện tích của mảnh đất hình thang đó là \(78{\rm{ }}{{\rm{m}}^2}{\rm{.}}\)
b) Nếu người ta rào xung quanh mảnh đất bằng dây thép thì cần \({\rm{78 m}}\) dây thép.
c) Trồng được tất cả 156 cây hoa trên mảnh vườn.
d) Chi phí trồng cây cho cả khu vườn lớn hơn 3 triệu đồng.
Một khu vườn hình vuông có chu vi bằng \(48\;{\rm{m}}{\rm{.}}\) Trên mảnh vườn đó, người ta sử dụng \(\frac{1}{6}\) diện tích khu đất để trồng hoa. Biết rằng mỗi mét vuông trồng được 4 cây hoa.
a) Độ dài cạnh hình vuông bằng \(12\;{\rm{m}}{\rm{.}}\)
b)Diện tích của khu vườn đó nhỏ hơn \(100\;{{\rm{m}}^2}.\)
c)Diện tích đất để trồng hoa là \(36\;{{\rm{m}}^2}.\)
d) Số cây hoa cần để trồng trên mảnh đất đó lớn hơn 100 cây.
Cho hình bình hành \(ABCD\) có tâm đối xứng là điểm \(O\) và \(OA = 6\;{\rm{cm,}}\;\,OB = 4\;{\rm{cm}}{\rm{.}}\)
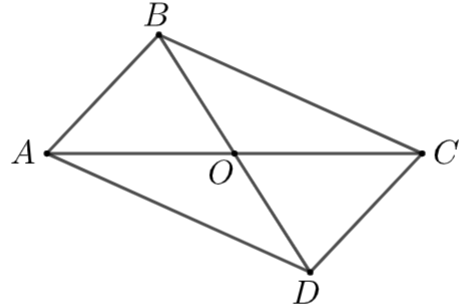
a)\(O\) là giao điểm của hai đường chéo \(AC\) và \(BD.\)
b)\(O\) vừa là trung điểm của \(AC\) vừa là trung điểm của \(BD.\)
c)\(AC = 12\;{\rm{cm}}{\rm{.}}\)
d)Tổng độ dài hai đường chéo của hình bình hành \(ABCD\) bằng \(30\;{\rm{cm}}{\rm{.}}\)
Học sinh của một trường THCS đồng diễn thể dục thể thao. Biết số học sinh của trường khi xếp thành 12 hàng, 18 hàng, 28 hàng đều vừa đủ. Biết rằng số học sinh trong khoảng từ 500 đến 600. Gọi số học sinh trường THCS đó là \(x\) học sinh, khi đó:
a) Điều kiện \(500 \le x \le 600,\,\,x \in {\mathbb{N}^*}.\)
b) Số học sinh của trường THCS đó là \({\rm{BC}}\left( {12,\,\,18,\,\,28} \right)\).
c) \({\rm{BCNN}}\left( {12,\,\,18,\,\,28} \right) = 84\).
d) Trường THCS đó có \(588\) học sinh.
Cho hai số \(28\) và \(42.\) Khi đó ta có:
a) \(6 \in \)ƯC\(\left( {28,\,\,42} \right).\)
b) \(168 \in {\rm{BC}}\left( {28,\,\,42} \right).\)
c) ƯCLN\(\left( {28,\,\,42} \right) = 14.\)
d) \({\rm{BCNN}}\left( {28,\,\,42} \right) = 84.\)
Trong ngày hội “Phụ nữ khởi nghiệp”, một cơ sở mật ong sú vẹt đã chuẩn bị sẵn một số chai mật ong để bày bán trong gian hàng của xã mình. Biết rằng số chai mật ong đó khi xếp bào các thùng mà mỗi thùng 10 chai, 12 chai hay 20 chai đều vừa đủ và số chai trong khoảng từ 150 đến 200 chai. Gọi số chai mật ong mà cơ sở đó đã chuẩn bị là \(x\) (chai).
a) Điều kiện \(150 < x < 200,\,\,x \in {\mathbb{N}^*}.\)
b) \(x \in {\rm{BC}}\left( {10,\,\,12,\,\,20} \right).\)
c) \({\rm{BCNN}}\left( {10,\,\,12,\,\,20} \right) = 60.\)
d) Cơ sở đó đã chuẩn bị 120 chai mật ong.
Bức tường trang trí của một ngôi nhà được xây bằng 40 viên gạch hình vuông có độ dài cạnh là \(25\,\,{\rm{cm}}{\rm{.}}\) Biết rằng một viên gạch có giá \(18\,\,000\)đồng và số tiền chủ nhà đã phải thanh toán là \(1\,\,170\,\,000\) đồng (gồm tiền mua gạch và tiền công thợ). Không tính diện tích của các mạch vữa, khi đó:
a) Diện tích một viên gạch hình vuông bằng \(625{\rm{ }}{{\rm{m}}^2}.\)
b) Diện tích bức tường đó là \(2,5\,\,{{\rm{m}}^2}.\)
c) Số tiền mua gạch là \(720\,\,000\) đồng.
d) Số tiền trả công thợ xây tường lớn hơn số tiền mua gạch.
Cho hình thoi \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O.\)
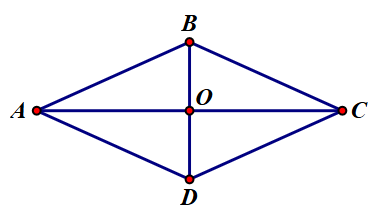
a) Hai đường chéo \(AC\) và \(BD\) vuông góc với nhau.
b) Hình thoi \(ABCD\) có bốn trục đối xứng.
c) Diện tích của hình thoi \(ABCD\) bằng tích độ dài của hai đường chéo \(AC\) và \(BD.\)
d) Các cặp cạnh đối của hình thoi bằng nhau và song song với nhau.
Sau một quý kinh doanh, anh Bình lãi được \(90\) triệu đồng, anh Minh lỗ \(36\) triệu đồng.
a) Sau một quý kinh doanh, số tiền anh Minh thu được là \(36\) triệu đồng.
b) Trung bình một tháng, anh Bình lãi \(30\) triệu đồng.
c)Trung bình một tháng, anh Minh thu được \( - 9\) triệu đồng.
d) Trung bình một tháng, anh Bình thu được nhiều hơn anh Trung \(21\) triệu đồng.
Cho các số \( - 40;\;\,22;\;\,16;\;\, - 31;\;\,18;\;\, - 30;\;\, - 60.\) Khi đó:
a)Các số \( - 40;\;\,22;\;\,16;\;\,18;\;\, - 30;\;\, - 31\) đều chia hết cho 2.
b)Tập hợp \(\left\{ {18;\;\, - 30;\;\, - 60} \right\}\) gồm các số là bội của 3.
c)Có 3 số là bội chung của 2 và 3.
d)Tổng các bội chung của 2 và 3 là một số nguyên âm.
Một tàu ngầm đang ở độ sâu cách mặt biển \(15\;{\rm{m}}{\rm{.}}\) Cứ mỗi phút, tàu lại nổi lên trên \(3\;{\rm{m}}{\rm{.}}\)
a)Ban đầu, tàu ngầm ở độ cao \( - 15\;{\rm{m}}\) so với mặt nước biển.
b) Sau 2 phút, tàu nổi lên trên được \(6\;{\rm{m}}{\rm{.}}\)
c)Tàu ở độ cao \(9\;{\rm{m}}\)so với mực nước biển sau 2 phút.
d) Sau 5 phút, tàu ở mặt nước biển.
3. Trắc nghiệm trả lời ngắn
Hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Một lớp có 45 học sinh, trong đó mỗi học sinh đều giỏi ít nhất một trong hai môn Toán hoặc Văn, biết rằng có 30 học sinh giỏi toán, 25 học sinh giỏi văn. Hỏi lớp đó có bao nhiêu học sinh giỏi cả môn Toán và Văn?
Cho một số có hai chữ số. Nếu viết thêm chữ số 1 vào bên trái và bên phải ta được một số mới gấp 23 lần số đã cho. Tìm số đã cho.
Một tàu hỏa muốn chở 892 học sinh đi tham quan khu di tích Địa Đạo Củ Chi. Biết rằng mỗi xe chở được 45 học sinh. Hỏi nhà trường cần ít nhất bao nhiêu chiếc xe?
Tìm giá trị của \(x \in \mathbb{N},\) biết: \(10 + 2x = {4^5}:{4^3}\).
Học sinh khối lớp 6 của một trường có từ 160 đến 190 học sinh. Khi cho xếp hàng 3 hoặc 4 hoặc 5 đều vừa đủ. Hỏi khối 6 của trường đó có bao nhiêu học sinh?
Một hình thoi có diện tích là \(20\,\,{\rm{c}}{{\rm{m}}^2},\) biết độ dài một đường chéo là \(10\,\,{\rm{cm}}{\rm{.}}\) Tính độ dài đường chéo còn lại. (Đơn vị: cm)
Sân nhà bác An có dạng hình chữ nhật, chiều dài \(12\,\,{\rm{m}}\) và chiều rộng \(9\,\,{\rm{m}}{\rm{.}}\) Bác An mua gạch lát hình vuông có cạnh \(0,6\,\,{\rm{m}}{\rm{.}}\) Hỏi bác An cần mua bao nhiêu viên gạch để lát đủ sân?
Tìm giá trị nguyên của \(x\) thỏa mãn \(5 + {3^{x + 1}} = 86\).
Trong nghi lễ thượng cờ lúc 6 giờ sáng và hạ cờ lúc 21 giờ hàng ngày ở Quảng trường Ba Đình, đội tiêu binh có 34 người một sĩ quan chỉ huy đứng đầu và 33 chiến sĩ. Hỏi có bao nhiêu cách sắp xếp 33 chiến sĩ thành các hàng, sao cho mỗi hàng có số như nhau?
Một thửa ruộng hình thoi có độ dài đường chéo bé bằng \(24{\rm{ m,}}\) độ dài đường chéo lớn gấp 2 lần đường chéo bé. Hỏi diện tích của thửa ruộng đó bằng bao nhiêu? (Đơn vị: m)
Một mũi khoan của một giàn khoan đang ở độ cao \(5\;{\rm{m}}\) so với mực nước biển. Nó được điều khiển đi xuống \(14\;{\rm{m}}\) rồi lại được điều khiển lên \(7\;{\rm{m}}{\rm{.}}\) Hỏi sau hai lần điều khiển mũi khoan, độ cao của mũi khoan so với mực nước biển là bao nhiêu mét?
Nhiệt độ lúc 11 giờ sáng trong 5 ngày liên tiếp ở thành phố A là:
\(3^\circ {\rm{C;}}\;\,2^\circ {\rm{C;}}\;\,{\rm{1}}^\circ {\rm{C;}}\;\, - 4^\circ {\rm{C;}}\;\, - 7^\circ {\rm{C}}{\rm{.}}\)
Nhiệt độ trung bình trong năm ngày đó là bao nhiêu độ C?
Có bao nhiêu số nguyên \(x\) sao cho \(2x - 3\) là bội của \(x + 1.\)



