40 câu hỏi
Tập hợp các căn bậc hai của 25 là
\(\{ 5\} .\)
\(\{ - 5\} .\)
\(\{ - 5;5\} .\)
\(\{ 625\} .\)
Cho \({\rm{a}},{\rm{b}}\) là các số dương khác 1. Phát biểu nào sau đây là đúng?
\(a = {a^{{{\log }_a}b}}.\)
\({\rm{b}} = {{\rm{a}}^{{{\log }_{\rm{a}}}{\rm{b}}}}.\)
\({\rm{b}} = {{\rm{b}}^{{{\log }_a}\;{\rm{b}}}}.\)
\({\rm{a}} = {{\rm{a}}^{{{\log }_b}{\rm{a}}}}.\)
Số 16 có bao nhiêu căn bậc hai?
1.
2.
3.
4.
Cho \({\rm{a}} > 0,{\rm{a}} \ne 1\) và \({\rm{x}},{\rm{y}}\) là hai số dương. Phát biểu nào sau đây là đúng?
\({\log _a}(xy) = {\log _a}x \cdot {\log _a}y.\)
\({\log _a}(xy) = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}.\)
\({\log _{\rm{a}}}({\rm{xy}}) = {\log _{\rm{a}}}{\rm{x}} + {\log _{\rm{a}}}{\rm{y}}.\)
\({\log _a}(xy) = \frac{{{{\log }_a}y}}{{{{\log }_a}x}}.\)
Cho \({\rm{a}} > 0,{\rm{a}} \ne 1\) và x, y là hai số dương. Phát biểu nào sau đây là đúng?
\({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y.\)
\({\log _a}\frac{x}{y} = {\log _a}x \cdot {\log _a}y.\)
\({\log _a}\frac{x}{y} = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}.\)
\({\log _a}\frac{x}{y} = {\log _a}x + {\log _a}y.\)
Cho và Phát biểu nào sau đây là đúng?
\({\log _a}{x^\alpha } = \frac{1}{\alpha }{\log _a}x.\)
\({\log _{\rm{a}}}{{\rm{x}}^\alpha } = {\log _{\rm{a}}}(\alpha {\rm{x}}).\)
\({\log _{\rm{a}}}{{\rm{x}}^\alpha } = {\log _{\rm{a}}}\frac{{\rm{x}}}{\alpha }.\)
\({\log _{\rm{a}}}{{\rm{x}}^\alpha } = \alpha {\log _{\rm{a}}}{\rm{x}}.\)
Cho \({\rm{a}} > 0,{\rm{a}} \ne 1\) và x, y là hai số dương. Phát biểu nào sau đây là đúng?
\({\left( {{{\rm{a}}^{\rm{x}}}} \right)^{\rm{y}}} = {{\rm{a}}^{{\rm{xy}}}}.\)
\({\left( {{a^x}} \right)^y} = {a^{x + y}}.\)
\({\left( {{a^x}} \right)^y} = {a^{x - y}}.\)
\({\left( {{a^x}} \right)^y} = {a^{\frac{x}{y}}}.\)
Cho \({\rm{a}} > 0,{\rm{a}} \ne 1\) và n là số nguyên dương. Phát biểu nào sau đây là đúng?
\({{\rm{a}}^{ - {\rm{n}}}} = - {{\rm{a}}^{\rm{n}}}.\)
\({{\rm{a}}^{ - {\rm{n}}}} = \frac{1}{{{{\rm{a}}^{\rm{n}}}}}.\)
\({{\rm{a}}^{ - {\rm{n}}}} = \frac{{ - 1}}{{{{\rm{a}}^{\rm{n}}}}}.\)
\({a^{ - {\rm{n}}}} = {{\rm{a}}^{\rm{n}}}.\)
Cho \({\rm{a}} > 0,{\rm{a}} \ne 1\) và n là số nguyên dương lớn hơn 1. Phát biểu nào sau đây là đúng?
\(\sqrt[n]{a} = {a^{\frac{1}{n}}}.\)
\(\sqrt[n]{a} = - {a^{\frac{1}{n}}}.\)
\(\sqrt[n]{{\rm{a}}} = \frac{{\rm{a}}}{{\rm{n}}}.\)
\(\sqrt[n]{{\rm{a}}} = \frac{1}{{{{\rm{a}}^{\frac{1}{n}}}}}.\)
Cho \({\rm{a}} = {\log _2}3,\;{\rm{b}} = {\log _5}3.\) Biểu thức \({\log _{10}}3\) bằng
\(\frac{{{\rm{ab}}}}{{{\rm{a}} + {\rm{b}}}}.\)
\(\frac{1}{{\rm{a}}} + \frac{1}{{\;{\rm{b}}}}.\)
\(\frac{1}{{{\rm{ab}}}}.\)
ab.
Phát biểu nào sau đây là đúng?
\({\log _2}{x^2} = 2{\log _2}x,\forall x \ne 0.\)
\({\log _2}{{\rm{x}}^2} = \frac{1}{2}{\log _2}{\rm{x}},\forall {\rm{x}} \ne 0.\)
\({\log _2}{x^2} = {2^2}{\log _2}|x|,\forall x \ne 0.\)
\({\log _2}{x^2} = 2{\log _2}|x|,\forall x \ne 0.\)
Cho a là số dương khác \(1;{\rm{m}},{\rm{n}},{\rm{p}},{\rm{q}}\) là các số nguyên dương lớn hơn 1. Phát biểu nào sau đây là đúng?
\({\log _{\sqrt[m]{{{a^a}}}}}\sqrt[p]{{{a^q}}} = \frac{m}{n} \cdot \frac{q}{p}.\)
\({\log _{\sqrt[m]{{{a^n}}}}}\sqrt[p]{{{a^q}}} = \frac{n}{m} \cdot \frac{q}{p}.\)
\({\log _{\sqrt[m]{{{a^a}}}}}\sqrt[p]{{{a^q}}} = \frac{m}{n} \cdot \frac{p}{q}.\)
\({\log _{\sqrt[m]{{{a^n}}}}}\sqrt[p]{{{a^q}}} = \frac{n}{m} \cdot \frac{p}{q}.\)
Cho \({\rm{a}},{\rm{b}}\) là hai số thực dương thoả mãn \({{\rm{a}}^2} + {{\rm{b}}^2} = 98{\rm{ab}}.\) Phát biểu nào sau đây là đúng?
\(2{\log _2}({\rm{a}} + {\rm{b}}) = {\log _2}{\rm{a}} + {\log _2}\;{\rm{b}}.\)
\({\log _2}\frac{{a + b}}{2} = {\log _2}a + {\log _2}b.\)
\(2{\log _2}\frac{{a + b}}{{10}} = {\log _2}a + {\log _2}\;{\rm{b}}.\)
\({\log _2}\frac{{a + b}}{{10}} = 2\left( {{{\log }_2}a + {{\log }_2}b} \right)\)
Biết \({\log _2}3 = {\rm{a}}\) và \({\log _2}5 = {\rm{b}}.\) Kết quả tính \({\log _5}360\) theo a và b là
\(\frac{{3{\rm{a}} + {\rm{b}} + 2}}{{\;{\rm{b}}}}.\)
\(\frac{{2{\rm{a}} + {\rm{b}} + 3}}{{\;{\rm{b}}}}.\)
\({\rm{b}}(2{\rm{a}} + {\rm{b}} + 3).\)
\({\rm{b}}(3{\rm{a}} + {\rm{b}} + 2).\)
Biết \({\log _8}3 = {\rm{a}}\) và \({\log _3}5 = {\rm{b}}.\) Kết quả tính \({\log _{10}}3\) theo a và b là
\(3{\rm{a}} + {\rm{b}}.\)
ab.
\(\frac{1}{{a + 3b}}.\)
\(\frac{{3{\rm{a}}}}{{1 + 3{\rm{ab}}}}.\)
Biết \({\rm{a}} = {\log _2}3\) và \({\rm{b}} = {\log _2}5.\) Giá trị của biểu thức \({\log _{15}}45\) bằng
\(\frac{{{\rm{a}} + {\rm{b}}}}{{2{\rm{a}} + {\rm{b}}}}.\)
\(\frac{{a + 2b}}{{a + b}}.\)
\(\frac{{2a + b}}{{a + b}}.\)
\(\frac{{a + b}}{{a + 2b}}.\)
Tập xác định của hàm số \(y = {x^{\frac{1}{7}}}\) là
\(\mathbb{R}\backslash 0.\)
\(\mathbb{R}.\)
\((0; + \infty ).\)
\([0; + \infty ).\)
Tập xác định của hàm số \({\rm{y}} = {{\rm{x}}^7}\) là
\(\mathbb{R}\backslash 0.\)
\(\mathbb{R}.\)
\((0; + \infty ).\)
\([0; + \infty ).\)
Tập xác định của hàm số \({\rm{y}} = {{\rm{x}}^{ - 7}}\) là
\(\mathbb{R}\backslash 0.\)
\(\mathbb{R}.\)
\((0; + \infty ).\)
\([0; + \infty ).\)
Tập xác định của hàm số \({\rm{y}} = {7^{\rm{x}}}\) là
\(\mathbb{R}\backslash 0.\)
\(\mathbb{R}.\)
\((0; + \infty ).\)
\([0; + \infty ).\)
Tập xác định của hàm số \({\rm{y}} = {\log _7}{\rm{x}}\) là
\(\mathbb{R}\backslash 0.\)
\(\mathbb{R}.\)
\((0; + \infty ).\)
\([0; + \infty ).\)
Đạo hàm của hàm số \(y = {x^7}\) là
\(7{x^6}.\)
\(\frac{{{x^8}}}{8}.\)
\({x^6}.\)
\({x^8}.\)
Đạo hàm của hàm số \({\rm{y}} = {7^{\rm{x}}}\) là
\({7^x}\ln 7.\)
\({7^{{\rm{x}} - 1}}.\)
\(\frac{{{7^x}}}{{\ln 7}}.\)
\(({\rm{x}} - 1) \cdot {7^{{\rm{x}} - 1}}.\)
Đạo hàm của hàm số \({\log _7}x\) là
\(\frac{1}{{\rm{x}}}.\)
\(\frac{1}{{{\rm{x}}\log 7}}.\)
\(\frac{{\ln 7}}{x}.\)
\(\frac{1}{{x\ln 7}}.\)
Đạo hàm của hàm số \({\log _7}(1 - x)\) là
\(\frac{1}{{x - 1}}.\)
\(\frac{1}{{(x - 1)\log 7}}.\)
\(\frac{1}{{(x - 1)\ln 7}}.\)
\(\frac{1}{{(1 - x)\ln 7}}.\)
Hình bên là đồ thị hàm số nào?
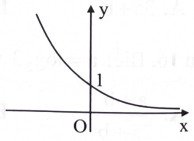
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\({\rm{y}} = {\log _{\rm{a}}}{\rm{x}},0 < {\rm{a}} < 1.\)
Hình bên là đồ thị hàm số nào?
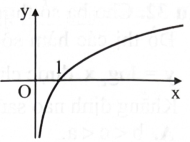
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\({\rm{y}} = {\log _a}{\rm{x}},0 < {\rm{a}} < 1.\)
Hình bên là đồ thị hàm số nào?
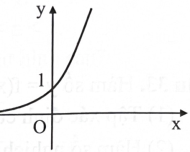
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\({\rm{y}} = {\log _a}{\rm{x}},0 < {\rm{a}} < 1.\)
Hình bên là đồ thị hàm số nào?
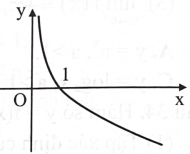
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\({\rm{y}} = {\log _a}{\rm{x}},0 < {\rm{a}} < 1.\)
Trong các hàm số sau đây, hàm số nào có đồ thị phù hợp với hình bên?
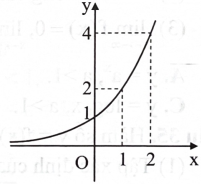
\({\rm{y}} = {{\rm{e}}^{\rm{x}}}.\)
\({\rm{y}} = {2^{\rm{x}}}.\)
\({\rm{y}} = {2^{ - {\rm{x}}}}.\)
\(y = {e^{ - x}}.\)
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \({\rm{y}} = {\log _{\rm{a}}}{\rm{x}},{\rm{y}} = {\log _{\rm{b}}}{\rm{x}}\), \({\rm{y}} = {\log _{\rm{c}}}{\rm{x}}\) được cho như hình vẽ bên. Khẳng định nào sau đây là đúng?
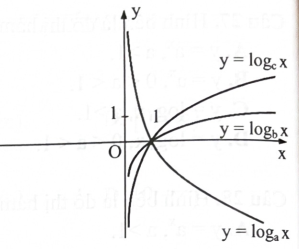
\({\rm{b}} < {\rm{c}} < {\rm{a}}.\)
\({\rm{c}} < {\rm{a}} < {\rm{b}}.\)
\({\rm{a}} < {\rm{c}} < {\rm{b}}.\)
\({\rm{a}} < {\rm{b}} < {\rm{c}}.\)
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \((0; + \infty ).\)
(2) Hàm số nghịch biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = + \infty ,\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty .\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \(\mathbb{R}.\)
(2) Hàm số đồng biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 0,\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty .\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{y}} = {{\rm{b}}^{\rm{x}}},{\rm{y}} = {{\rm{c}}^{\rm{x}}}\) được cho như hình vẽ bên. Khẳng định nào sau đây là đúng?
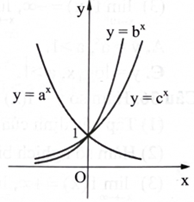
\({\rm{b}} < {\rm{c}} < {\rm{a}}.\)
\({\rm{a}} < {\rm{c}} < {\rm{b}}.\)
\({\rm{c}} < {\rm{a}} < {\rm{b}}.\)
\({\rm{a}} < {\rm{b}} < {\rm{c}}.\)
Hàm số \(y = f(x)\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \((0; + \infty ).\)
(2) Hàm số đồng biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = - \infty ,\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty .\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \(\mathbb{R}.\)
(2) Hàm số nghịch biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty ,\mathop {\lim }\limits_{x \to + \infty } f(x) = 0.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có bảng biến thiên như hình sau?
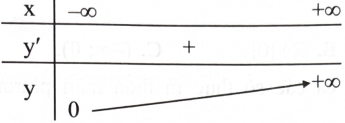
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Hàm số y=f(x) nào sau đây có bảng biến thiên như hình sau?
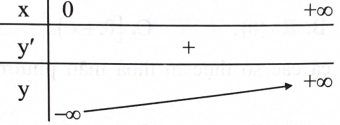
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Hàm số y=f(x) nào sau đây có bảng biến thiên như hình sau?
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Hàm số y=f(x) nào sau đây có bảng biến thiên như hình sau?
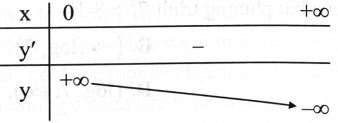
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
\(y = {\log _a}x,a > 1.\)
\(y = {\log _a}x,0 < a < 1.\)
Gợi ý cho bạn
Xem tất cảCÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
CÂU TRẮC NGHIỆM ĐÚNG SAI
DẠNG 4. BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT PHƯƠNG TRÌNH LÔGARIT