CÂU TRẮC NGHIỆM ĐÚNG SAI

b) Hàm số đã cho có giá trị nhỏ nhất là -1 và giá trị lớn nhất là 1.

c) Hàm số đã cho đồng biến trên \(\left( {\frac{{ - \pi }}{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\forall k \in \mathbb{Z}\) và nghịch biến trên \(\left( {\frac{\pi }{2} + {\rm{k}}2\pi ;\frac{{3\pi }}{2} + {\rm{k}}2\pi } \right)\forall {\rm{k}} \in \mathbb{Z}.\)

d) Trên đoạn \([ - \pi ;\pi ]\), hàm số đã cho có bảng biến thiên như bảng sau:

a) Hàm số đã cho là hàm lẻ.

b) Hàm số đã cho có giá trị nhỏ nhất là -1 và giá trị lớn nhất là 1.

c) Hàm số đã cho đồng biến trên \((k2\pi ;\pi  + k2\pi )\forall k \in \mathbb{Z}\) và nghịch biến trên \((\pi  + {\rm{k}}2\pi ;2\pi  + {\rm{k}}2\pi )\forall {\rm{k}} \in \mathbb{Z}.\)

d) Trên đoạn \(\left[ {\frac{{ - \pi }}{2};\frac{{3\pi }}{2}} \right]\), hàm số đã cho có bảng biến thiên như bảng sau:

a) Hàm số đã cho là hàm lẻ.

b) Hàm số đã cho có giá trị nhỏ nhất là -1 và giá trị lớn nhất là 1.

c) Hàm số đã cho đồng biến trên \(\left( {\frac{{ - \pi }}{2} + {\rm{k}}\pi ;\frac{\pi }{2} + {\rm{k}}\pi } \right)\forall {\rm{k}} \in \mathbb{Z}.\)

d) Trên khoảng \(\left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\), hàm số đã cho có bảng biến thiên như bảng sau:

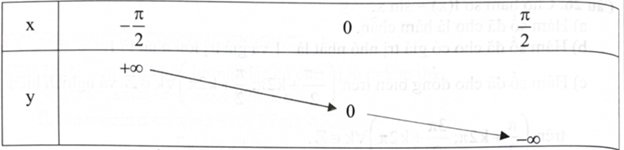
a) Hàm số đã cho là hàm chẵn.

b) Hàm số đã cho có giá trị nhỏ nhất là -1 và giá trị lớn nhất là 1.

c) Hàm số đã cho nghịch biến trên \(({\rm{k}}\pi ;\pi  + {\rm{k}}\pi )\forall {\rm{k}} \in \mathbb{Z}.\)

d) Trên khoảng \((0;\pi )\), hàm số đã cho có bảng biến thiên như bảng sau:

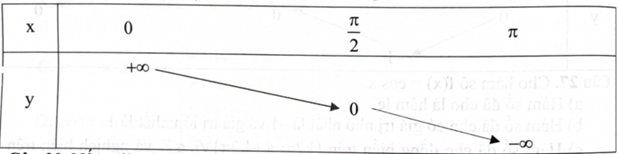
a) \(\cos 3x = - \sin \left( {\frac{\pi }{2} - 3x} \right)\)

b) \(\sin x = \cos 3x \Leftrightarrow \sin x =  - \sin \left( {\frac{\pi }{2} - 3x} \right)\)

c) \(\sin x = \cos 3x \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} - 3x + k2\pi }\\{x = \pi - \left( {\frac{\pi }{2} - 3x} \right) + k2\pi }\end{array},k \in \mathbb{Z}} \right..\)

d) Phương trình \(\sin x = \cos 3x\) có nghiệm là \(x = \frac{\pi }{8} + \frac{{k\pi }}{2},x = \frac{{ - \pi }}{4} + k\pi ,k \in \mathbb{Z}.\)