Bộ 5 đề thi giữa kì 2 Toán 11 Cánh diều cấu trúc mới (Đề số 4)
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mẫu số liệu sau cho biết cân nặng của học sinh lớp 12 trong một lớp

Số học sinh của lớp đó là bao nhiêu?
\(37\).
\(35\).
\(33\).
\(31\).
Hai bạn Triết và Khang, mỗi người gieo đồng thời một con xúc xắc cân đối, đồng chất. Xét hai biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc bạn Triết gieo là số lẻ”.
B: “Số chấm xuất hiện trên con xúc xắc bạn Khang gieo là số chia hết cho 5”.
Chọn câu đúng:
Hai biến cố A, B là hai biến cố độc lập.
Hai biến cố A, B là hai biến cố xung khắc.
Biến cố A giao B là \(\left\{ {1;3;5} \right\}\).
Biến cố A hợp B là \(\left\{ {1;2;3;5} \right\}\).
Với \(a\) là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
\({a^{\frac{5}{2}}}\).
\(a\).
\({a^{\frac{3}{2}}}\).
\({a^{\frac{1}{4}}}\).
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
\(\frac{5}{{2a}}\).
\(\frac{{5a}}{2}\).
\(\frac{2}{{5a}}\).
\(\frac{{2a}}{5}\).
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{e}} \right)^x}\).
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\).
\(y = {\left( {\frac{1}{3}} \right)^x}\).
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\).
Cho \({\log _a}b = 2\) với \(a,b\) là số thực dương và \(a\) khác 1. Tính giá trị biểu thức \(T = {\log _{{a^2}}}{b^6} + {\log _a}\sqrt b \).
\(T = 7\).
\(T = 6\).
\(T = 5\).
\(T = 8\).
Trong hình vẽ bên có đồ thị các hàm số \(y = {a^x},y = {b^x},y = {\log _c}x\). Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
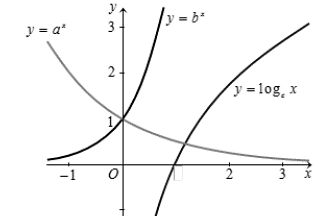
\(a < c < b\).
\(c < a < b\).
\(a < b = c\).
\(b < c < a\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Góc giữa hai đường thẳng \(SD\) và \(BC\) bằng
Góc giữa hai đường thẳng \(SD\) và \(DC\).
Góc giữa hai đường thẳng \(SD\) và \(AD\).
Góc giữa hai đường thẳng \(SD\) và \(BD\).
Góc giữa hai đường thẳng \(SD\) và \(SC\).
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình vuông tâm \(O\). Hình chiếu của điểm \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là điểm
\(B\).
\(D\).
\(O\).
\(A\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) đều cạnh \(a\) và \(SA = a\) (tham khảo hình vẽ). Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng
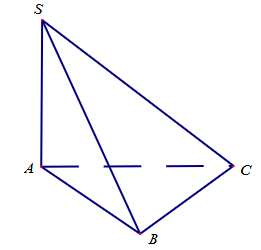
\(45^\circ \).
\(60^\circ \).
\(135^\circ \).
\(90^\circ \).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\) và các cạnh bên bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm \(AD\) và \(SD\). Số đo góc \(\left( {MN,SC} \right)\) bằng
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.

Tính mốt của mẫu số liệu ghép nhóm này (làm tròn đến hàng phần trăm).
\(153,18\).
\(153,81\).
\(154,18\).
\(153,28\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Gọi \(A\) là biến cố “Rút được tấm thẻ ghi số chẵn lớn hơn 9”; \(B\) là biến cố “Rút được tấm thẻ ghi số từ 9 đến 14”.
a) \(A\) và \(B\) là hai biến cố xung khắc.
b) \(P\left( A \right) = \frac{3}{{10}}\).
c) \(P\left( {AB} \right) = \frac{1}{5}\).
d) \(P\left( {A \cup B} \right) = \frac{9}{{20}}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có \(AB = a,BC = 2a\) và \(SA \bot \left( {ABCD} \right)\), cạnh \(SA = a\sqrt {15} \).
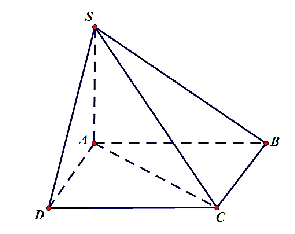
a) \(AC \bot SA\).
b) \(BD \bot \left( {SAC} \right)\).
c) \(BC \bot SB\).
d) Góc tạo bởi đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(30^\circ \).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 15 đến câu 18.
Cho \(a > 0,a \ne 1\). Tính giá trị của biểu thức \(M = {\log _a}\left( {{a^3}} \right) - 2{\log _a}\left( {\frac{1}{a}} \right) + 2{\log _a}\sqrt a \).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy, \(SA = a\). Gọi \(M\) là trung điểm cạnh \(SB\). Góc giữa hai đường thẳng \(AM\) và \(BD\) bằng bao nhiêu độ?
Trong vật lí, sự phân rã các chất phóng xạ được cho bởi công thức \(m\left( t \right) = {m_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\). Trong đó, \({m_0}\) là khối lượng chất phóng xạ ban đầu (tại thời điểm \(t = 0\)), \(m\left( t \right)\) là khối lượng chất phóng xạ tại thời điểm \(t\) và \(T\) là chu kì bán rã. Hạt nhân Poloni (\({P_0}\)) là chất phóng xạ \(\alpha \)có chu kì bán rã 138 ngày. Giả sử lúc đầu có 100 Poloni. Tính khối lượng Poloni còn lại sau 100 ngày theo đơn vị gam (làm tròn kết quả đến phần chục).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Gọi \(H\) là trung điểm của \(AB\) và \(SH \bot \left( {ABCD} \right)\), gọi \(K\) là trung điểm của cạnh \(AD\). Góc giữa hai đường thẳng \(BK\) và \(SC\) bằng bao nhiêu độ?
PHẦN II. TỰ LUẬN
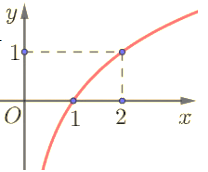
Cho các hàm số \(y = {\log _2}x;y = {\log _{\frac{1}{2}}}x;y = {\left( {\frac{1}{2}} \right)^x}\) và \(y = {2^x}\). Đồ thị hàm số dưới đây là của hàm số nào đã cho?
Một tổ học sinh có 12 bạn, trong đó có 6 bạn thích môn Bóng đá, 4 bạn thích môn Cầu lông và 2 bạn thích cả hai môn Bóng đá và Cầu lông. Chọn ngẫu nhiên một học sinh trong tổ. Tính xác suất để chọn được bạn đó không thích cả môn Bóng đá và Cầu lông.
Một ngôi nhà có hai mái trước, sau có dạng là các hình chữ nhật \(ABCD,ABMN\) và \(AD = 4\;{\rm{m}}\), \(AN = 3\;{\rm{m}}\), \(DN = 5\;{\rm{m}}\)(hình vẽ minh hoạ). Tính góc nhị diện tạo bởi hai nửa mặt phẳng chứa hai mái nhà đó.