Bộ 3 đề thi giữa kì 1 Vật lý 11 Chân trời sáng tạo có đáp án - Đề 3
30 câu hỏi
Dao động là chuyển động có
giới hạn trong không gian lặp đi lặp lại nhiều lần quanh một vị trí cân bằng.
qua lại hai bên vị trí cân bằng và không giới hạn không gian.
trạng thái chuyển động được lặp lại như cũ sau những khoảng thời gian bằng nhau.
lặp đi lặp lại nhiều lần có giới hạn trong không gian.
Phát biểu nào sau đây đúng
Dao động tuần hoàn là dao động điều hòa
Dao động điều hòa là dao động có li độ biến thiên theo thời gian được biểu thị bằng quy luật dạng sin (hay cosin).
Đồ thị biểu diễn li độ của dao động tuần hoàn biến thiên theo thời gian luôn là một đường hình sin.
Biên độ của dao động điều hòa thì không thay đổi theo thời gian, còn biên độ của dao động tuần hoàn thì thay đổi theo thời gian.
Một chất điểm dao động điều hòa với phương trình x = Acos(ωt + φ), trong đó A, ω là các hằng số dương. Pha của dao động ở thời điểm t là
ωt + φ.
ω.
φ.
ωt.
Một vật dao động điều hòa trên trục Ox quanh vị trí cân bằng O. Gọi A, ω và φ lần lượt là biên độ, tần số góc và pha ban đầu của dao động. Biểu thức li độ của vật theo thời gian t là
\[x = A\cos \left( {\omega t + \varphi } \right).\]
\[x = \omega A\cos \left( {t\varphi + A} \right).\]
\[x = t\cos \left( {\omega A + \varphi } \right).\]
\[x = \varphi \cos \left( {\omega A + t} \right).\]
Trong phương trình dao động điều hòa x = Acos(ωt + φ), đại lượng (ωt + φ) được gọi là
biên độ dao động.
tần số của dao động.
pha của dao động.
chu kì của dao động.
Một chất điểm dao động theo phương trình x = 6cos(πt + π/2) cm. Dao động của chất điểm có chiều dài quỹ đạo là
6 cm.
3 cm.
12 cm.
24 cm.
Vật dao động điều hoà trên quỹ đạo dài 6 cm, biên độ dao động là:
12 cm.
3 cm.
6 cm.
1,5 cm.
Một vật dao động điều hòa theo phương trình x = 5cos(8πt + π/2) cm. Tần số góc của dao động là
8π rad/s.
4 rad/s.
8 rad/s.
4π rad/s.
Một vật dao động điều hoà, trong thời gian một phút vật thực hiện 30 dao động. Chu kì dao động của vật là
1 s.
30 s.
2 s.
0,5 s.
Một vật dao động điều hòa cứ sau mỗi phút vật qua vị trí cân bằng được 180 lần. Tần số góc của dao động là
\[\frac{{2\pi }}{3}\] rad/s.
π rad/s.
2π rad/s.
3π rad/s.
Cho hai dao động điều hòa cùng tần số x1 = 2cos(πt + 4π/3) (cm) và x2 = 3sin(πt + π/3) (cm). Nhận xét nào dưới đây là đúng ?
hai dao động ngược pha nhau.
dao động thứ nhất có pha ban đầu là 4π/3.
dao động thứ hai có pha ban đầu là π/3.
hai dao động vuông pha với nhau.
Một chất điểm dao động điều hòa với phương trình li độ \[x = 2\cos \left( {2\pi t + \frac{\pi }{2}} \right)\] (x tính bằng cm, t tính bằng s). Tại thời điểm \[t = \frac{1}{4}s\], chất điểm có li độ bằng
2 cm.
\[\sqrt 3 \]cm
\[ - \sqrt 3 \] cm
– 2 cm.
Điểm M dao động điều hoà theo phương trình: \[x = \frac{5}{2}\sin \left( {\pi t + \frac{\pi }{4}} \right)\left( {cm} \right)\]
Vào thời điểm nào thì pha dao động đạt giá trị \[\frac{\pi }{3}\] rad, lúc ấy li độ x bằng bao nhiêu?
t = 1/60 s, x = 0,72 cm.
t = 1/6 s, x = 1,4 cm.
t = 1/12 s, x = 2,16 cm.
t = 1/12 s, x = 1,25 cm.
Một chất điểm dao động điều hòa với phương trình x = 6cos(πt) (x tính bằng cm, t tính bằng s). Tốc độ lớn nhất của chất điểm trong quá trình dao động là:
3π cm/s.
6π cm/s.
2π cm/s.
π cm/s.
Một chất điểm dao động điều hòa với gia tốc cực đại là amax = 0,2π2 m/s2 và vận tốc cực đại là vmax = 10π cm/s. Biên độ và chu kỳ của dao động của chất điểm lần lượt là
A = 500 cm và T = 2 (s).
A = 5 cm và T = 1 (s).
A = 0,05 m và T = 0,2π (s).
A = 500 cm và T = 2π (s).
Con lắc lò xo dao động điều hòa với biên độ \[A = 10\]cm. Khi đi qua li độ \[x = 5\] cm thì vật có động năng bằng \[0,3\]J. Độ cứng của lò xo là
100 N/m.
80 N/m.
50 N/m.
40 N/m.
Cơ năng đàn hồi của hệ vật và lò xo
bằng động năng của vật.
bằng tổng động năng của vật và thế năng đàn hồi của lò xo.
bằng thế năng đàn hồi của lò xo.
bằng động năng của vật và cũng bằng thế năng đàn hồi của lò xo.
Cho một vật nặng M, khối lượng m = 1 kg treo vào một lò xo thẳng đứng có độ cứng k = 400 N/m. Gọi Ox là trục tọa độ có phương trùng với phương dao động của M, và có chiều hướng lên trên, điểm gốc O trùng với vị trí cân bằng. Khi M dao động tự do với biên độ 5 cm, tính động năng Wd1 và Wd2 của quả cầu khi nó đi ngang qua vị trí x1 = 3 cm và x2 = –3 cm.
Wd1 = 0,18 J và Wd2 = – 0,18 J.
Wd1 = 0,18 J và Wd2 = 0,18 J.
Wd1 = 0,32 J và Wd2 = – 0,32 J.
Wd1 = 0,32 J và Wd2 = 0,32 J.
Hai con lắc đơn cùng khối lượng, dao động điều hòa tại cùng một nơi, với cùng biên độ góc và với chu kỳ lần lượt là T1 = 2 s, T2 = 1 s. Tỉ số cơ năng toàn phần \[\frac{{{W_1}}}{{{W_2}}}\] của hai con lắc này là
0,5.
2.
4.
0,25.
Hai con lắc đơn dao động điều hoà tại một nơi trên Trái Đất, có năng lượng như nhau. Quả nặng của chúng có cùng khối lượng. Chiều dài dây treo con lắc thứ nhất dài gấp bốn lần chiều dài dây treo con lắc thứ hai (ℓ = 4ℓ2). Quan hệ giữa các biên độ góc của hai con lắc là
α1 = 4α2.
α1 = 2α2.
α1 = α2/2.
α1 = α2/4.
Đồ thị dao động điều hoà của một vật như hình vẽ.
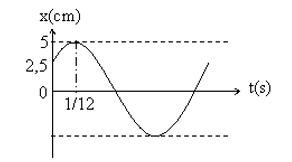
Phương trình dao động của vật là:
x = 5cos(2πt – π/3)(cm).
x = 5cos(4πt – π/3)(cm).
x = 5cos(2πt + π/6)(cm).
x = 5cos(4πt + π/3)(cm).
Một chất điểm dao động điều hòa trên trục Ox. Đồ thị biểu diễn li độ, vận tốc, gia tốc theo thời gian có dạng như hình bên. Đường (1), (2) và (3) lần lượt biểu diễn
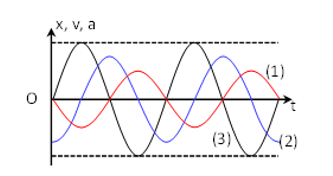
v, x.
v, x, a.
x, v, a.
x, a, v.
Hai dao động x1 và x2 có đồ thị theo hình vẽ.
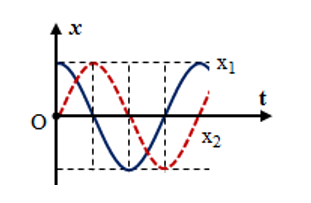
Hãy cho biết hai dao động đó lệch pha nhau như thế nào?
x1 và x2 lệch pha nhau π/4.
x1 và x2 lệch pha nhau π/2.
x1 và x2 ngược pha.
x1 và x2 cùng pha.
Một con lắc lò xo dao động điều hòa. Nếu tăng độ cứng của lò xo lên 2 lần và giảm khối lượng của vật 2 lần thì chu kì dao động của con lắc sẽ
tăng 2 lần.
không thay đổi.
tăng 4 lần.
giảm 2 lần.
Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều hòa. Nếu khối lượng m = 200 g thì chu kỳ dao động của con lắc là 2 s. Để chu kỳ con lắc là 1 s thì khối lượng m bằng
200 g.
800 g.
50 g.
100 g.
Một con lắc lò xo gồm vật nặng có khối lượng 40 g, độ cứng lò xo 5 N/m được kích thích dao động điều hòa. Chu kì dao động của con lắc là
2,22 s.
0,14 s.
1,78 s.
0,56 s.
Một con lắc lò xo gồm lò xo có khối lượng không đáng kể, có độ cứng k = 100 N/m, khối lượng của vật nặng m = 1 kg. Kéo vật khỏi vị trí cân bằng x = 3 cm và truyền cho vật vận tốc v = 30 cm/s theo chiều dương. Chọn t = 0 là lúc vật bắt đầu chuyển động. Phương trình dao động của vật là
\[x = 3\sqrt 2 \cos \left( {10t + \frac{\pi }{4}} \right)cm\].
\[x = 3\sqrt 2 \cos \left( {10t + \frac{\pi }{3}} \right)cm\].
\[x = 3\sqrt 2 \cos \left( {10t + \frac{{3\pi }}{4}} \right)cm\].
\[x = 3\sqrt 2 \cos \left( {10t - \frac{\pi }{4}} \right)cm\].
Chọn phát biểu sai?
Dao động điều hòa là dao động mà li độ được mô tả bằng một định luật dạng sin (hoặc cosin) theo thời gian: x = Acos(ωt + φ) trong đó A, ω , φ là những hằng số.
Dao động điều hòa có thể được coi là hình chiếu của chuyển động tròn đều xuống đường thẳng nằm trong mặt phẳng quỹ đạo.
Dao động điều hòa có thể được biểu diễn bằng một vectơ không đổi.
Khi một vật dao động điều hòa thì vận tốc của vật đó cũng biến thiên điều hòa.
Một chất điểm chuyển động tròn đều trên đường tròn tâm O với tốc độ dài là 30 cm/s, có gia tốc hướng tâm là 1,5 m/s2 thì hình chiếu của nó trên đường kính quỹ đạo dao động điều hòa với biên độ
6 cm.
4,5 cm.
5 cm.
7,5 cm.
Cho một chất điểm đang dao động điều hòa. Pha ban đầu của dao động bằng
π (rad) nếu tại thời điểm ban đầu (t = 0) chất điểm đi qua vị trí cân bằng theo chiều dương.
π/2 (rad) nếu tại thời điểm ban đầu (t = 0) chất điểm đi qua vị trí cân bằng theo chiều âm.
0 (rad) nếu tại thời điểm ban đầu (t = 0) chất điểm đi qua vị trí biên về phía âm.
π/2 (rad) nếu tại thời điểm ban đầu (t = 0) chất điểm đi qua vị trí biên về phía dương.








