12 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn
(Thí sinh trả lời từ Câu 1 đến Câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án)
Biểu thức nào sau đây không phải là phân thức đại số?
\(\frac{{3x}}{y}.\)
\(\frac{{x - 2}}{0}.\)
\(\frac{1}{2}x + 1.\)
\(\frac{3}{{x + 4}}.\)
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
\[0x + 3 = 0.\]
\[{x^2} - 2 = 0.\]
\(\frac{1}{2}x - 3 = 0.\)
\(\frac{5}{x} + 1 = 0.\)
Đồ thị của hai hàm số \(y = 2025x + 1\) và \(y = 2026x + 1\) là hai đường thẳng có vị trí như thế nào?
Trùng nhau.
Song song.
Không cắt nhau.
Cắt nhau.
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\[2{x^2} + \;2 = \;0.\]
\[3y - 1 = \;5\left( {y - \;2} \right).\]
\(2x + \frac{y}{2} = 1.\)
\(3\sqrt x + {y^2} = 0.\)
Cho hình chóp tứ giác đều \[S.ABCD\] (hình bên), \[SH\] được gọi là
![Cho hình chóp tứ giác đều \[S.ABCD\] (hình bên), \[SH\] được gọi là (ảnh 1)](https://video.vietjack.com/upload2/images/1755653258/1755653342-image1.png)
đường cao.
cạnh bên.
cạnh đáy.
đường chéo
Cho \(\Delta ABC\) vuông tại \(A\) có \(AC = 4\,\,{\rm{cm}},\,\,AB = 3\,\,\,{\rm{cm}}.\) Khi đó \[\tan B\] bằng
\(\frac{3}{4}\).
\(\frac{3}{5}\).
\(\frac{4}{5}\).
\(\frac{4}{3}\).
Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 2” là
Thẻ ghi số 2 và thẻ ghi số 3.
Thẻ ghi số 2 và thẻ ghi số 4.
Thẻ ghi số 2 và thẻ ghi số 5.
Thẻ ghi số 3 và thẻ ghi số 4.
Cho tam giác \[ABC\] đồng dạng với tam giác \[MNP\] theo tỉ số 2. Khẳng định nào sau đây là đúng?
\[MN = 2AB.\]
\[AC = 2NP.\]
\[MP = 2BC.\]
\[BC = 2NP.\]
Cặp số \[\left( { - 2\,;\,\, - 3} \right)\] là nghiệm của hệ phương trình nào sau đây?
\[\left\{ \begin{array}{l}x - 2y = 3\\2x + y = 4\end{array} \right..\]
\[\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 8\end{array} \right..\]
\[\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 7\end{array} \right..\]
\[\left\{ \begin{array}{l}4x - 2y = 0\\x - 3y = 5\end{array} \right..\]
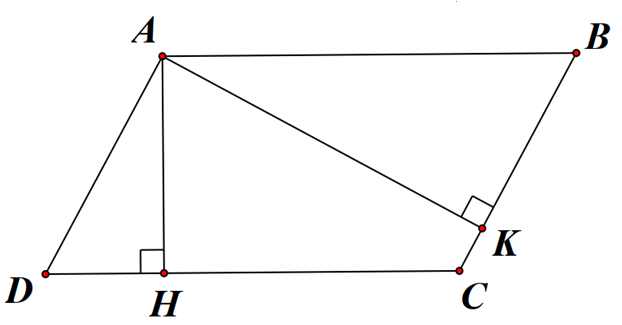
Cho hình bình hành \[ABCD,\] kẻ \[AH \bot CD\] tại \[H,\] \[AK \bot BC\] tại \[K.\] Khẳng định nào sau đây là đúng?
Bạn An gieo một con xúc xắc 50 lần và thống kê lại kết quả các lần gieo ở bảng sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
8 |
9 |
9 |
5 |
6 |
13 |
Xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ” sau 50 lần thử trên là
\[0,46.\]
\[0,52.\]
\[0,54.\]
\[0,48.\]
Cho \[\Delta ABC\] vuông tại \[A,\] đường cao \[AH\] có \[AC = 15\,\,{\rm{cm}},\,\,CH = 6\,\,{\rm{cm}}.\] Tỉ số lượng giác \(\cos B\) bằng
\[\frac{5}{{\sqrt {21} }}.\]
\[\frac{{\sqrt {21} }}{5}.\]
\[\frac{5}{2}.\]
\[\frac{2}{5}.\]
