12 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Cho biểu đồ thống kê tỉ lệ phần trăm điểm khá giỏi môn Toán mỗi tổ so với cả lớp, những tổ có điểm khá giỏi bằng nhau là
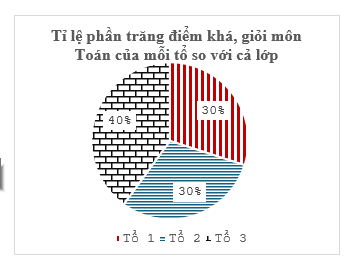
Tổ 1 và tổ 2.
Tổ 2 và tổ 3.
Tổ 3 và tổ 1.
Tổ 1, tổ 2 và tổ 3.
Rút ngẫu nhiên một quả bóng bán từ một chiếc hộp đựng 9 quả bóng có đánh số: \(0;1;2;3;\)\(4;5;6;7;8;9\). Biến cố “Rút được quả bóng có ghi số 9” là biến cố gì?
Biến cố chắc chắn.
Biến cố ngẫu nhiên.
Biến cố không thể.
Biến cố đã xảy ra.
Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá \(10{\rm{ 000}}\) đồng là
\(10000x.\)
\(10000 + x.\)
\(\frac{{10000}}{x}.\)
\(\frac{x}{{10000}}.\)
Biểu thức đại số biểu thị tổng của hai số tự nhiên lẻ liên tiếp là
\(x - \left( {x + 2} \right)\) với \(x = 2k + 1,k \in \mathbb{N}.\)
\(x + \left( {x + 2} \right)\) với \(x = 2k + 1,k \in \mathbb{N}.\)
\(x + \left( {x + 1} \right)\) với \(x = 2k + 1,k \in \mathbb{N}.\)
\(x - \left( {x + 1} \right)\) với \(x = 2k + 1,k \in \mathbb{N}.\)
Bậc của đa thức \(11{x^{10}} + x + 5{x^3} - 3{x^4} - 11{x^{10}} - 3{x^5} - 6\) là
\(3.\)
\(4.\)
\(5.\)
\(9.\)
Kết quả của phép tính \(\frac{1}{6}{x^3}.{\left( { - 2x} \right)^2}\) là
\( - \frac{2}{3}{x^5}.\)
\(\frac{2}{3}{x^5}.\)
\( - \frac{2}{3}{x^6}.\)
\(\frac{2}{3}{x^6}.\)
Cho tam giác \(ABC\) có \(\widehat B\) là góc tù và \(\widehat A > \widehat C\). Khẳng định nào sau đây là đúng?
\(AC > AB > BC.\)
\(BC > AB > AC.\)
\(AB > AC > BC.\)
\(AC > BC > AB.\)
Cho \(\Delta ABC\), chọn khẳng định đúng trong các khẳng định sau:
\(AB - AC < BC < AB + AC.\)
\(AB - AC > BC > AB + AC.\)
\(AB - AC < BC < AB.AC.\)
\(AC - AB = BC < AB + AC.\)
Để chứng minh được \(\Delta ABC = \Delta EGH\) theo trường hợp cạnh – góc – cạnh khi đã biết \(AB = EG,\) \(BC = GE\) thì cần chứng minh yếu tố nào?
\(\widehat {ABC} = \widehat {EGH}\).
\(\widehat {ABC} = \widehat {GHE}.\)
\(AC = FE.\)
\(BC = FE.\)
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat A = 100^\circ \). Số đo góc \(B\) là
\(60^\circ .\)
\(30^\circ .\)
\(40^\circ .\)
\(80^\circ .\)
Cho \(I\) là giao điểm của ba đường phân giác trong của một tam giác. Kết luận nào sau đây là đúng?
\(I\) cách đều ba cạnh của tam giác.
\(I\) cách đều ba đỉnh của tam giác.
\(I\) là trọng tâm của tam giác.
\(I\) cách đỉnh một khoảng bằng \(\frac{2}{3}\) độ dài đường phân giác.
Bạn Bình đã lấy một miếng bìa hình tam giác và đặt đầu nhọn của chiếc bút chì vào điểm \(H\) trên hình tam giác thì mấy miếng bìa cân bằng trên đầu bút. Hỏi bạn Bình đã xác định vị trí điểm \(H\) bằng cách nào?
Bạn Bình vẽ hai đường trung trực cắt nhau tại \(H.\)
Bạn Bình vẽ hai đường cao cắt nhau tại \(H.\)
Bạn Bình vẽ hai đường trung tuyến cắt nhau tại \(H.\)
Bạn Bình vẽ hai đường phân giác cắt nhau tại \(H.\)
