12 câu hỏi
Mẫu thức của phân thức \(\frac{{{x^2}\left( {x + 1} \right)}}{{\left( {x - y} \right){y^2}}}\) là
\({x^2}\left( {x + 1} \right)\).
\(\left( {x - y} \right)\).
\(\left( {x - y} \right){y^2}\).
\({y^2}\).
Điều kiện xác định của phân thức \(\frac{{{x^2} - 1}}{{{x^2} - 2x + 1}}\) là
\(x = 1\).
\(x = 1;x = - 1\).
\(x \ne 1;x \ne - 1\).
\(x \ne 1\).
Giả sử các biểu thức đều có nghĩa. Áp dụng quy tắc đổi dấu ta viết được phân thức \(\frac{{5 - x}}{{11 - {x^2}y}}\) bằng phân thức
\(\frac{{5 - x}}{{11 + {x^2}y}}\).
\(\frac{{x - 5}}{{ - 11 + {x^2}y}}\).
\(\frac{{x + 5}}{{11 - {x^2}y}}\).
\(\frac{{x + 5}}{{11 + {x^2}y}}\).
Kết quả của biểu thức \(\frac{3}{{2x + 6}} - \frac{{x - 6}}{{2{x^2} + 6x}}\) là
\(\frac{1}{{x + 3}}.\)
\( - \frac{1}{{x + 3}}\).
\( - \frac{1}{x}.\)
\(\frac{1}{x}\).
Công thức nào dưới đây thể hiện phép nhân hai phân thức \(\frac{A}{B}\) với phân thức \(\frac{M}{N}\)?
\(\frac{A}{B}.\frac{M}{N} = \frac{{A + M}}{{B.N}}\).
\(\frac{A}{B}.\frac{M}{N} = \frac{{A.N}}{{B.M}}\).
\(\frac{A}{B}.\frac{M}{N} = \frac{{A.M}}{{B.N}}\).
\(\frac{A}{B}.\frac{M}{N} = \frac{{A.M}}{{B + N}}\).
Kết quả của phép tính \(\frac{{\left( { - 20x} \right)}}{{3{y^2}}}:\frac{{\left( { - 4{x^3}} \right)}}{{5y}}\) là
\(\frac{{80{x^3}}}{{15{y^3}}}\).
\(\frac{{25x}}{{3y}}\).
\(\frac{{25xy}}{{3{x^2}y}}\).
\(\frac{{25}}{{3{x^2}y}}\).
Đưa phương trình \(5x - \left( {6 - x} \right) = 12\) về dạng \(ax + b = 0\) ta được
\(4x + 6 = 0.\)
\(4x - 18 = 0\).
\(5x - 6 = 0\).
\(6x - 18 = 0\).
Giá trị \(x = - 4\) là nghiệm của phương trình nào dưới đây?
\( - \frac{5}{2}x + 1 = 11\).
\( - \frac{5}{2}x = - 10\).
\(3x - 8 = 0\).
\(3x - 1 = x + 7\).
Cho theo tỉ số \(k\). Vậy \(k\) bằng tỉ số nào dưới đây?
\(k = \frac{{AB}}{{BC}}\).
\(k = \frac{{AC}}{{DF}}\).
\(k = \frac{{DE}}{{AB}}.\)
\(k = \frac{{DE}}{{DF}}\).
Cho \(\Delta DEF\) vuông tại \(E\). Áp dụng định lí Pythagore vào tam giác trên ta được:
\(D{E^2} + E{F^2} = D{F^2}\).
\(D{F^2} + F{E^2} = D{E^2}\).
\(D{E^2} + D{F^2} = E{F^2}\).
\(E{F^2} - D{E^2} = D{F^2}\).
Cho \(\Delta ABC\) và \(\Delta DMN\) như hình vẽ dưới đây:
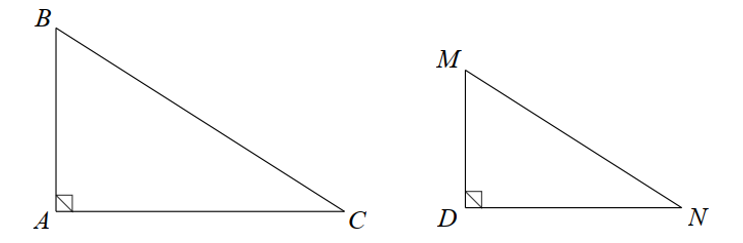
Để (cạnh huyền – cạnh góc vuông) thì cần thêm yếu tố nào dưới đây?
\(\frac{{AB}}{{DM}} = \frac{{AC}}{{DN}}\).
\(\frac{{BC}}{{AC}} = \frac{{MN}}{{DN}}\).
\(\widehat B = \widehat M\).
Cả ba đáp án trên đều đúng.
Trong các cặp hình sau, hình nào là hình đồng dạng?
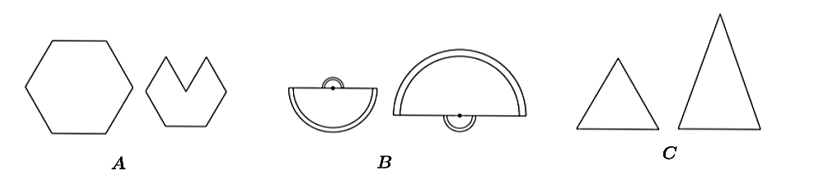
Hình \(A\).
Hình \(B.\)
Hình \(C\).
Không có hình nào.
