12 câu hỏi
Từ đẳng thức \(2.15 = 6.5\) ta lập được tỉ lệ thức nào sau đây?
\(\frac{2}{{15}} = \frac{6}{5}.\)
\(\frac{2}{5} = \frac{{15}}{6}.\)
\(\frac{{15}}{2} = \frac{5}{6}.\)
\(\frac{{15}}{6} = \frac{5}{2}.\)
Nếu có dãy tỉ số bằng nhau \(\frac{a}{x} = \frac{b}{y} = \frac{c}{z}\) thì điều nào sau đây là đúng?
\(a:x = b:y = c:z.\)
\(a:z = b:y = c:x.\)
\(a:b = y:x = c:z.\)
\(a:y = b:x = c:z.\)
Cho bảng số liệu sau:

Chọn khẳng định đúng trong các khẳng định sau:
\(x\) tỉ lệ thuận với \(y\) theo hệ số \(k = 5.\)
\(x\) tỉ lệ nghịch với \(y\) theo hệ số \(a = 5.\)
\(y\) tỉ lệ thuận với \(x\) theo hệ số \(k = 5.\)
\(y\) tỉ lệ nghịch với \(x\) theo hệ số \(a = 5.\)
Biết rằng \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch với nhau. Khi \(x = - \frac{1}{2}\) và \(y = 8\) thì hệ số tỉ lệ \(a\) lúc này là
\(a = 4.\)
\(a = - 16.\)
\(a = - 4.\)
\(a = 16.\)
Trong các biểu thức sau, biểu thức đại số nào chỉ chứa một biến?
\(3x + 3y - 1.\)
\(x + 3y - z.\)
\({z^2} + 3z - 2.\)
\(3{y^2} - y - z.\)
Biểu thức đại số biểu thị tổng của hai số tự nhiên liên tiếp là
\(x + y\) với \(x,y \in \mathbb{N}.\)
\(x + y + 1\) với \(x,y \in \mathbb{N}.\)
\(x + \left( {x + 1} \right)\) với \(x \in \mathbb{N}.\)
\(x + \left( {x + 2} \right)\) với \(x \in \mathbb{N}.\)
Trong các đa thức sau, đa thức nào là đa thức một biến?
\(x + 2y.\)
\({x^2} + 2x + 1.\)
\(xy + 4x.\)
\({x^2} - 4{z^2} + y.\)
Đa thức một biến bậc \(6\) có hai hạng tử mà hệ số cao nhất là \(5\), hệ số tự do là \( - 1\). Đó là đa thức
\(6{x^5} + 1.\)
\(6{x^5} - 1.\)
\(5{x^6} + 1.\)
\(5{x^6} - 1.\)
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\widehat B = 50^\circ \). Khẳng định nào sau đây là đúng?
\(AC < AB.\)
\(BC < AB.\)
\(AC > AB.\)
\(BC < AC.\)
Cho hình vẽ sau:
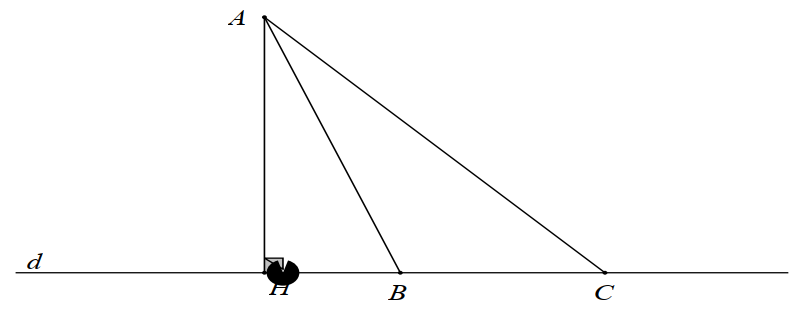
Đường vuông góc kẻ từ điểm \(A\) đến đường thẳng \(d\) là
\(AH.\)
\(AC.\)
\(AB.\)
\(BC.\)
Cho \(\Delta ABC\) có \(BC = 1{\rm{ cm, }}AC = 5{\rm{ cm}}{\rm{.}}\) Nếu \(AB\) có độ dài là một số nguyên thì \(AB\) có số đo là
\(3{\rm{ cm}}{\rm{.}}\)
\({\rm{5 cm}}{\rm{.}}\)
\({\rm{4 cm}}{\rm{.}}\)
\({\rm{6 cm}}{\rm{.}}\)
Cho \(G\) là trọng tâm của \(\Delta DEF\), vẽ đường trung tuyến \(DH.\) Trong các khẳng định sau, khẳng định nào đúng?
\(\frac{{DG}}{{DH}} = \frac{1}{2}.\)
\(\frac{{DG}}{{GH}} = 3.\)
\(\frac{{GH}}{{DH}} = \frac{1}{3}.\)
\(\frac{{GH}}{{DG}} = \frac{2}{3}.\)
