12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số 
. Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của 
trên 
.
A. 
.
A. 
.
C. 
.
D. 
.
Mệnh đề nào dưới đây đúng?
A.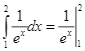 
.
B.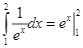 
.
C.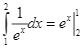 
.
D.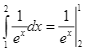 
.
Cho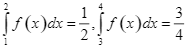 
. Kết quả 
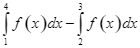bằng
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số 
liên tục trên 
. Gọi 
là diện tích hình phẳng giới hạn bởi đồ thị 
, trục hoành, hai đường thẳng 
(tham khảo hình vẽ bên dưới).
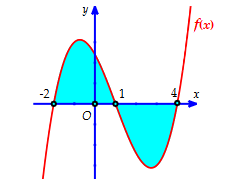
Giả sử 
là diện tích hình phẳng . Mệnh đề nào dưới đây sai?
A.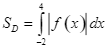 
.
B.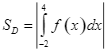 
.
C.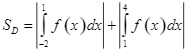 
.
D.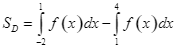 
.
Tính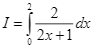 
.
A. 
.
B. 
.
C. 
.
D. 
.
Cho vật thể 
được giới hạn bởi hai mặt phẳng 
. Biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục 
tại điểm có hoành độ 
(
) là một hình vuông có cạnh bằng 
. Thể tích vật thể bằng.
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
cho mặt phẳng 
có một vectơ pháp tuyến là
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, mặt phẳng 
không đi qua điểm nào dưới đây:
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, phương trình mặt phẳng 
đi qua điểm 
và có vectơ pháp tuyến 
là
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, vectơ nào sau đây là một vectơ pháp tuyến của 
, biết 
là cặp vectơ chỉ phương của ?
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, cho mặt phẳng 
. Khoảng cách từ điểm 
đến mặt phẳng 
bằng
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, cho điểm 
và mặt phẳng 
. Mặt phẳng 
đi qua 
và song song với mặt phẳng 
có phương trình:
A. 
.
B. 
.
C. 
.
D. 
.