Bài tập ôn tập Toán 7 Kết nối tri thức Chương 1 có đáp án
55 câu hỏi
A. Trắc nghiệm
Dạng 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Tập hợp các số hữu tỉ được kí hiệu là ?
\(\mathbb{N}.\)
\(\mathbb{Q}.\)
\(\mathbb{Z}.\)
\(\mathbb{R}.\)
Số nào dưới đây không là số hữu tỉ?
\[\frac{3}{0}\].
\[2.\]
\[0,5.\]
\[4\frac{5}{7}\].
Khẳng định nào sau đây là sai?
\(5 \in \mathbb{Q}.\)
\(\frac{{ - 5}}{7} \in \mathbb{Q}.\)
\(\frac{4}{3}\not \in \mathbb{Q}.\)
\( - 3 \in \mathbb{Q}.\)
Cặp số hữu tỉ nào dưới đây bằng nhau?
\(\frac{{ - 12}}{8}\) và \(\frac{3}{{ - 2}}\).
\(\frac{{10}}{{11}}\) và \(\frac{9}{{10}}.\)
\(\frac{6}{8}\) và \(\frac{{12}}{{15}}.\)
\(\frac{5}{7}\) và \(\frac{7}{5}.\)
Số hữu tỉ \( - 0,6\) được biểu diễn ở dạng phân số là
\(\frac{{ - 3}}{5}.\)
\(\frac{3}{5}.\)
\(\frac{{ - 3}}{{ - 5}}.\)
\(\frac{6}{{10}}.\)
Cho trục số.

Điểm \(B\) trên trục số biểu diễn số hữu tỉ nào?
\(\frac{7}{5}\).
\(\frac{{ - 2}}{5}\).
\(\frac{9}{5}\).
\(\frac{3}{5}\).
Điền dấu thích hợp vào chỗ chấm \(3,25.... - 3\frac{4}{7}\) là
\( \le \).
=.
<.
>.
Trong các số \[ - \frac{{ - 15}}{8};\,\,\frac{{ - 20}}{{ - 45}};\,\,10,35;\,\, - 3\frac{5}{2};\,\,\frac{0}{7};\,\,\frac{{2023}}{{2024}}\] có bao nhiêu số hữu tỉ dương?
1.
2.
3.
4.
Đối với biểu thức có chứa dấu ngoặc thì thứ tự thực hiện phép tính trên tập số hữu tỉ nào dưới đây là đúng?
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\).
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}\).
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right)\).
\(\left( {} \right) \to \left\{ {} \right\} \to \left[ {} \right]\).
Các số \( - 2,15\,;\,\,\frac{5}{4};\,\, - 3\frac{1}{5};\,\,2\,;\,\,0\) được sắp xếp theo thứ tự giảm dần là
\[2;\,\,\frac{5}{4};\,\,0;\,\, - 2,15;\,\, - 3\frac{1}{5}\].
\[0;\,\,\frac{5}{4};\,\,2;\,\, - 2,15;\,\, - 3\frac{1}{5}\].
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,\frac{5}{4};\,\,2\).
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,2;\,\,\frac{5}{4}\).
Khi bỏ dấu ngoặc trong biểu thức \[ - \left( { - a + b - 5 - c} \right)\] ta được kết quả là
\[ - a + b - 5 - c.\]
\[a + b - 5 - c.\]
\[a - b + 5 + c.\]
\[ - a - b + 5 + c.\]
Khẳng định nào dưới đây là đúng?
\[\frac{5}{3} > \frac{{ - 3}}{4}.\]
\[\frac{4}{7} > \frac{4}{3}.\]
\[\frac{{ - 4}}{9} > \frac{{ - 4}}{{11}}.\]
\[\frac{{ - 11}}{9} > \frac{{ - 4}}{5}.\]
Tổng \[\frac{{ - 4}}{3} - \frac{2}{7} + \frac{2}{{ - 3}} + \frac{2}{7}\] bằng
\[ - 2.\]
0.
\[ - 1.\]
4.
Kết quả của phép tính \[\frac{2}{3} + \frac{4}{5}\] là
\[\frac{{22}}{{15}}.\]
\[\frac{6}{8}.\]
\[\frac{6}{{15}}.\]
\[\frac{8}{{15}}.\]
Kết quả của phép tính \(\frac{3}{4} + \frac{1}{4} \cdot \left( {\frac{{ - 12}}{{20}}} \right)\) bằng
\(\frac{{ - 12}}{{20}}.\)
\(\frac{3}{5}.\)
\(\frac{{ - 3}}{5}.\)
\(\frac{{ - 9}}{{84}}.\)
Kết quả của phép tính \({\left( { - \frac{2}{5}} \right)^2}\) là
\( - \frac{4}{{25}}.\)
\( - \frac{2}{5}.\)
\(\frac{4}{{25}}.\)
\(\frac{4}{{10}}.\)
Chọn khẳng định sai trong các khẳng định sau:
\[{\left( { - 2019} \right)^0} = 1.\]
\[\left( {0,5} \right) \cdot {\left( {0,5} \right)^2} = \frac{1}{4}.\]
\[{4^6}:{4^4} = 16\].
\[{\left( { - 3} \right)^3} \cdot {\left( { - 3} \right)^2} = {\left( { - 3} \right)^5}.\]
Kết quả của phép chia \[{\left( {\frac{2}{3}} \right)^7}:{\left( {\frac{2}{3}} \right)^5}\] là
\[\frac{{{2^2}}}{3}.\]
\[{\left( {\frac{2}{3}} \right)^2}.\]
\[\frac{2}{3}.\]
\[\frac{2}{{{3^2}}}.\]
Tập tất cả các giá trị của \[x\] để \[{x^2} = 49\] là
\[\left\{ 7 \right\}.\]
\[\left\{ { - 7} \right\}.\]
\[\emptyset .\]
\[\left\{ { - 7;7} \right\}.\]
Giá trị của thỏa mãn \[{\left( {x - \frac{1}{3}} \right)^3} = \frac{{ - 1}}{{27}}\] là
\[\frac{8}{{27}}\].
\[\frac{2}{3}\].
\[0\].
\[0\]và \[\frac{2}{3}\].
Cho \[{20^n}:{5^n} = 4.\] Giá trị của \[n\] là
\[n = 0.\]
\[n = 3.\]
\[n = 2.\]
\[n = 1.\]
Trong số những khẳng định sau, khẳng định nào sai?
\[{x^m} \cdot {x^n} = {x^{m + n}}.\]
\[{x^0} = 1.\]
\[{x^1} = 1.\]
\[\frac{{{x^m}}}{{{x^n}}} = {x^{m - n}}\,\,\left( {x \ne 0;\,\,m \ge n} \right).\]
Giá trị của phép tính \({2^x} = {\left( {{2^2}} \right)^2}\) là
5.
4.
\({2^4}.\)
2.
Chu vi tam giác có độ dài ba cạnh bằng \[\frac{{13}}{4}\,\,{\rm{cm;}}\,\,\frac{{11}}{3}\,\,{\rm{cm;}}\,\,\frac{9}{2}\,\,{\rm{cm}}\] là
\[\frac{{33}}{9}{\rm{ cm}}{\rm{.}}\]
\[\frac{{33}}{{12}}{\rm{ cm}}{\rm{.}}\]
\[\frac{{137}}{{12}}{\rm{ cm}}{\rm{.}}\]
\[\frac{{135}}{{12}}{\rm{ cm}}{\rm{.}}\]
Ba xe ô tô cùng chuyển long nhãn từ Hưng Yên lên Hà Nội. Ô tô thứ nhất, thứ hai, thứ ba chuyển được lần lượt \[\frac{1}{3};\,\,\frac{3}{{10}};\,\,\frac{4}{{15}}\] số long nhãn trong kho. Hỏi cả ba ô tô chuyển được bao nhiêu phần long nhãn trong kho?
\[\frac{8}{{10}}.\]
\[\frac{9}{{10}}.\]
\[\frac{7}{{10}}.\]
\[\frac{6}{{10}}.\]
Để làm một cái bánh, cần \(2\frac{2}{3}\) cốc bột. Hằng đã có \(\frac{2}{3}\) cốc bột. Hỏi Hằng cần thêm bao nhiêu cốc bột nữa để vừa đủ làm được một cái bánh?
\(\frac{1}{3}\).
2.
\(\frac{2}{3}\).
\(1\frac{1}{3}\).
Để hoàn thành một công việc, anh Nam cần 10 giờ, anh Việt cần 15 giờ. Nếu hai anh cùng làm trong 1 giờ thì cả hai người làm được số phần công việc là
\(\frac{1}{8}.\)
\(\frac{1}{6}.\)
\(\frac{1}{{30}}.\)
\(\frac{3}{8}.\)
Một xưởng may trong tuần thứ nhất thực hiện được \(\frac{2}{7}\) kế hoạch tháng, tuần thứ hai thực hiện được \(\frac{5}{{14}}\) kế hoạch, trong tuần thứ ba thực hiện được \(\frac{1}{3}\) kế hoạch. Để hoàn thành kế hoạch của tháng thì trong tuần cuối xưởng phải thực hiện được bao nhiêu phần kế hoạch?
\(\frac{1}{{42}}.\)
\(\frac{{41}}{{42}}.\)
\(\frac{{11}}{{41}}.\)
\(\frac{3}{{42}}.\)
Hai mảnh vườn có dạng hình vuông. Mảnh thứ nhất có độ dài cạnh là \(19,5{\rm{ m}}{\rm{.}}\) Mảnh thứ hai có độ dài cạnh là \(6,5{\rm{ m}}{\rm{.}}\) Diện tích mảnh vườn thứ nhất gấp bao nhiêu lần diện tích mảnh vườn thứ hai?
10.
9.
8.
7.
Một hình chữ nhật có chu vi là \(30,6\,{\rm{ cm,}}\) chiều rộng là \(5,5{\rm{ cm}}{\rm{.}}\) Diện tích của hình chữ nhật đó là
\(53,9\,{\rm{ c}}{{\rm{m}}^2}.\)
\(25,1\,{\rm{ c}}{{\rm{m}}^2}.\)
\(138,05\,{\rm{ c}}{{\rm{m}}^2}.\)
\(60,8\,{\rm{ c}}{{\rm{m}}^2}.\)
Giá trị của \(x\) thỏa mãn: \(\left( {\frac{3}{8} - x} \right) - x = \frac{9}{8}\) là
\(\frac{{ - 3}}{8}.\)
\(\frac{{ - 3}}{2}.\)
\(\frac{3}{2}.\)
\(\frac{3}{8}.\)
Giá trị của \(x\) thỏa mãn: \(\frac{2}{3}x - \frac{3}{4}\left( {2x - \frac{{20}}{{21}}} \right) = - 4\frac{2}{7}\) là
\(\frac{{25}}{6}\).
6.
\( - 6.\)
\( - \frac{{25}}{6}\).
Giá trị của biểu thức \(B = \frac{1}{{2022}} \cdot \frac{{ - 6}}{7} + \frac{{2021}}{{2022}} \cdot \frac{{ - 6}}{7} + \frac{6}{7}\) là
\(\frac{6}{7}\).
\(\frac{{ - 6}}{7}\).
0.
1.
Có bao nhiêu giá trị nguyên của \(a\) thỏa mãn \(\frac{a}{{18}}\) là số hữu tỉ lớn hơn \(\frac{{ - 5}}{6}\) và nhỏ hơn \(\frac{{ - 1}}{2}\)?
3.
4.
5.
6.
Giá trị của \(H = \frac{1}{{1 \cdot 2}} + \frac{1}{{2 \cdot 3}} + \frac{1}{{3 \cdot 4}} + ... + \frac{1}{{2017 \cdot 2018}}\) là
\(H = \frac{{2016}}{{2017}}.\)
\(H = \frac{{2017}}{{2018}}.\)
\(H = \frac{{2018}}{{2019}}.\)
\(H = \frac{{2019}}{{2018}}.\)
Dạng 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho trục số sau:
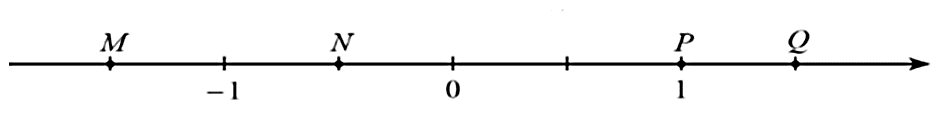
a) Điểm \(Q\) biểu diễn giá trị lớn hơn 1.
b) Khoảng cách từ \(P\) đến \(Q\) là \(\frac{1}{2}\).
c) Chỉ có điểm \(M\) biểu diễn giá trị nhỏ hơn 0.
d) Khoảng cách giữa hai điểm \(M\) và \(N\) bằng khoảng cách giữa hai điểm \(P\) và \(Q.\)
Hai vòi cùng chảy vào một bể. Nếu vòi thứ nhất chảy một mình thì mất 4 giờ 30 phút thì đầy bể. Nếu vòi thứ hai chảy một mình thì mất 6 giờ 45 phút mới đầy bể. Coi toàn bộ bể nước là 1 đơn vị.
a) Trong một giờ, vòi thứ nhất chảy được \(\frac{2}{9}\) bể.
b) Trong một giờ, vòi thứ hai chảy được \(\frac{4}{{27}}\) bể.
c) Trong một giờ, cả hai vòi cùng chảy được một lượng ít hơn \(\frac{1}{3}\) bể.
d) Hai vòi cùng chảy thì sau \(3,5\) giờ sẽ chảy đầy bể.
Bình đọc một cuốn sách trong 4 ngày. Ngày thứ nhất đọc được \(\frac{1}{5}\) cuốn sách, ngày thứ hai đọc được \(\frac{1}{3}\) cuốn sách, ngày thứ ba đọc được \(\frac{1}{4}\) cuốn sách.
a) Ba ngày đầu Bình đọc được \(\frac{{47}}{{60}}\) cuốn sách.
b) Ngày thứ tư Bình đọc được \(\frac{{13}}{{60}}\) cuốn sách.
c) Ngày thứ tư bạn Bình đọc được nhiều nhất trong bốn ngày.
d) Hai ngày đầu bạn Bình đọc được nhiều hơn hai ngày sau.
Người thứ nhất đi xe đạp từ \(A\) đến \(B\) hết \(6\) giờ; người thứ hai đi xe máy từ \(B\) về \(A\) hết \(3\) giờ; người thứ hai khởi hành sau người thứ nhất \(2\) giờ.
a) Sau một giờ người thứ hai đi được \(\frac{1}{3}\) quãng đường.
b) Sau một giờ người thứ nhất đi được \(\frac{1}{6}\) quãng đường.
c) Hai người đã đi được \(\frac{2}{3}\) quãng đường.
d) Sau khi người thứ hai đi được 1 giờ thì hai người gặp nhau.
Lớp 7A tổng kết cuối năm xếp loại học sinh được các danh hiệu: xuất sắc, giỏi, khá (không có học sinh trung bình, yếu, kém). Số học sinh khá chiếm \(\frac{9}{{16}}\) số học sinh cả lớp. Số học sinh giỏi bằng \(\frac{{11}}{{10}}\) số học sinh xuất sắc. Biết rằng lớp 7A có \(48\) học sinh.
a) Số học sinh xuất sắc và giỏi chiếm \(\frac{7}{{16}}\) số học sinh cả lớp.
b) Lớp 7A có \(27\) học sinh khá.
c) Số học sinh xuất sắc và giỏi là \(21\) học sinh.
d) Lớp 7A có 11 học sinh xuất sắc.
Dạng 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x,\) biết: \( - \frac{5}{4}x - \frac{3}{5} = - \frac{{11}}{{10}}.\) (Kết quả ghi dưới dạng số thập phân)
Một kho hàng chứa \(32,8\) tấn gạo. Ngày thứ nhất kho xuất đi \(\frac{3}{4}\) số gạo trong kho, ngày thứ hai kho xuất tiếp \(\frac{3}{4}\) số gạo còn lại, ngày thứ ba kho nhập vào \(3,5\) tấn gạo. Hỏi sau ba ngày trong kho còn lại bao nhiêu kg gạo?
Tính giá trị của \(x\), biết: \(\frac{2}{3}x + \frac{7}{{10}} = \frac{3}{{10}}\).(Kết quả ghi dưới dạng số thập phân)
Tìm giá trị của \(x,\) biết: \(x - \frac{5}{4} = - \frac{1}{2}\).(Kết quả ghi dưới dạng số thập phân)
Bố của Phúc chuẩn bị đi công tác bằng máy bay. Theo kế hoạch, máy bay sẽ cất cánh lúc 10 giờ 30 phút. Bố của Phúc cần phải có mặt ở sân bay trước ít nhất 2 giờ để làm thủ tục, biết rằng đi từ nhà Phúc đến sân bay mất khoảng 45 phút. Hỏi bố của Phúc phải đi từ nhà muộn nhất là lúc mấy giờ đến đến sân bay cho kịp giờ bay? (Kết quả viết dưới dạng số thập phân)
Hai đoạn ống nước có chiều dài lần lượt là \(0,8{\rm{ m}}\) và \(1,35{\rm{ m}}\). Người ta nối hai đầu ống để tạo thành một ống nước mới. Chiều dài của phần nối chung là \(\frac{2}{{25}}{\rm{ m}}{\rm{.}}\) Hỏi đoạn ống nước mới dài bao nhiêu mét? (Kết quả viết dưới dạng số thập phân)
Nhân dịp khai trương, cửa hàng thời trang bán giảm giá tất cả các mặt hàng \(20\% \). Bạn Hạnh dự định mua 2 cái áo giá 200 nghìn đồng/cái và 3 cái quần giá 300 nghìn đồng/cái (đây là giá quần và giá áo khi chưa giảm). Hỏi bạn Hạnh phải trả cho cửa hàng bao nhiêu tiền? (Đơn vị: nghìn đồng)
Lớp 7A cuối năm chỉ có 3 loại học sinh là: giỏi, khá, trung bình (không có học sinh yếu, kém). Số học sinh trung bình chiếm \(\frac{7}{{15}}\) số học sinh cả lớp. Số học sinh khá bằng 140% số học sinh giỏi. Hỏi lớp 7A có bao nhiêu học sinh giỏi, biết rằng lớp 7A có 45 học sinh?
Hưởng ứng phong trào kế hoạch nhỏ của liên Đội, lớp 7A thu được \(102,6{\rm{ kg}}\) giấy vụn. Số giấy vụn lớp 7B thu được bằng \(\frac{2}{3}\) số giấy vụn của lớp 7A. Hỏi lớp 7A thu được nhiều hơn lớp 7B bao nhiêu kilogram giấy vụn?
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\frac{{ - 3}}{2} < \frac{x}{5} < \frac{1}{4}\)?
B. Tự luậnCô Phương kinh doanh hoa quả nhập khẩu. Trong lần nhập hàng vừa qua, cô đã bỏ ra 80 triệu đồng để nhập lô hàng mới. Do quá trình vận chuyển không đảm bảo nên \(\frac{1}{4}\) số hàng nhập về không đảm bảo chất lượng. Cô Phương đã bán số hàng không đảm bảo chất lượng đảm bảo chất lượng đó thấp hơn 15% giá nhập vào còn số lượng hàng còn lại cao hơn \[30\% \] so với giá nhập vào. Hỏi cả lô hàng mới của cô Phương lãi bao nhiêu tiền?
Nhân dịp khai trương chi nhánh mới, cửa hàng giảm giá \[10\% \] khi mua một chiếc vali bất kì tại chi nhánh mới. Bác Bình mua 3 chiếc vali Samsonite với giá niêm yết cho một chiếc vali là \[5\,\,200\,\,000\] đồng. Với các hóa đơn trên \[10\,\,000\,\,000\] đồng, chi nhánh mới giảm thêm \[4\% \] trên tổng giá trị hóa đơn. Hỏi bác Bình phải thanh toán cho cửa hàng bao nhiêu tiền?
Một cửa hàng bán quần áo có chương trình khuyến mãu như sau: Khách hàng có thẻ thành viên sẽ được giảm \(15\% \) tổng số tiền của hóa đơn. Bạn Bình có thẻ thành viên, bạn mua hai chiếc sơ mi, mỗi áo đều có giá \(200{\rm{ 000}}\) đồng và một quần Jeans với giá \(350{\rm{ 000}}\). Bạn Bình đưa cho người thu ngân 1 triệu đồng. Hỏi bạn Bình được trả lại bao nhiêu tiền?
Một cửa hàng nhập một lô gồm 100 máy tính Casio với giá nhập là \(480{\rm{ 000}}\) đồng một sản phẩm. Sau đó khi bán 70 chiếc với tiền lãi bằng \(30\% \) giá nhập, cửa hàng bán số máy còn lại với giá bằng \(70\% \) giá bán trước đó. Hỏi sau khi bán hết lô hàng thì cửa hành lãi hay lỗ bao nhiêu tiền?
Một trường học cùng tham gia chương trình gây quỹ bằng cách tiết kiệm điện trong 15 ngày liên tiếp. Các nhân viên trong trường đưa ra hai phương án tiết kiệm điện như sau:
− Phương án 1: Ngày đầu tiên, trường tiết kiệm được \(\frac{1}{2}\) số điện, và ngày thứ hai trở đi, số điện tiết kiệm mỗi ngày gấp đôi ngày trước đó.
− Phướng án 2: Mỗi ngày trường đều tiết kiệm được 65 số điện.
Sau 15 ngày, điện lực sẽ quy đổi số điện mà nhóm tiết kiệm được thành tiền ủng hộ quỹ, với mức \(1{\rm{ }}000\) đồng/số.
Hỏi trường thực hiện phương án nào thì tiết kiệm được nhiều điện hơn? Và tiết kiệm được bao nhiêu tiền?


