Bài tập ôn tập Toán 12 Cánh diều Chương 5 có đáp án

Dạng 2. Trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Trong không gian với hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là mét), một ngọn hải đăng được đặt ở vị trí \(I\left( {10;\,\,20;\,\,30} \right)\) với bán kính phủ sáng là \(3\)km.

( a) Phương trình mặt cầu mô tả ranh giới bên ngoài của vùng phủ sáng trên biển của hải đăng là

\({\left( {x - 10} \right)^2} + {\left( {y - 20} \right)^2} + {\left( {z - 30} \right)^2} = {3000^2}\).

(b) Người đi biển ở vị trí \(A\left( {50;20;0} \right)\) nhìn thấy được ánh sáng của ngọn hải đăng.

(c) Người đi biển ở vị trí \(B\left( {4030;\,\,50;\,\,40} \right)\) nhìn thấy được ánh sáng của ngọn hải đăng.

(d) Nếu hai người đi biển có thể nhìn thấy ánh sáng của ngọn hải đăng thì khoảng cách giữa hai người đó không quá \(6\)km.

Bác An cần thiết kế một nhà vườn ngoài trời để trồng hoa. Bác đã thiết kế và vẽ mô hình nhà vườn trong hệ trục toạ độ \[Axyz\] như hình vẽ, với các cột nhà là các đoạn thẳng \[AA',\,BB',\,CC'\] và \[DD'\]. Phần mái là tứ giác \(A'B'C'D'\) và hình vuông \(ABCD\) nằm trên mặt đất. Biết độ dài các đoạn thẳng \(AB = 25\,{\rm{m}},AA' = BB' = 4\,{\rm{m}}\) và \(CC' = DD' = 3\,{\rm{m}}\).

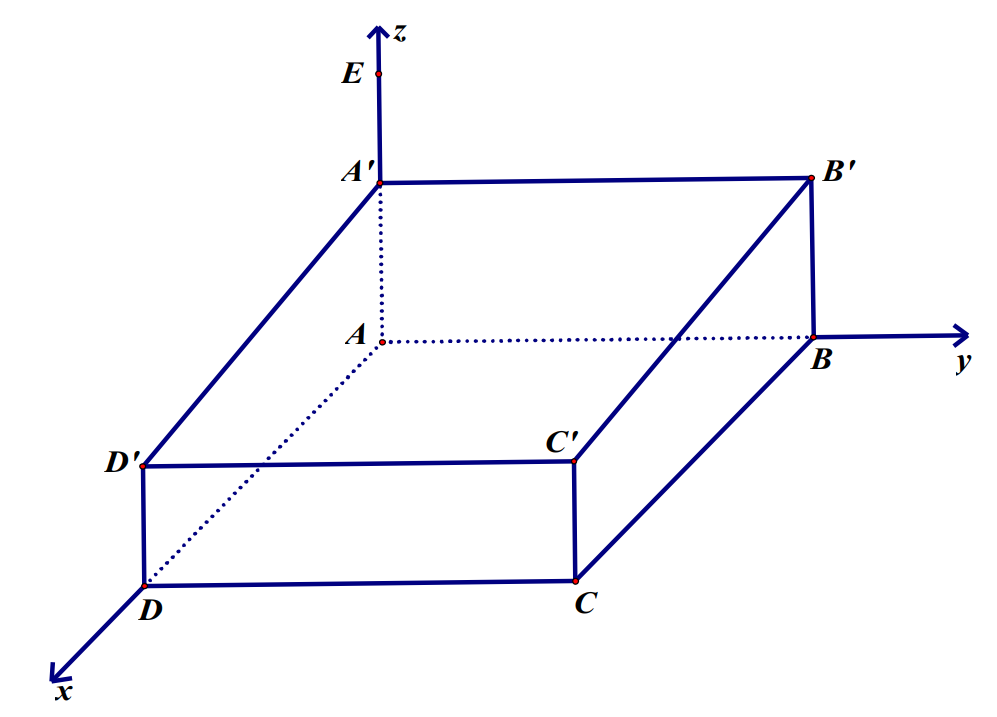
(a) Toạ độ điểm \(A'\left( {0;\,0;\,4} \right)\).

(b) Đường thẳng \(A'D'\) có phương trình tham số là \[\left\{ {\begin{array}{*{20}{c}}{x = 25t}\\{y = 0\,\,\,\,\,\,}\\{z = 4 - t}\end{array}\,\,\,\begin{array}{*{20}{c}}{}\\{,t \in \mathbb{R}}\\{}\end{array}} \right.\].

(c) Bác An đặt một camera ở vị trí \(E\) trên cột \(AA'\) và cách mặt đất \(7\,{\rm{m}}\). Một vật ở vị trí \(M\left( {a;\,b;\,c} \right)\) thoả mãn \(MA = MB = MC = MD = \sqrt {\frac{{697}}{2}} \) thì cách camera \(\frac{{\sqrt {1266} }}{2}{\rm{m}}\).

(d) Gọi \(\alpha \) là góc hợp bởi đường thẳng \(A'D'\) và mặt đất. Khi đó \(\cos \alpha = \frac{1}{{\sqrt {626} }}\,\).

Trong không gian với hệ tọa độ \(Oxyz\), một cabin cáp treo xuất phát từ điểm \(A\left( {10;3;0} \right)\) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\vec u = \left( {2; - 2;1} \right)\) với tốc độ \(4,5\)m/s (đơn vị trên mỗi trục tọa độ là mét).

(a) Phương trình tham số của đường cáp là: \(\left\{ \begin{array}{l}x = 10 + 2t\\y = 3 - 2t\\z = t\end{array} \right.\left( {t \in \mathbb{R}} \right)\).

(b) Giả sử sau thời gian \(t\)(s) kể từ lúc xuất phát \(\left( {t \ge 0} \right)\) thì cabin đến điểm \(M\). Khi đó tọa độ điểm \(M\) là \(M\left( {3t + 10; - 3t + 3;\frac{{3t}}{2}} \right)\).

(c) Cabin dừng ở điểm \(B\) có hoành độ \({x_B} = 550\), khi đó quãng đường \(AB\) dài 800 m.

(d) Đường cáp \(AB\) tạo với mặt phẳng \(\left( {Oxy} \right)\) một góc \(30^\circ \).

Trong không gian \[Oxyz\] (đơn vị trên mỗi trục tính theo kilômét), một trạm thu phát sóng điện thoại di động được đặt ở vị trí \[I\left( {1;\,3;\,7} \right)\]. Trạm thu phát sóng đó được thiết kế với bán kính phủ sóng là 3 km.

(a) Phương trình mặt cầu \[\left( S \right)\] để mô tả ranh giới bên ngoài của vùng phủ sóng trong không gian là \[{\left( {x + 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 7} \right)^2} = 9\].

(b) Nếu người dùng điện thoại ở vị trí điểm \[A\left( {2;\,2;\,7} \right)\] thì có thể sử dụng dịch vụ của trạm thu phát sóng đó.

(c) Nếu người dùng điện thoại ở vị trí có toạ độ \[B\left( {5;\,6;\,7} \right)\] thì không thể sử dụng dịch vụ của trạm thu phát sóng đó.

(d)Tính theo đường chim bay, khoảng cách lớn nhất để một người ở vị trí có toạ độ \[B\left( {5;\,6;\,7} \right)\] di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét là \[8\,\]km.

Trong không gian với hệ trục tọa độ \[Oxyz\], cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 2}}{1}\) và mặt phẳng \(\left( P \right): - x + 2y + z - 3 = 0\).

( a) Điểm \(A\left( {1;\, - 1;\, - 2} \right)\) nằm trên đường thẳng \(d\).

(b) Mặt phẳng \(\left( Q \right)\) song song với đường thẳng \(d\) và vuông góc với mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến là \(\left( {1;\,1;\, - 1} \right)\).

(c)Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) bằng \(30^\circ \).

(d) Đường thẳng \(\Delta \) đi qua điểm \(M\left( { - 3;\,1;\,2} \right)\), song song với mặt phẳng \(\left( P \right)\) và cắt đường thẳng \(d\) tại điểm \(N\left( {a;\,b;\,c} \right)\). Giá trị \(a + b + c\) bằng 3.

Trong không gian với hệ tọa độ \[Oxyz\], một viên đạn được bắn ra từ vị trí \(A\left( {1;2;3} \right)\) hướng đến vị trí \(B\left( {0;1; - 6} \right)\), bia chắn là mặt phẳng \(\left( P \right):4x - y + 2z + 13 = 0\), đơn vị là kilômét.

(a) Điểm \(B\) thuộc mặt phẳng \(\left( P \right)\).

(b) Giả sử viên đạn chuyển động thẳng đều theo hướng vectơ \(\vec v = \left( { - 2; - 2; - 18} \right)\) với vận tốc 800 m/s (bỏ qua mọi lực cản và chướng ngại vật), sau một phút viên đạn bắn ra đi qua điểm \(B\).

(c) Góc giữa đường thẳng \[AB\] và mặt phẳng \(\left( P \right)\) (làm tròn đến hàng đơn vị) là \(60^\circ \).

(d) Hình chiếu vuông góc của \(A\) trên \[\left( {Oxy} \right)\] là \(H\left( {0;2;3} \right)\).

Trong không gian hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu của một sân bay ở vị trí \(O\left( {0;0;0} \right)\) và được thiết kế phát hiện máy bay ở khoảng cách tối đa \(600\,{\rm{km}}\). Một máy bay đang chuyển động với vận tốc \(900\,\)km/h theo đường thẳng \(d\) có phương trình \[\left\{ \begin{array}{l}x = - 1000 + 100t\\y = - 300 + 80t\\z = 100\sqrt {11} \end{array} \right.\left( {t \in \mathbb{R}} \right)\] và hướng về đài kiểm soát không lưu (như hình vẽ).

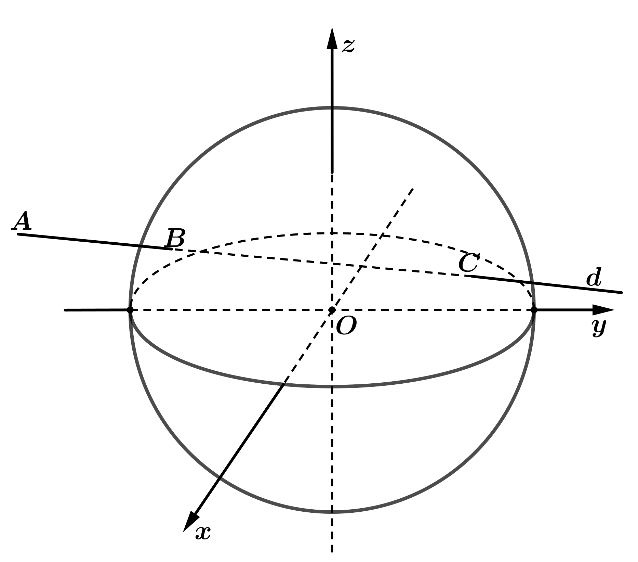
(a) Ranh giới vùng phát sóng bên ngoài của đài kiểm soát không lưu trong không gian là mặt cầu có bán kính bằng \(300\,\,{\rm{km}}\).

(b) Phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phát sóng của đài kiểm soát không lưu trong không gian là \({x^2} + {y^2} + {z^2} = 360000\).

(c) Máy bay đang chuyển động theo đường thẳng \(d\) đến vị trí điểm \(M\left( { - 500\,;\,100\,;\,100\sqrt {11} } \right)\). Vị trí này nằm ngoài vùng kiểm soát không lưu của đài kiểm soát không lưu sân bay.

(d) Thời gian kể từ khi đài kiểm soát không lưu phát hiện máy bay đến khi máy bay ra khỏi vùng kiểm soát không lưu là \(\frac{4}{3}\)giờ.

Một mái nhà hình tròn được đặt trên ba cây cột trụ. Các cây cột trụ vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là \[8{\rm{m}},\,9{\rm{m}},\,10{\rm{m}}\]. Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 8 m. Chọn hệ trục tọa độ như hình vẽ với \(B \in Ox\), \(C \in Oy\), tia \(Oz\) cùng hướng với vectơ \(\overrightarrow {AA'} \). Chọn gốc tọa độ \(O\) trùng với trung điểm của \(AC\) và mỗi đơn vị trên trục có độ dài 1m (xem hình vẽ).

(a) Tọa độ các điểm \(A'\left( {0; - 4;10} \right),B'\left( {4\sqrt 3 ;0;9} \right),C'\left( {0;4;8} \right)\).

(b) Mặt phẳng \(\left( {ABC} \right)\) nhận \(\overrightarrow k = \left( {0;\,1;\,1} \right)\)làm vectơ pháp tuyến.

(c) Mặt phẳng \(\left( {A'B'C'} \right)\) nhận \(\overrightarrow n = \left( {0;1;4} \right)\)làm vectơ pháp tuyến.

(d) Biết độ dốc của mái nhà đạt mức tiêu chuẩn khoảng từ \(27^\circ \) đến \(35^\circ \) thì mái nhà trên có độ dốc ở mức tiêu chuẩn.

Một khu bảo tồn thiên nhiên có hai trạm kiểm lâm và một trạm quan sát. Trong hệ toạ độ \(Oxyz\) (đơn vị độ dài trên mỗi trục là kilômét), hai trạm kiểm lâm và trạm quan sát có vị trí lần lượt là \(A\left( {10;5;0} \right)\), \(B\left( {70;85;0} \right)\) và \(I\left( {20;65;0,2} \right)\). Một thiết bị bay không người lái (drone) được thiết kế bay trên đường thẳng đi qua hai điểm \(C\left( {10;5;0,1} \right)\) và \(D\left( {70;85;0,1} \right)\) để truyền tín hiệu và dữ liệu về trạm quan sát \(I\).

(a)Khi tín hiệu gửi về trạm quan sát nhanh nhất thì vị trí của drone là \[K\left( {\frac{{212}}{5};\frac{{241}}{5};0,1} \right)\].

(b)Cùng một thời điểm, một xe máy xuất phát từ \(A\) đi đến \(B\) với vận tốc \(40\)km/h và một ô tô xuất phát từ \(B\) đi đến \(A\) với vận tốc \(60\)km/h, sau đó gặp nhau tại \(M\). Drone phải di chuyển trước đến vị trí \(H\) có hình chiếu trên \[AB\] là \(M\)để truyền dữ liệu về trạm quan sát \(I\). Khi đó vị trí của drone là \[\left( {34;37;0,1} \right)\].

(c)Trạm quan sát \(I\) nhìn đoạn thẳng \(AB\) dưới một góc nhỏ hơn \(65^\circ \).

(d)Phương trình đường thẳng mô tả cho tuyến đường bay của drone là \(\left\{ {\begin{array}{*{20}{l}}{x = 10 + 3t}\\{y = 5 + 4t}\\{z = 0,1}\end{array}} \right.\left( {t \in \mathbb{R}} \right)\).

Trong không gian với hệ trục tọa độ \(Oxyz\), có hai trục \(Ox,\;Oy\) đặt trên mặt đất (coi mặt đất là một mặt phẳng); tia \(Oz\) hướng lên phía trên; đơn vị trên các trục tính bằng mét. Một thiết bị phát sóng \(M\)đặt tại điểm \(A\left( {80;60;60} \right)\). Vùng phủ sóng của thiết bị \(M\) có bán kính \(500\) mét. Gọi \(d\) là đường thẳng đi qua điểm \(B\left( {0; - 490;0} \right)\) và song song với trục \(Ox.\)

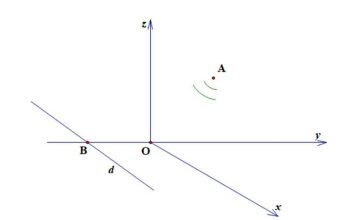
(a) Một thiết bị thu sóng \(N\)(coi như một điểm) di chuyển trên trục \(Oy\)từ vị trí \(B\) theo hướng của vectơ \(\overrightarrow {BO} \). Thiết bị thu sóng \(N\)phải di chuyển một đoạn đường ngắn nhất bằng \[60,3\]mét thì vào được vùng phủ sóng của thiết bị \[M\].

(b) Điểm \[B\] không thuộc vùng phủ sóng của thiết bị \[M\].

(c) Một thiết bị thu sóng \(N\)(coi như một điểm) di chuyển trên đường thẳng \(d\) thì có thể vào được vùng phủ sóng của thiết bị \[M\].

(d) Phương trình tham số của đường thẳng \(d\) là \[\left\{ \begin{array}{l}x = 0\\y = - 490\\z = t\end{array} \right.\left( {t \in \mathbb{R}} \right)\].

Dạng 3. Trắc nghiệm trả lời ngắn

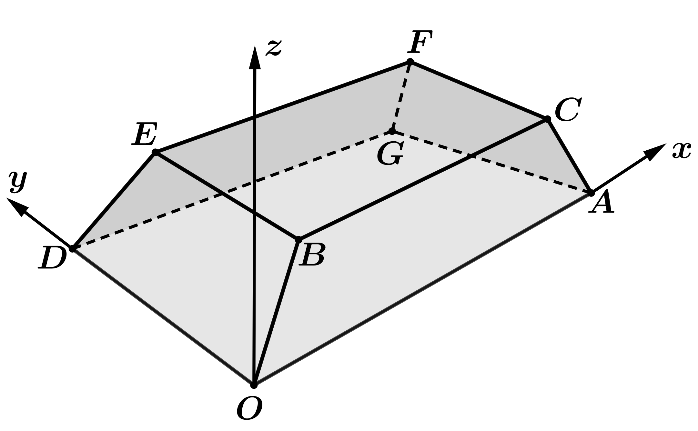
Một sân vận động được xây dựng theo mô hình là hình chóp cụt \[OAGD.BCFE\] có hai đáy song song với nhau. Mặt sân \(OAGD\) là hình chữ nhật và được gắn hệ trục \[Oxyz\] như hình vẽ (đơn vị trên mỗi trục tọa độ là mét). Mặt sân \[OAGD\] có chiều dài \[OA = 100\]m, chiều rộng \[OD = 60\]m và tọa độ điểm \[B\left( {10;10;8} \right)\]. Giả sử phương trình tổng quát của mặt phẳng \[\left( {OACB} \right)\] có dạng \[ax + y + cz + d = 0\]. Tính giá trị biểu thức \[a + c + d\].

Một phần sân trường được định vị bởi các điểm \(A,B,C,D\) như hình vẽ:

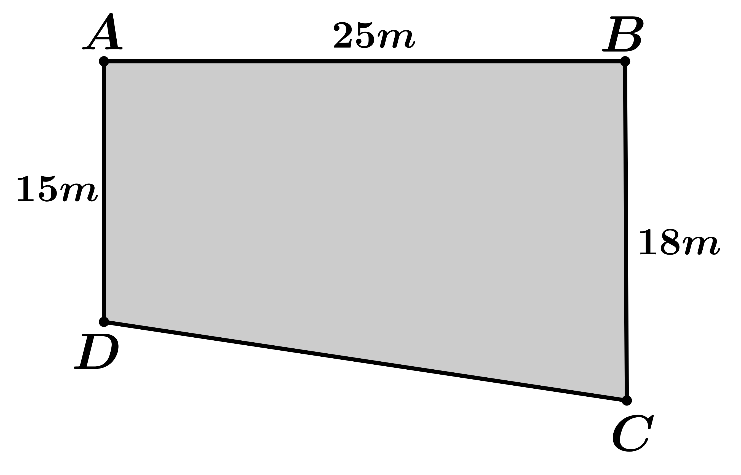
Bước đầu chúng được lấy “thăng bằng” để có cùng độ cao, biết \(ABCD\) là hình thang vuông ở \(A\) và \(B\) với độ dài \(AB = 25\,{\rm{m}}\), \(AD = 15\,{\rm{m}}\), \(BC = 18\,{\rm{m}}\). Do yêu cầu kĩ thuật, khi lát phẳng phàn sân trường phải thoát nước về góc sân ở \(C\) nên người ta lấy độ cao ở các điểm \(B\), \(C\), \(D\) xuống thấp hơn so với độ cao ở \(A\) là \(10\,{\rm{cm}}\), \(a\,\,{\rm{cm}}\), \(6\,{\rm{cm}}\) tương ứng. Giá trị của \(a\) bằng bao nhiêu?

Manhattanhenge (Hình 1) là một sự kiện diễn ra khi Mặt Trời mọc hoặc khi Mặt Trời lặn nằm thẳng hàng với các tuyến phố Đông - Tây thuộc mạng lưới đường phố chính tại quận Manhattan của thành phố New York. Khi mặt trời lặn, tia sáng song song mặt đất lệch một góc khoảng \(38^\circ \) so với hướng tây (Hình 2).

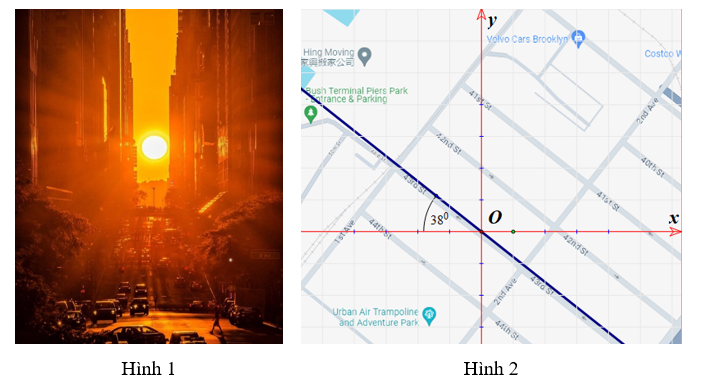
Giả sử mặt tiền các tòa nhà hai bên đường nằm trong 2 mặt phẳng song song cách nhau \(30\)m và vuông góc với mặt đất. Biết rằng mặt phẳng phía bắc đi qua gốc \(O\) của hệ trục \(Oxyz\), với tia \(Oz\) vuông góc với mặt đất và hướng lên trên. Phương trình mặt phẳng thứ hai có dạng \(\left( Q \right):x + ay + bz + c = 0\) với \(c = \frac{m}{{\sin n^\circ }}\). Tính \(m + n\).

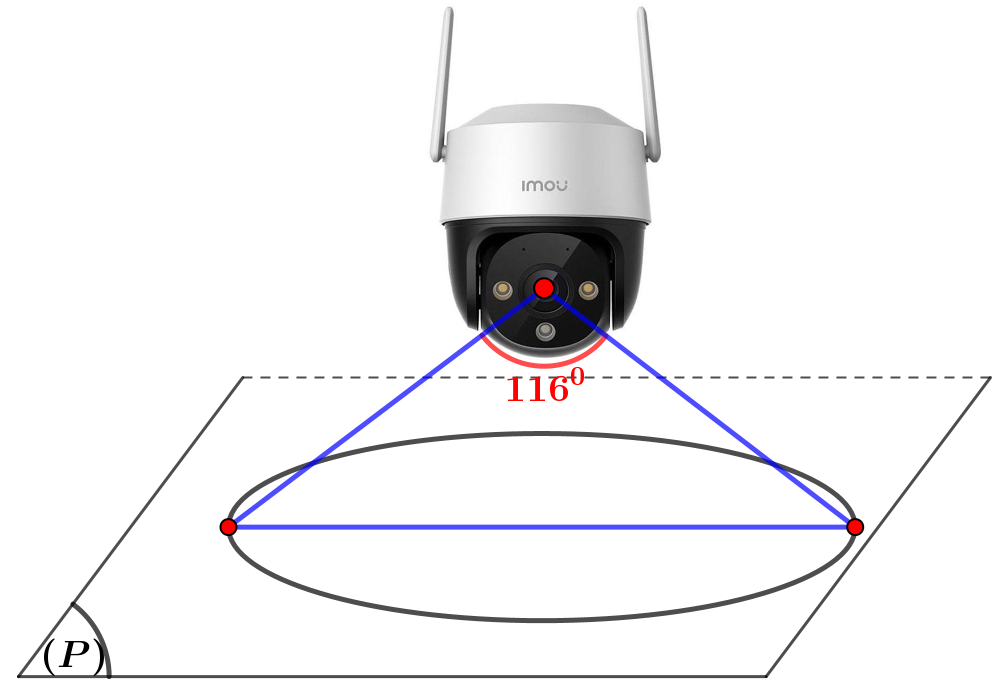
Biết góc quan sát ngang của một camera là \(116^\circ \). Trong không gian \(Oxyz\), camera được đặt tại điểm \(A\left( {2;1;5} \right)\) và chiếu thẳng về phía mặt phẳng \(\left( P \right):2x - y - 2z + 13 = 0\). Hỏi vùng quan sát được trên mặt phẳng \(\left( P \right)\) của camera là hình tròn có đường kính bằng bao nhiêu? (làm tròn kết quả đến chữ số hàng chục).

Hệ thống định vị toàn cầu GPS là một hệ thống cho phép xác định chính xác vị trí của một vật trong không gian. Cách thức hoạt động của GPS như sau: Trong cùng một thời điểm, vị trí \(M\) của một vật sẽ được xác định bằng 4 vệ tinh cho trước, các vệ tinh này có gắn máy thu tín hiệu, bằng cách so sánh thời gian từ lúc tín hiệu được phát đi với thời gian nhận tín hiệu phản hồi thì sẽ xác định được khoảng cách từ các vệ tinh đến vị trí \(M\). Như vậy, vị trí \(M\) là giao điểm của 4 mặt cầu có tâm là 4 vệ tinh đã cho. Giả sử trong không gian \(Oxyz\), 4 vệ tinh có tọa độ là \(A\left( { - 1;6;3} \right)\), \(B\left( {4;8;1} \right)\), \(C\left( {9;6;7} \right)\), \(D\left( { - 15;18;7} \right)\). Biết khoảng cách từ \(M\) đến các vệ tinh lần lượt là \(MA = 6\), \(MB = 7\), \(MC = 12\), \(MD = 24\). Khi đó tọa độ điểm \(M\left( {{x_M};\,{y_M};\,{z_M}} \right)\). Tính giá trị biểu thức \(T = {x_M} + {y_M} + {z_M}\).

Tại một nút giao thông có \[2\] con đường khác mức. Trên thiết kế, trong không gian Oxyz hai con đường đó thuộc hai đường thẳng \({d_1}:\frac{{x - 2}}{1} = \frac{{y - 2}}{1} = \frac{z}{{ - 1}}\); \({d_2}:\frac{{x - 2}}{1} = \frac{{y + 1}}{2} = \frac{z}{{ - 3}}\).

Người ta muốn tạo một con đường \(\Delta \) cắt \({d_1},\,{d_2}\) lần lượt tại \(A\) và \(B\) sao cho \(AB\) nhỏ nhất. Tính độ dài \(AB\), kết quả làm tròn đến hàng phần trăm.

Để xác định vị trí của máy bay khi đang bay, người ta gắn một hệ trục toạ độ \(Oxyz\) với gốc toạ độ đặt tại một sân bay để xác định toạ độ của sân bay. Biết rằng cao độ của toạ độ máy bay chính là độ cao của máy bay đối với mặt đất. Đơn vị độ dài trên mỗi trục toạ độ là 100 m.

Một máy bay đang bay với quỹ đạo là một đường thẳng trong không gian với vận tốc bay không đổi. Tại một thời điểm nào đó, máy bay đang ở vị trí có toạ độ \(\left( {200;70;118} \right)\). Sau 50 giây, độ cao của máy bay so với mặt đất giảm 400 m. Hỏi sau 25 giây nữa, khoảng cách từ sân bay tới máy bay là bao nhiêu kilomet, biết rằng trong suốt quá trình bay này, máy bay có đi qua điểm có toạ độ \(\left( {80;105;113} \right)\)?

Hệ thống định vị toàn cầu GPS hiện tại có 24 vệ tinh, mỗi vệ tinh cách trái đất 20000 km, ta coi Trái đất là một khối cầu có bán kính \(R = 6\)(nghìn km). Với hệ tọa độ \(Oxyz\) đã chọn, \(O\) là tâm trái đất và đơn vị trên mỗi trục là nghìn km, hai vệ tinh có tọa độ \(A\left( {26;0;0} \right)\), \(B\left( {0;26;0} \right)\). Xét điểm \(M\left( {x;y;z} \right)\) thuộc bề mặt Trái Đất. Tính giá trị nhỏ nhất của \(MA + MB\) theo đơn vị nghìn km (làm tròn đến hàng đơn vị).

Với hệ trục tọa độ \(Oxyz\) sao cho \(O\) nằm trên mặt nước, mặt phẳng \(\left( {Oxy} \right)\) là mặt nước, trục \(Oz\) hướng lên trên (đơn vị đo: mét), một con chim bói cá đang săn mồi ở vị trí \[C\] cách mặt nước \[5\,\,{\rm{m,}}\] cách mặt phẳng \(\left( {Oxz} \right),\left( {Oyz} \right)\) lần lượt là \(6\,\,{\rm{m}}\) và \(2\,{\rm{m}}\), từ vị trí này nó phóng thẳng xuống vị trí con cá ở vị trí \[A\], biết con cá cách mặt nước \(50\,\,{\rm{cm,}}\)cách mặt phẳng \(\left( {Oxz} \right),\left( {Oyz} \right)\) lần lượt là \(1\,{\rm{m}}\) và \(1,5\,{\rm{m}}\) (tham khảo hình vẽ).

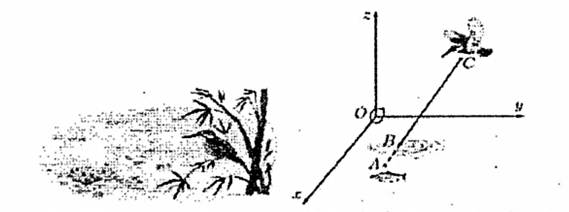
Giả sử vận tốc của con chim bói cá là \(4\,\,{\rm{m/s}}\), hỏi sau bao nhiêu giây thì nó chạm tới mặt nước (làm tròn đến hàng phần trăm)?

Hai chiếc flycam bay lên từ cùng một địa điểm. Sau một thời gian chiếc thứ nhất cách điểm xuất phát 300 m về phía Nam và 100 m về phía Đông, đồng thời cách mặt đất 100 m. Chiếc thứ hai nằm cách điểm xuất phát 200 m về phía Bắc và 100 m về phía Tây, đồng thời cách mặt đất 50 m. Cùng thời điểm đó, một người đứng trên mặt đất quan sát thấy hai chiếc flycamnói trên. Biết rằng, so với các vị trí quan sát trên mặt đất, vị trí người đứng có tổng khoảng cách đến hai chiếc flycam là nhỏ nhất. Tính khoảng cách từ vị trí người quan sát đến địa điểm xuất phát của hai chiếc flycam(kết quả làm tròn đến hàng đơn vị của mét).

B. Tự luận

Trong không gian \(Oxyz\)(đơn vị trên mỗi trục tọa độ là mét), một ngôi nhà như hình vẽ dưới đây có sàn nhà nằm trên mặt phẳng \(\left( {Oxy} \right)\). Hai mái nhà lần lượt nằm trên các mặt phẳng \(\left( P \right):\,\,x - 2y + 5 = 0\) và \(\left( Q \right):\,\,x - 2y - 3{\rm{z}} + 20 = 0\). Hỏi là chiều cao của ngôi nhà tính từ sàn nhà lên nóc nhà (điểm cao nhất của mái nhà) là bao nhiêu?

Trong không gian \(Oxyz\), một viên đạn được bắn ra từ điểm \(A\left( {1;\,3\,;4} \right)\) và trong 3 giây, đầu đạn đi với vận tốc không đổi, vectơ vận tốc (trên giây) là  \[\overrightarrow v = \left( {2;1;6} \right).\] Hỏi viên đạn trên có bắn trúng mục tiêu trong mỗi tình huống sau hay không?

(a) Mục tiêu đặt tại điểm  \(M\left( {7;\frac{7}{2};21} \right)\).

(b) Mục tiêu đặt tại điểm \(N\left( { - 3;\,1;\, - 8} \right)\).

Bác An dự định làm bốn mái nhà của một ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp tứ giác đều và các mái kề nhau thì vuông góc với nhau. Hỏi ý tưởng đó có làm được không?

Trên một cánh đồng điện năng lượng mặt trời, người ta đã thiết lập sẵn một hệ tọa độ \(Oxyz\). Hai tấm pin năng lượng lần lượt nằm trong hai mặt phẳng \(\left( P \right):2x + 2z + 1 = 0\) và \(\left( {P'} \right):x + z + 7 = 0\).

(a) Tính góc giữa \(\left( P \right)\) và \(\left( {P'} \right)\).

(b) Tính góc hợp bởi \(\left( P \right)\) và \(\left( {P'} \right)\) với mặt đất \(\left( Q \right)\) có phương trình \(z = 0\).