Bài tập ôn tập Toán 12 Cánh diều Chương 3 có đáp án
40 câu hỏi
A. Trắc nghiệm
Dạng 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau.

Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.
25.
30.
6.
69,8.
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Nhóm chứa tứ phân vị thứ nhất là
\([14;15)\).
\([15;16)\).
\([16;17)\).
\([17;18)\).
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Nhóm chứa tứ phân vị thứ ba là
\([15;16)\).
\([16;17)\).
\([17;18)\).
\([18;19)\).
Bảng dưới biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.
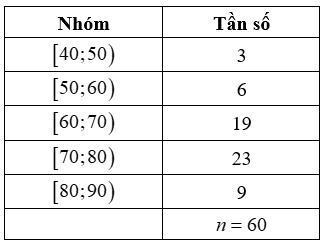
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
50.
30.
6.
69,8.
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khoẻ. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm là
1,5.
0,9.
0,6.
0,3.
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa tứ phân vị thứ nhất là
\([0;20)\).
\([20;40)\).
\([40;60)\).
[60; 80).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
7.
7,6.
8.
8,6.
Bạn Hà rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Hà được thống kê lại ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm là
25.
20.
15.
30.
Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik \(3 \times 3\), bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm nhận giá trị nào trong các giá trị dưới đây?
6.
8.
10.
12.
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
10.
11.
12.
13.
Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm này là
26.
15.
20.
12.
Bảng dưới biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.
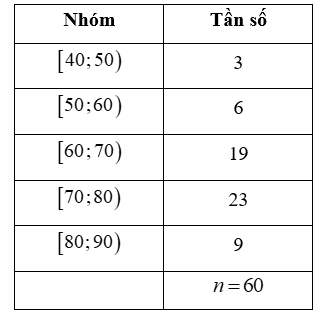
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:
50.
40.
14,23.
70,87.
Biểu đồ dưới đây biểu diễn số lượng khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý II năm 2025 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến 6 lượt đặt bàn, cột thứ hai biểu diễn số ngày có từ 6 đến 11 lượt đặt bàn; …
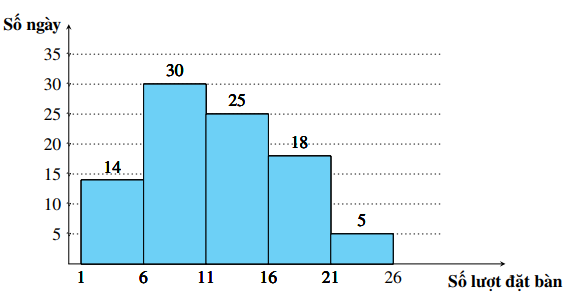
Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên là:
9,5.
8,5.
10,5.
7,5.
Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik \(3 \times 3\), bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
10,75.
1,75.
3,63.
14,38.
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Số trung bình của mẫu số liệu trên thuộc nửa khoảng nào trong các nửa khoảng dưới đây?
\[[7;9)\].
\([9;11)\).
\([11;13)\).
\([13;15)\).
Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng bằng 3 thì có phương sai bằng:
\({s^2} = \sqrt 3 .\)
\({s^2} = 3.\)
\[{s^2} = 9.\]
\({s^2} = 6.\)
Để đánh giá chất lượng của một loại pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn đến 4 chữ số thập phân).
\(0,4252\).
\(0,5314\).
\(0,6214\).
\(0,5268\).
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khoẻ. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:

Phương sai của mẫu số liệu ghép nhóm là
3,39.
11,62.
0,1314.
0,36.
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng dưới đây.
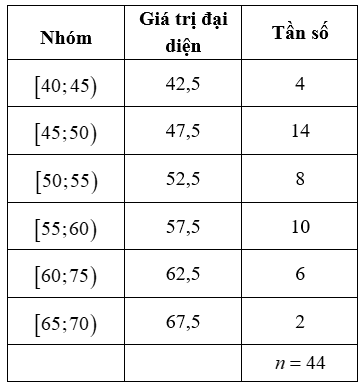
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
6,8.
7,3.
3,3.
46,1.
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng dưới đây.

Phương sai của mẫu số liệu ghép nhóm trên là:
53,2.
46,1.
30.
11.
Dạng 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Bảng sau biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.
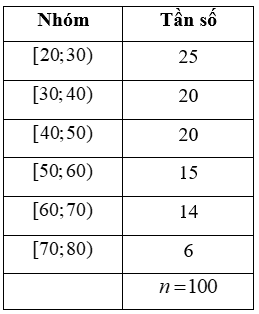
(a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = 60\).
(b) Tứ phân vị thứ nhất là: \({Q_1} = 35\).
(c) Tứ phân vị thứ ba là: \({Q_3} = \frac{{160}}{3}\).
(d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: \({\Delta _Q} = \frac{{65}}{3}\).
Giả sử kết quả khảo sát hai khu vực \(A\) và \(B\) về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

(a) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: \(15\) (tuổi).
(b) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: \(12\)(tuổi).
(c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm ứng với khu vực A là: \(\frac{{61}}{3}\) (tuổi).
(d) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn.
Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.
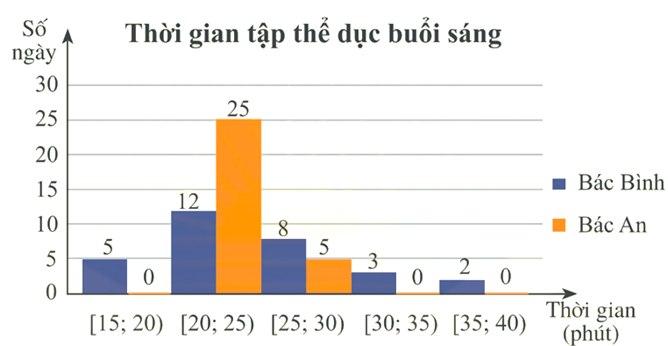
(a) Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là \(25\) (phút).
(b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An là: \({\Delta _Q} = 2\).
(c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là: \({Q_3}^\prime = \frac{{455}}{{16}}\).
(d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An lớn hơn bác Bình.
Kết quả \(40\) lần nhảy xa của hai vận động viên Dũng và Huy được lần lượt thống kê trong bảng bên dưới (đơn vị: mét).
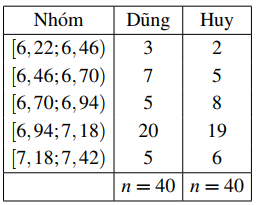
(a) Số trung bình cộng của mẫu số liệu ghép nhóm biểu diễn kết quả 40 lần nhảy xa của vận động viên Dũng cho bởi Bảng 15 (làm tròn kết quả đến hàng phần trăm) là \(6,92\)m.
(b) Độ lệch chuẩn của mẫu số liệu ghép nhóm biểu diễn kết quả 40 lần nhảy xa của vận động viên Dũng cho bởi Bảng 15 (làm tròn kết quả đến hàng phần trăm) là \(0,26\)m.
(c) Phương sai của mẫu số liệu ghép nhóm biểu diễn kết quả 40 lần nhảy xa của vận động viên Huy cho bởi Bảng 16 (làm tròn kết quả đến hàng phần trăm) là \(0,16.\)
(d) Kết quả nhảy xa của vận động viên Dũng đồng đều hơn kết quả nhảy xa của vận động viên Huy.
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình các tháng năm 2021 tại Hà Nội và Huế (đơn vị: độ C).
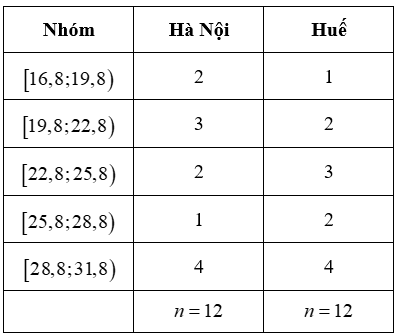
(a) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên số liệu ở Hà Nội là: \(8,75\).
(b) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên số liệu ở Hà Nội (làm tròn kết quả đến hàng phần trăm) là: \(3,56\).
(c) Phương sai của mẫu số liệu ghép nhóm trên số liệu ở Huế là: \(12,75\).
(d) Huế có nhiệt độ không khí trung bình tháng đồng đều hơn vì độ lệch chuẩn nhỏ hơn.
Một công ty giống cây trồng đã thử nghiệm hai phương pháp chăm sóc khác nhau cho cây
hướng dương. Sau hai tuần, người ta thấy cây được chăm sóc theo cả hai phương pháp đều thấp hơn 50 cm.
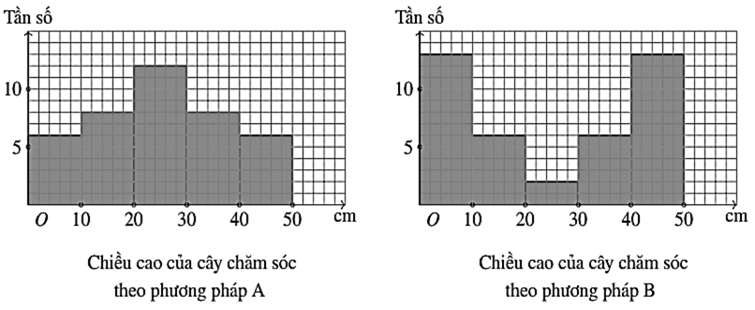
(a) Khoảng biến thiên của chiều cao các cây được chăm sóc theo mỗi phương pháp \(A\) và \(B\) bằng nhau.
(b) Trung bình của chiều cao các cây được chăm sóc theo mỗi phương pháp \(A\) và \(B\) bằng nhau.
(c) Độ lệch chuẩn của chiều cao các cây được chăm sóc theo phương án \(A\)là \(12,65\)(cm).
(d) Dựa vào độ lệch chuẩn thì chiều cao của các loại cây được chăm sóc theo phương án \(B\)ít bị chênh lệch hơn so với phương án \(A\).
Bảng sau thống kê lại tổng số giờ nắng trong tháng 6 của các năm từ 2002 đến 2021 tại hai trạm quan trắc đặt ở Nha Trang và Quy Nhơn.

(a) Xét số liệu ở Nha Trang thì khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(32,64\).
(b) Nếu so sánh theo khoảng tứ phân vị thì số giờ nắng trong tháng 6 của Quy Nhơn đồng đều hơn.
(c) Xét số liệu của Quy Nhơn ta có độ lệch chuẩn của mẫu số liệu ghép nhóm (làm tròn kết quả đến hàng phần trăm) là: \(30,59\).
(d) Nếu so sánh theo độ lệch chuẩn thì số giờ nắng trong tháng 6 của Nha Trang đồng đều hơn.
Dạng 3. Trắc nghiệm trả lời ngắn
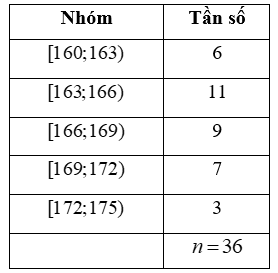
Bảng dưới biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị: centimét) của 36 học sinh nam lớp 12 ở một trường trung học phổ thông. Tìm khoảng biến thiên của mẫu số liệu ghép nhóm đó.
Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn;...
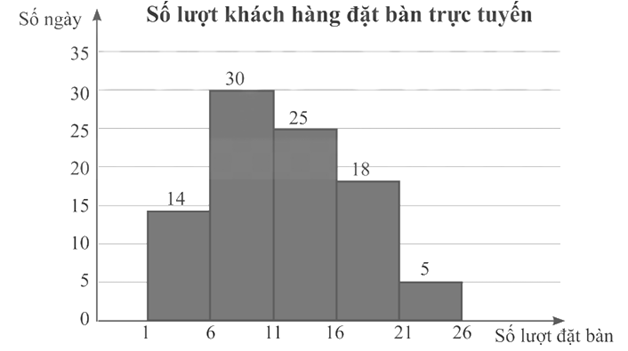
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được mô tả bằng biểu đồ sau.
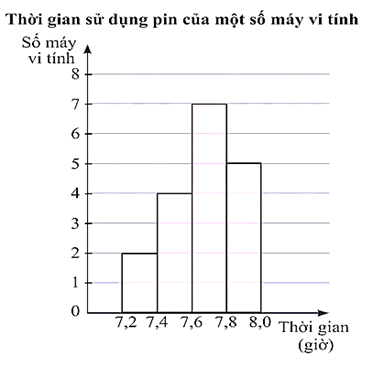
Hãy xác định độ lệch chuẩn của thời gian sử dụng pin (kết quả được làm tròn đến hàng phần trăm).
Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ sau:
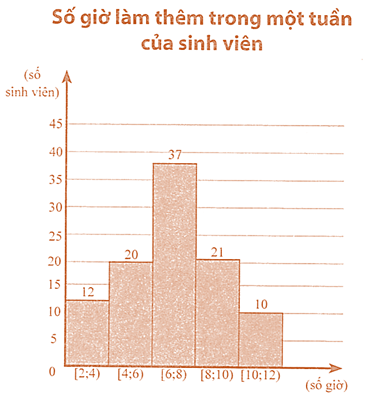
Tìm khoảng tứ phân vị của số liệu đó (làm tròn kết quả đến hàng phần trăm).
Người ta ghi chép lại trọng lượng (gam) một loại cá rô được nuôi trong ao theo một chế độ đặc biệt sau 6 tháng, họ có bảng tần số ghép nhóm sau:

Tìm phương sai của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị).
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh hoạ ở biểu đồ sau.
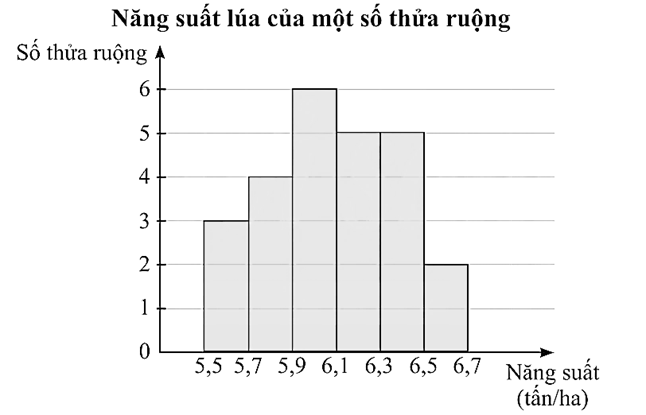
Người ta lập được bảng tần số ghép nhóm và tần số tương đối ghép nhóm tương ứng của mẫu số liệu trên như sau:
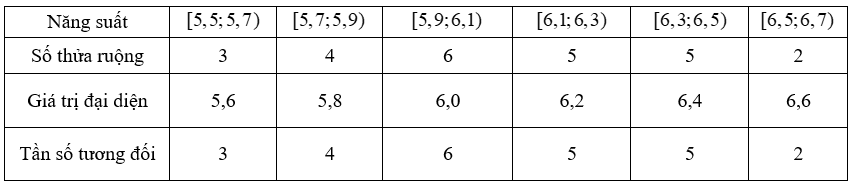
Hãy xác định độ lệch chuẩn của mẫu số liệu trên (làm tròn kết quả đến hàng phần trăm).
Cân nặng của một số quả mít trong một khu vườn được thống kê ở bảng sau:

Hãy tính phương sai của mẫu số liệu ghép nhóm trên. (Kết quả các phép tính làm tròn đến hàng phần mười)?
B. Tự luận
Để chuẩn bị mở một trung tâm thể dục thể thao, anh Dũng đã tiến hành điều tra tuổi thọ của máy chạy bộ do hai hãng \(X,Y\) sản xuất. Bảng dưới biểu thị hai mẫu số liệu mà anh thu thập được qua Internet.
Bảng: Tuổi thọ của máy chạy bộ (đơn vị: năm)

Khoảng biến thiên của mẫu số liệu nào lớn hơn? Từ đó có thể nói là máy chạy bộ do hãng nào sản xuất có tuổi thọ phân tán hơn?
Thời gian chờ khám bệnh của các bệnh nhân tại phòng khám \(X\) được cho trong bảng sau:

(a) Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm này.
(b) Từ một mẫu số liệu về thời gian chờ khám bệnh của các bệnh nhân tại phòng khám \(Y\) người ta tính được khoảng tứ phân vị bằng 9,23. Hỏi thời gian chờ của bệnh nhân tại phòng khám nào phân tán hơn?
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:

Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bản thống kê thời gian của \(100\) lần ông Thắng đi xe buýt từ nhà đến cơ quan.

(a) Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm phía trên (Làm tròn kết quả đến hàng phần trăm).
(b) Biết rằng trong \(100\) lần đi trên, chỉ có đúng một lần ông Thắng đi hết \(32\) phút. Thời gian của lần đi đó có phải giá trị ngoại lệ không?
Thống kê tổng số giờ nắng trong tháng 9 tại một trạm quan trắc đặt ở Cà Mau trong các năm từ 2002 đến 2021 được thống kê như sau:

(a) Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu trên.
(b) Hãy lập bảng tần số ghép nhóm với nhóm đầu tiên là \(\left[ {80;98} \right)\) và độ dài mỗi nhóm bằng 18. Tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm.
(c) Hãy tính sai số tương đối của độ lệch chuẩn của mẫu số liệu ghép nhóm so với độ lệch chuẩn của mẫu số liệu gốc.
(Kết quả các phép tính làm tròn đến hàng phần nghìn)
Biểu đồ dưới đây mô tả kết quả điều tra về mức lương khởi điểm (đơn vị: triệu đồng) của một số công nhân ở hai khu vực \(A\) và \(B\).
(a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu đó.
(b) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì công nhân ở khu vực nào có mức lương khởi điểm đồng đều hơn?
Mức lương khởi điểm của công nhân ở hai khu vực \(A\) và \(B\)