Bài tập ôn tập Toán 11 Chân trời sáng tạo Chương 1 có đáp án
55 câu hỏi
Chọn khẳng định đúng.
\(\sin \left( {\pi - \alpha } \right) = - \sin \alpha \).
\(\cot \left( {\pi - \alpha } \right) = \cot \alpha \).
\(\tan \left( {\pi - \alpha } \right) = \tan \alpha \).
\(\cos \left( {\pi - \alpha } \right) = - \cos \alpha \).
Đổi số đo của góc 70° sang đơn vị radian.
\(\frac{7}{{18}}\).
\(\frac{{7\pi }}{{18}}\).
\(\frac{{70}}{\pi }\).
\(\frac{7}{{18\pi }}\).
Đổi số đo của góc \(\frac{\pi }{{12}}\) rad sang đơn vị độ.
\(6^\circ \).
\(15^\circ \).
\(10^\circ \).
\(5^\circ \).
Chọn khẳng định đúng?
\(\frac{1}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha \left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\).
\(\frac{1}{{{{\tan }^2}\alpha }} = 1 + {\cot ^2}\alpha \left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\).
\({\sin ^2}a + {\cos ^2}b = 1\).
\({\cos ^4}\alpha + {\sin ^4}\alpha = 1\).
Cho \(P = \sin \left( {\pi + \alpha } \right)\cos \left( {\pi - \alpha } \right)\) và \(Q = \sin \left( {\frac{\pi }{2} - \alpha } \right)\cos \left( {\frac{\pi }{2} + \alpha } \right)\). Mệnh đề nào dưới đây là đúng?
\(P + Q = 0\).
\(P + Q = - 1\).
\(P + Q = 1\).
\(P + Q = 2\).
Cho \(\pi < \alpha < \frac{{3\pi }}{2}\). Khẳng định nào sau đây đúng?
A. \(\tan \left( {\frac{{3\pi }}{2} - \alpha } \right) < 0\).
B. \(\tan \left( {\frac{{3\pi }}{2} - \alpha } \right) > 0\).
C. \(\tan \left( {\frac{{3\pi }}{2} + \alpha } \right) > 0\).
D. \(\tan \left( {\pi - \alpha } \right) \ge 0\).
Rút gọn biểu thức \(A = \sin \left( {\pi + x} \right) + \cos \left( {\frac{\pi }{2} - x} \right) + \cot \left( {2\pi - x} \right) + \tan \left( {\frac{{3\pi }}{2} - x} \right)\). Chọn đáp án đúng?
\(A = - 2\sin x\).
\(A = - 2\cot x\).
\(A = 0\).
\(A = - 2\sin x - 2\cot x\).
Cho \(\alpha \in \left( {\frac{\pi }{2};\pi } \right)\) thỏa mãn \(\sin \alpha = \frac{3}{5}\). Tính giá trị biểu thức \(P = \cos \alpha \).
\(\frac{4}{5}\).
\( - \frac{4}{5}\).
\( - \frac{2}{5}\).
\(\frac{2}{5}\).
Giá trị của biểu thức \(\sin \frac{\pi }{5}.\cos \frac{\pi }{{30}} + \sin \frac{\pi }{{30}}\cos \frac{{4\pi }}{5}\) bằng
\(1\).
\(\frac{1}{2}\).
\(\sqrt 3 \).
\(0\).
Giá trị của biểu thức \(A = \frac{{\sin \frac{\pi }{9} + \sin \frac{{5\pi }}{9}}}{{\cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9}}}\) bằng
\(\frac{1}{{\sqrt 3 }}\).
\( - \frac{1}{{\sqrt 3 }}\).
\(\sqrt 3 \).
\( - \sqrt 3 \).
Rút gọn biểu thức \(A = \frac{{2{{\cos }^2}x - 1}}{{\sin x + \cos x}}\) (giả sử biểu thức A có nghĩa).
\(A = \cos x + \sin x\).
\(A = \cos x - \sin x\).
\(A = \sin x - \cos x\).
\(A = - \sin x - \cos x\).
Cho biết \(\tan x = 5\). Tính giá trị biểu thức \(Q = \frac{{3\sin x - 4\cos x}}{{\cos x + 2\sin x}}\).
\(Q = 1\).
\(Q = \frac{{19}}{{11}}\).
\(Q = - 1\).
\(Q = \frac{{11}}{9}\).
Chọn câu sai.
Hàm số \(y = \tan x\) là hàm số lẻ.
Hàm số \(y = \cot x\) là hàm số lẻ.
Hàm số \(y = \sin x\) là hàm số chẵn.
Hàm số \(y = \cos x\) là hàm số chẵn.
Chọn câu sai?
Hàm số \(y = \tan x\) tuần hoàn với chu kì \(2\pi \).
Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi \).
Hàm số \(y = \sin x\) tuần hoàn với chu kì \(2\pi \).
Hàm số \(y = \cos x\) tuần hoàn với chu kì \(2\pi \).
Điều kiện xác định của hàm số \(y = \frac{1}{{\tan x}}\) là
\(x \ne \frac{\pi }{2} + k\pi \).
\(x \ne \frac{\pi }{4} + k\pi \).
\(x \ne \frac{\pi }{2} + k\frac{\pi }{2}\).
\(x \ne k\pi \).
Chu kì của hàm số \(y = 3\sin \frac{x}{2}\) là
0.
\(2\pi \).
\(4\pi \).
\(\pi \).
Tập xác định của hàm số \(y = \frac{{1 - \sin x}}{{1 + \cos x}}\) là
\(D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ { - k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\pi + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\).
Giá trị lớn nhất của hàm số \(y = 3{\sin ^2}\left( {x + \frac{\pi }{{12}}} \right) + 4\) bằng
7.
1.
3.
4.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2\cos \left( {x + \frac{\pi }{3}} \right)\). Tính \(P = M - m\).
\(P = 2\sqrt 2 \).
\(P = 4\).
\(P = \sqrt 2 \).
\(P = 2\).
Nghiệm của phương trình \(\cos x = - \frac{1}{2}\) là
\(x = \pm \frac{{2\pi }}{3} + k2\pi \).
\(x = \pm \frac{\pi }{6} + k\pi \).
\(x = \pm \frac{\pi }{3} + k2\pi \).
\(x = \pm \frac{\pi }{6} + k2\pi \).
Nghiệm phương trình \(\sqrt 3 \tan 2x - 3 = 0\) là
\(x = \frac{\pi }{3} + k\frac{\pi }{2},k \in \mathbb{Z}\).
\(x = \frac{\pi }{3} + k\pi ,k \in \mathbb{Z}\).
\(x = \frac{\pi }{6} + k\frac{\pi }{2},k \in \mathbb{Z}\).
\(x = \frac{\pi }{6} + k\pi ,k \in \mathbb{Z}\).
Phương trình \(\cot \left( {x + 45^\circ } \right) = \frac{{\sqrt 3 }}{3}\) có nghiệm là
\(15^\circ + k180^\circ ,k \in \mathbb{Z}\).
\(30^\circ + k180^\circ ,k \in \mathbb{Z}\).
\(45^\circ + k180^\circ ,k \in \mathbb{Z}\).
\(60^\circ + k180^\circ ,k \in \mathbb{Z}\).
Chọn khẳng định đúng trong các khẳng định sau:
Phương trình \(\sin x = m\)có nghiệm khi và chỉ khi m > 1.
Phương trình \(\sin x = m\)có nghiệm khi và chỉ khi \(\left| m \right| > 1\).
Phương trình \(\sin x = m\)có nghiệm khi và chỉ khi \(m \le 1\).
Phương trình \(\sin x = m\)có nghiệm khi và chỉ khi \(\left| m \right| \le 1\).
Nghiệm của phương trình \(\sin 2x = 1\) là
\(x = \frac{\pi }{4} + k\pi \).
\(x = \frac{\pi }{4} + k2\pi \).
\(x = \frac{{k\pi }}{2}\).
\(x = \frac{\pi }{2} + k2\pi \).
Tìm số nghiệm thuộc đoạn \(\left[ {\pi ;2\pi } \right]\) của phương trình \(2\sin \left( {x + \frac{\pi }{3}} \right) = 0\).
0.
1.
2.
3.
Tổng các nghiệm của phương trình \(\tan x = \tan \frac{{3\pi }}{8}\) trên \(\left( {\frac{\pi }{4};2\pi } \right)\).
\(\frac{{7\pi }}{4}\).
\(\frac{{3\pi }}{8}\).
\(\frac{{11\pi }}{8}\).
\(\frac{{3\pi }}{4}\).
Cho đồ thị hàm số lượng giác ở hình sau
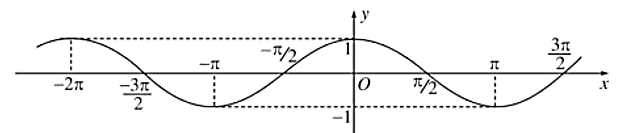
Khoảng đồng biến của hàm số là
\(\left( {\frac{{ - 3\pi }}{2}; - \pi } \right)\).
\(\left( { - \pi ;0} \right)\).
\(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
\(\left( { - \pi ;\pi } \right)\).
Nghiệm âm lớn nhất của phương trình \(\sqrt 3 \cot x = 1\) có giá trị bằng
\(\frac{{ - 2\pi }}{3}\).
\(\frac{\pi }{3}\).
\( - \frac{{4\pi }}{3}\).
\( - \frac{{14\pi }}{3}\).
Với \(k \in \mathbb{Z}\), phương trình \(\sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = \sin x\) có nghiệm là
\(x = \frac{\pi }{2} + k\pi \).
\(x = \frac{\pi }{4} + k\pi \).
\(x = \frac{\pi }{2} + k2\pi \).
\(x = \frac{\pi }{4} + k\frac{\pi }{2}\).
Phương trình \(\sin x = \sqrt 3 \cos x\) có bao nhiêu nghiệm trong khoảng \(\left( {0;\pi } \right)\)?
3.
2.
0.
1.
Cho biết \(\cos 2\alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\).
a) \(\sin \alpha < 0,\cos \alpha < 0\).
b) \(\sin \alpha = \frac{{\sqrt {10} }}{4}\).
c) \(\cos \alpha = \frac{{\sqrt 6 }}{4}\).
d) \(\cot \alpha = \frac{{\sqrt {15} }}{5}\).
Cho \(\cot x = - \sqrt 3 ,\frac{{3\pi }}{2} < x < 2\pi \).
a) \(\sin x = - \frac{{\sqrt {10} }}{{10}}\).
b) \(\cos x = \frac{{\sqrt 3 }}{{10}}\).
c) \(\sin \left( {\frac{{4\pi }}{3} - x} \right) = - \frac{{\sqrt {10} }}{5}\).
d) \(\tan \left( {x + \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{3}\).
Cho hàm số \(f\left( x \right) = \tan 2x - 1\). Khi đó:
Giá trị của hàm số \(f\left( x \right)\)tại \(x = \frac{\pi }{8}\) bằng 0.
Hàm số \(f\left( x \right)\)là hàm số chẵn.
Tập xác định của hàm số \(f\left( x \right)\) là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\) và tập giá trị là ℝ.
Hàm số \(f\left( x \right)\) là hàm số tuần hoàn.
Cho hàm số \(y = f\left( x \right) = 2{\sin ^2}x - 5\).
Hàm số tuần hoàn với chu kì \(2\pi \).
Hàm số là một hàm số chẵn.
Giá trị lớn nhất của hàm số đạt được khi \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Giá trị nhỏ nhất của hàm số bằng −3.
Cho hàm số \(f\left( x \right) = \tan \left( { - x} \right)\) xác định trên tập D.
Tập xác định của hàm số là D = ℝ.
\(y = \tan x,\forall x \in \mathbb{R}\).
\(f\left( x \right) = 1 \Leftrightarrow x = - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
Tổng các nghiệm của phương trình \(f\left( x \right) = 1\) trên đoạn \(\left[ { - \pi ;2\pi } \right]\) là \(\frac{{9\pi }}{4}\).
Số lượng (đơn vị: nghìn con) của một loài bướm ở một khu bảo tồn thiên nhiên được biểu diễn theo hàm số \(P\left( t \right) = 3 + 2\sin \left( {\frac{\pi }{6}t} \right)\), \(0 \le t \le 12\) với t tính theo tuần kể từ khi các nhà khoa học ước tính số lượng.
Số lượng bướm ban đầu là 5 nghìn con.
Số lượng bướm nhỏ nhất là 3 nghìn con.
Số lượng bướm luôn dao động từ 1 nghìn con đến 5 nghìn con.
Số lượng bướm lần đầu tiên chạm mức 4 nghìn con khi t = 5 tuần.
Cho hàm số \(f\left( x \right) = 4\sin x - 2\).
Tổng giá trị lớn nhất và nhỏ nhất của hàm số \(f\left( x \right) = 4\sin x - 2\) bằng −4.
Hàm số \(f\left( x \right) = 4\sin x - 2\) là hàm số chẵn.
Hàm số \(f\left( x \right) = 4\sin x - 2\) có tập xác định là ℝ.
\(f\left( {150^\circ } \right) = 0\).
Cho hàm số \(y = \sin x\).
Chu kì tuần hoàn của hàm số là \(T = 2\pi \).
Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
Tập giá trị của hàm số là \(T = \left[ { - 2;2} \right]\).
Tập nghiệm của phương trình \(\sin x = \frac{1}{2}\) là \(S = \left\{ {\frac{\pi }{4} + k2\pi ;\frac{{3\pi }}{4} + k2\pi ,k \in \mathbb{Z}} \right\}\).
Cho đồ thị hàm số \(y = f\left( x \right) = \sin x\) như hình vẽ

\(f\left( { - \frac{{3\pi }}{2}} \right) = - 1\).
Hàm số \(y = \sin x\) là hàm số lẻ trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\).
Trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\) phương trình \(\sin x = - \frac{1}{3}\) có 6 nghiệm phân biệt.
Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
Cho hàm số \(f\left( x \right) = \cos x\) và \(g\left( x \right) = \sin 5x\).
Tập nghiệm của phương trình \(f\left( x \right) = \frac{1}{2}\) là \(\left\{ {\frac{\pi }{3} + k2\pi ; - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}} \right\}\).
Số nghiệm của phương trình \(f\left( x \right) = \frac{1}{2}\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right]\) là 3.
Tổng các nghiệm của phương trình \(f\left( x \right) = \frac{1}{2}\)trên đoạn \(\left[ { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right]\) bằng \(4\pi \).
Tập nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là \(\left\{ {\frac{\pi }{{12}} + k\frac{\pi }{3};\frac{\pi }{8} + k\frac{\pi }{2},k \in \mathbb{Z}} \right\}\).
Cho \(\cos x = \frac{1}{3}\). Biểu thức \(P = {\sin ^2}x + 5{\cos ^2}x\) có giá trị bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Cho \(\alpha - \beta = \frac{\pi }{3}\). Tính giá trị của biểu thức \(A = {\left( {\cos \alpha + \cos \beta } \right)^2} + {\left( {\sin \alpha + \sin \beta } \right)^2}\).
Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng trong một phút. Chọn chiều quay của quạt là chiều dương. Biết rằng sau 5 giây, quạt quay được một góc có số đo là \(\frac{a}{b}\pi \) với \(a \in \mathbb{Z},b \in {\mathbb{N}^*},\frac{a}{b}\) là phân số tối giản. Tính b – a.
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm không nhuận được cho bởi một hàm số \(y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10\) với t ∈ ℕ và \(0 < t \le 365\). Gọi a là ngày có nhiều giờ có ánh sáng mặt trời nhất và b là ngày có ít giờ có ánh sáng mặt trời nhất trong năm. Tính a + b.
Biết rằng tổng các nghiệm của phương trình \(\sin 2x - \cos 2x - 5\sin x - \cos x + 3 = 0\) trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) là \(\frac{{a\pi }}{b}\) với \(a \in \mathbb{Z},b \in {\mathbb{N}^*},\frac{a}{b}\) là phân số tối giản. Tính a – b.
Gọi S là tổng các nghiệm thuộc đoạn \(\left[ {0;2025\pi } \right]\) của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = 0\). Khi đó \(\frac{{4S}}{{2025\pi }}\) bằng bao nhiêu?
Tập hợp các giá trị của tham số m để phương trình \(\sin 2x + 2 = m\)có nghiệm là \(\left[ {a;b} \right]\). Khi đó a + b bằng bao nhiêu?
Hằng năm, tại Hội Lim (huyện Tiên Du) thường có trò chơi đu. Giả sử một người chơi đu nhún đều làm cho cây đu đưa người đó dao động qua lại vị trí cân bằng, khoảng cách h từ người chơi đu đến vị trí cân bằng được xác định bởi \(h = \left| {3\cos \frac{{\left( {2t - 1} \right)\pi }}{3}} \right|\), với h tính bằng mét, thời gian t (t ≥ 0) tính bằng giây. Hỏi trong khoảng thời gian 10 giây đầu tiên, có bao nhiêu lần người chơi đu ở xa vị trí cân bằng nhất?
Cho hàm số \(y = \cos 2x - 2\cos x + 4\) có giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M và m. Tính \(M \cdot m\).
Phương trình \(\tan x = \sqrt 3 \)có bao nhiêu nghiệm trong khoảng \(\left( {0;\pi } \right)\)?
Cho \(\sin a = \frac{3}{5}\) và \(\frac{\pi }{2} < a < \pi \). Tính \(\cos a;\sin \left( {a + \frac{\pi }{4}} \right)\).
Rút gọn các biểu thức
(a) \(E = \frac{{1 - {{\sin }^2}\alpha {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} - {\cos ^2}\alpha \).
(b) \(F = 2\left( {{{\sin }^4}x + {{\cos }^4}x} \right) + 4{\sin ^2}x{\cos ^2}x\).
Giải các phương trình sau
(a) \(\sin \left( {3x - \frac{{7\pi }}{{12}}} \right) = \sin \left( { - x + \frac{\pi }{4}} \right)\);
(b) \(\sin 3x - \cos \left( {\frac{{3\pi }}{4} - x} \right) = 0\).
Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức \(h\left( t \right) = 30 + 20\sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right)\).
(a) Cabin đạt độ cao tối đa là bao nhiêu?
(b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?
Tính giá trị biểu thức \(A = {\sin ^2}10^\circ + {\sin ^2}20^\circ + ... + {\sin ^2}80^\circ \).


