Chuyên đề 8: Hình học (có đáp án)
191 câu hỏi
Cho điểm C thuộc nửa đường tròn đường kính AB. Kẻ tiếp tuyến Ax của nửa đường tròn đó (Ax nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng AB chứa nửa đường tròn). Tia phân giác của góc CAx cắt nửa đường tròn tại D. Kéo dài AD vafBC cắt nhau tại E. Kẻ EH vuông góc với Ax tại H.a) Chứng minh tứ giác AHEC nội tiếp đường tròn
b) Chứng minh
c) Chứng minh tam giác ABE cân
d) Tia BD cắt AC và Ax lần lượt tại F và K. Chứng minh AKEF là hình thoi
Cho nửa đường tròn (O;R) đường kính AB. Trên OA lấy điểm H (H khác O, H khác A). Qua H dựng đường thẳng vuông góc với AB, đường thẳng này cắt nửa đường tròn tại C. Trên cung BC lấy điểm M (M khác B, M khác C). Dựng CK vuông góc với AM tại K.
a) Chứng minh tứ giác ACKH nội tiếp đường tròn
b) Chứng minh
c) Gọi N là giao điểm của AM và CH. Tính theo R giá trị biểu thức
Cho nhọn (AB<AC) nội tiếp đường tròn (O). Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại D. OD cắt BC tại E. Qua D vẽ đường thẳng song song với AB, đường thẳng này cắt AC tại K. đường thẳng OK cắt AB tại F. Tính tỉ số diện tích
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (C) tâm O bán kính R. Hai đường cao AE và BK tam giác ABC cắt nhau tại H (với E thuộc BC, K thuộc AC).
1. Chứng minh rằng tứ giác ABEK nội tiếp được trong một đường tròn.
2. Chứng minh CE.CB=CK.CA
3. Chứng minh .
4. Cho B, C cố định và A di động trên (C) nhưng vẫn thỏa mãn điều kiện tam giác ABC nhọn; khi đó H thuộc cung tròn (T) cố định. Xác định I và bán kính r của đường tròn (T), biết R=3cm
Cho có ba góc nhọn (AB<AC), dựng AH vuông góc với BC tại điểm H. Gọi M, N theo thứ tự là hình chiếu vuông góc của H trên AB, AC. Đường thẳng MN cắt đường thẳng BC tại điểm D. Trên nửa mặt phẳng bờ CD chứa điểm A, vẽ nửa đường tròn đường kính CD. Qua B kẻ đường thẳng vuông góc với CD, cắt nửa đường tròn trên tại điểm E.
a.Chứng minh tứ giác AMHN là tứ giác nội tiếp.
b) Chứng minh
c) Chứng minh DM.DN=DB.DC
Gọi O là tâm đường tròn ngoại tiếp tam giác MNE. Chứng minh .
Cho tam giác ABC, M là điểm bất kỳ nằm trong tam giác. Kéo dài AM cắt BC tại P, BM cắt Q, CM cắt AB tại K. Chứng minh
Hai đường tròn (O) và (O') cắt nhau tại 2 điểm A, B. Gọi M là trung điểm OO'. Qua A kẻ đường thẳng vuông góc với AM cắt đường tròn (O) và (O') lần lượt ở C và D.Chứng minh rằng AC=AD
Cho đường tròn (O) đường kính AB, cung năm cùng phía đối với AB(D thuộc cung nhỏ ). Gọi E là giao điểm của AC và BD, F là giao điểm của AD và BC.
a.Tính góc khi số đo cung bằng 80o
b. Tính số đo cung khi góc .
Cho tam giác nhọn ABC(AB<AC). Đường tròn tâm (O) đường kính BC cắt AC, AB lần lượt tại D và E. H là giao điểm của BD và CE, K là giao điểm của DE và AH, I là giao điểm của AHvà BC, M là trung điểm của AH. Chứng minh rằng:
Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với đường tròn (A, B là hai tiếp điểm). Lấy điểm C trên cung nhỏ AB, (C không trùng với A và B). Từ điểm C kẻ CD vuông góc với AB, CE vuông góc với MA, CF vuông góc với MB . Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng
1) Tứ giác ADCE nội tiếp một đường tròn.
2) Hai tam giác CDE và CFD đồng dạng
3) Tia đối của tia CD là tia phân giác góc
4) Đường thẳng IK song song với đường thẳng AB
Cho đường tròn tâm O, đường kính AB. Trên tiếp tuyến của đường tròn (O) tại A lấy điểm M(M khác A ). Từ M vẽ tiếp tuyến thứ hai MC với đường tròn (O) (C là tiếp điểm). Kẻ (),MB cắt đường tròn (O) tại điểm thứ hai là K và cắt CH tại N. Chứng minh rằng:
a) Tứ giác AKNH nội tiếp trong một đường tròn.
b)
c)
d) N là trung điểm của CH
Cho tam giác AMB cân tại M nội tiếp đường tròn(O; R). Kẻ MH vuông góc với AB . MH cắt đường tròn tại N. Biết .
1. Tính MH và bán kính R của đường tròn.
Trên tia đối của tia BA lấy điểm C, MC cắt đường tròn tại D. ND cắt AB tại E. Chứng minh rằng tứ giác MDEH nội tiếp và chứng minh các hệ thức sau: và .
3. Chứng minh NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE
Cho tam giác ABC (AB<AC) nội tiếp đường tròn O. M là điểm nằm trên cung BC không chứa điểm A. Gọi D, E, F lần lượt là hình chiếu của M trên BC, CA, AB. Chứng minh rằng:a) Bốn điểm M, B, D, F cùng thuộc một đường tròn và bốn điểm M, D, E, C cùng thuộc một đường tròn.
b) Chứng minh D, E, F thẳng hàng
c)
Cho tam giác ABC vuông tại A, đường cao AH, Biết BH=4cm, CH=9cma) Tính độ dài đường cao AH và của tam giác ABC.
b) Vẽ đường trung tuyến của tam giác ABC, tính AM và diện tích tam giác AHM
Cho đường tròn (O) của đường kính AB. Vẽ tiếp tuyến Ax với đường tròn(O) ( A là tiếp điểm). Qua C thuộc tia Ax vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E ( D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Tứ giác AOHC nội tiếp.
b) Chứng minh: AC.AE=AD.CE
c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh: AM//BN
Cho tứ giác ABCD nội tiếp đường tròn tâm O, đường kính AD=2R..Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD tại F
1. Chứng minh ABEF nội tiếp.
2. Chứng minh
3. Tia BF cắt (O) tại K. Chứng minh EF//CK
4. Giả sử Tính theo R diện tích giới hạn dây BC và cung nhỏ BC.
Cho nửa đường tròn (O)đường kính MN=2R. Gọi (d) là tiếp tuyến của (O) tại N. Trên cung MN lấy điểm E tùy ý. (E không trùng với M và N), tia ME cắt đường thẳng (d) tại F. Gọi P là trung điểm của ME, tia OP cắt (d) tại Q.1. Chứng minh ONFP là tứ giác nội tiếp
2. Chứng minh OF MQ và PM.PF=PO.PQ
3. Xác định vị trí điểm E trên cung MN để tổng MF+2ME đạt giá trị nhỏ nhất.
Cho tam giác ABC vuông tại A. Biết AB=5cm; AC=12cm.a) Tính cạnh BC
Cho nửa đường tròn (O) đường kính AB. Từ A và B kẻ tiếp tuyến Ax và By (Ax và By cùng thuộc nửa mặt phẳng chứa nửa đường tròn (O)). Qua điểm M thuộc nửa đường tròn (M không trùng với A và B) kẻ tiếp tuyến thứ 3 cắt tiếp tuyến Ax và By lần lượt taị E và Fa) Chứng minh tứ giác AEMO là tứ giác nội tiếp.
b) AM cắt OE tại P, BM cắt OF tại Q. Chứng minh tứ giác MPOQ là hình chữ nhật.
Cho tam giác ABC có 3 góc nhọn. Đường tròn (O) đường kính BC cắt các cạnh AB, AC lần lượt tại các điểm D và E. Gọi H là giao điểm của hai đường thẳng CD và BE.a) Chứng minh tứ giác ADHE nội tiếp trong một đường tròn. Xác định tâm I của đường tròn này.
b) Gọi M là giao điểm của AH và BC. Chứng minh: CM.CB=CE.CA
c) Chứng minh ID là tiếp tuyến của đường tròn (O)
d) Tính theo R diện tích của tam giác ABC, biết , và BC=2R.
Cho tam giác ABC vuông tại A. Biết AN=5cm; AC=12 cm.a) Tính cạnh BC;
b) Kẻ đường cao AH. Tính AH
Cho nửa đường tròn (O) đường kính AB. Từ A và B kẻ tiếp tuyến Ax và By( Ax và By cùng thuộc nửa mặt phẳng chứa nửa đường tròn (O)). Qua điểm M thuộc nửa đường tròn (M không trùng với A và B) kẻ tiếp tuyến thứ 3 cắt tiếp tuyến Ax và By lần lượt tại E và F.a) Chứng minh tứ giác AEMO là tứ giác nội tiếp.
b) AM cắt OE tại P, BM cắt OF tại Q. Chứng minh tứ giác MPOQ là hình chữ nhật.
Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O;R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MQ). Dây cung PQ cắt OH và OM lần lượt tại I và K.
a. Chứng minh rằng tứ giác OMHQ nội tiếp.
2. Chứng minh rắng
3. Chứng minh rằng khi điểm M di chuyển trên đường thẳng d thì điểm I luôn cố định.
4. Biết , tính IP.IQ
Cho tam giác ABC (AB<AC) có ba góc nhọn nội tiếp đường tròn (O) và D là hình chiếu vuông góc của B trên AO sao cho D nằm giữa A và D. Gọi M là trung điểm của BC, N là giao điểm của BD và AC, F là giao điểm của MD và AC, E là giao điểm thứ hai của BD với đường tròn (O). H là giao điểm của BF và AD. Chứng minh rằng:
a) Tứ giác BDOM nội tiếp và .
b) DF song song với CE, từ đó suy ra NE.NF=NC.ND.
c) CA là tia phân giác góc
d) HN vuông góc với AB
Một cốc nước có dạng hình trụ có bán kính đáy bằng 3cm, chiều cao bằng 12cm và chứa một lượng nước cao 10cm. Người ta thả từ từ 3 viên bi làm bằng thủy tinh có cùng đường kính bằng 2cm vào cốc nước. Hỏi mực nước trong cốc lúc này cao bao nhiêu?
Cho nửa đường tròn tâm O đường kính AB=2R. Gọi M là điểm chính giữa của cung AB, N là điểm bất kỳ thuộc cung MB (N khác M và B). Tia AM và AN cắt tiếp tuyến tại B của nửa đường tròn tâm O lần lượt tại C và D
1. Tính số đo .
2. Chứng minh tứ giác MNDC nội tiếp một đường tròn
4. Chứng minh
Cho hình nón có đường sinh bằng 26cm diện tích xung quanh là Tính bán kính đáy và thể tích của hình nón.
Cho tam giác ABC nhọn có ba đường cao AD, BE, CF cắt nhau tại điểm H. Gọi M là trung điểm của đoạn AH.
1) Chứng minh tứ giác AEHF nội tiếp đường tròn.
2. Chứng minh CE.CA=CB.CD
3. Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF.
4) Gọi I và J lần lượt là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh .
Cho đường tròn (O) có AB là một dây cung cố định không đi qua O. Từ một điểm M bất kì trên cung lớn AB (M không trùng A và B) kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác AMN (Q thuộc AN).
a) Chứng minh tứ giác AMHQ nội tiếp đường tròn.
b) Gọi I là giao điểm của AB và MQ. Chứng minh tam giác IBM cân
c) Kẻ MP vuông góc với BN tại P. Xác định vị trí của M sao cho MQ.AN+MP.BN đạt giá trị lớn nhất.
Cho đường tròn (O), từ một điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB của đường tròn (A, B là hai tiếp điểm). Kẻ đường kính BE của đường tròn (O). Gọi F là giao điểm thứ hai của đường thẳng ME và đường tròn (O). Đường thẳng AF cắt MO tại điểm N. Gọi H là giao điểm của MO và AB.
1. Chứng minh tứ giác MAOB nội tiếp đường tròn.
2. Chứng minh AE//MO
3. Chứng minh
4. Chứng minh MN=NH
Cho đường tròn tâm O, đường kính AB cố định. H là điểm cố định thuộc đoạn OA(H không trùng O và A). Qua H vẽ đường thẳng vuông góc với AB cắt đường tròn tâm O tại C và D. Gọi K là điểm tùy ý thuộc cung lớn CD (K không trùng các điểm C, D và B). Gọi I là giao điểm của AK và CD.
a) Chứng minh tứ giác HIKB nội tiếp đường tròn.
b) Chứng minh AI.AK=AH.AB
c) Chứng minh khi điểm K thay đổi trên cung lớn CD của đường tròn tâm O thì tâm đường tròn ngoại tiếp tam giác KCl luôn thuộc một đường thẳng cố định
Cho đường tròn tâm O, bán kính R. Từ một điểm M ở ngoài đường tròn, kẻ hai tiếp tuyến MA và MB với đường tròn (A, B là các tiếp điểm). Qua A, kẻ đường thẳng song song với MO cắt đường tròn tại E (E khác A), đường thẳng ME cắt đường tròn tại F(F khác E), đường thẳng AF cắt MO tại N, H là giao điểm của MO và AB.
1. Chứng minh: Tứ giác MAOB nội tiếp đường tròn.
2. Chứng minh: và MN=NH
3. Chứng minh:
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
1) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.
2. Chứng minh
3. Chứng minh tứ giác BHIK là hình thoi.
d) Gọi P, Q lần lượt là tam của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.
Cho đường tròn tâm O, bán kính R, đường kính BC. Gọi A là một điểm thuộc đường tròn (A khác B và C). Đường phân giác cắt BC tại D và cắt đường tròn tại M
1. Chứng minh MB=MC và OM vuông góc với BC.
2. Gọi E, F lần lượt là hình chiếu của D lên AB, AC. Tứ giác AEDF là hình gì?
1. Cho tam giác ABC vuông tại A có AB=30 cm, AC=40 cm. Tính độ dài đường cao AH và số đo góc B (làm tròn đến độ).
2. Từ điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC với đường tròn (O), (B, C là hai tiếp điểm).
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho cát tuyến ADE nằm giữa 2 tia AO, AB; D, E thuộc đường tròn (O) và D nằm giữa A, E. Chứng minh .
c) Gọi F là điểm đối cứng của D qua AO,H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
1. Từ điểm M nằm bên ngoài đường tròn (O; R) vẽ các tiếp tuyến MA, MB (A, B là các tiếp điểm).
a) Chứng minh rằng bốn điểm M, A, O, B cùng nằm trên một đường tròn;
b) Vẽ cát tuyến MCD không đi qua tâm O của đường tròn đó sao cho điểm C nằm giữa hai điểm M và D. Tiếp tuyến tại điểm C và điểm D của đường tròn (O) cắt nhau tại điểm N. Gọi H là giao điểm của AB và MO, K là giao điểm của CD và QN. Chứng minh rằng
c) Chứng minh rằng ba điểm A, B, N thẳng hàng.
2. Hình trụ có đường kính đáy bằng 4cm và chiều cao bằng đường kính đáy. Tính thể tích hình trụ (lấy ).
Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn đó (C khác A, B). Lấy điểm D thuộc dây BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F.
a)Chứng minh rằng: Tứ giác FCDE là tứ giác nội tiếp đường tròn.
b) Chứng minh rằng: DA.DE=DB.DC
c) Gọi I là tâm đường tròn ngoại tiếp tứ giác FCDE, chứng minh rằng IC là tiếp tuyến của đường tròn (O)
Lúc 6h sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (như hình vẽ bên dưới). Cho biết đoạn thẳng AB dài 762m, góc A bằng 6o và góc B bằng 4o.

a) Tính chiều cao h của con dốc
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4km/h và tốc độ trung bình xuống dốc là 19km/h.
Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt các đoạn BC và OC lần lượt tại D và I gọi H là hình chiếu vuông góc của A lên OC; AH cắt BC tại M.
a) Chứng minh: Tứ giác ACDH là nội tiếp và .
b) Chứng minh: Hai tam giác OHB và OBC đồng dạng với nhau và HM là tia phân giác của góc BHD
c) Gọi K là trung điểm của BD chứng minh: MD.BC=MB.CD và MB.MD=MK.MC
d) Gọi E là giao điểm của AM và OK; J là giao điểm của IM và (O) (J khác I ).
Chứng Minh: Hai đường thẳng OC và EI cắt nhau tại một điểm trên (O).
Cho đường tròn (O) có tâm là điểm O, đường kính AB=2R. Trên đường thẳng lấy AB lấy H sao cho B nằm giữa A và H (H không trùng với B), qua H dựng đường thẳng d vuông góc với AB Lấy điểm C cố định thuộc đoạn thẳng OB (C không trùng với O và B). Qua điểm C kẻ đường thẳng a bất kỳ cắt đường tròn (O) tại hai điểm E, F (a không trùng với AB). Các tia AE và AF cắt đường thẳng d lần lượt tại M và N
a) Chứng minh rằng tứ giác BEMH nội tiếp đường tròn.
b) Chứng minh rằng tam giác AFB đồng dạng với tam giác AHN và đường tròn ngoại tiếp tam giác AMN luôn đi qua một điểm cố định khác A khi đường thẳng a thay đổi.
c) Cho AB=4cm, BC=1cm, HB=1cm Tìm giá trị nhỏ nhất của diện tích tam giác AMN
Cho tứ giác ABCD nội tiếp đường tròn đường kính AB. Hai đường chéo AC và BD cắt nhau tại E, F là hình chiếu vuông góc của E trên AB.
1. Chứng minh tứ giác ADEF nội tiếp.
2. Gọi N là giao điểm của CF và BD. Chứng minh BN.ED=BD.EN
Cho đường tròn (O;OA). Trên bán kính OA lấy điểm I sao cho . Vẽ dây BC vuông góc với OA tại điểm I và vẽ đường kính BD. Gọi E là giao điểm của AD và BC.
a) Chứng minh DA là tia phân giác của .
b) Chứng minh OE vuông góc với AD
c) Lấy điểm M trên đoạn AB (M khác I và B). Tia AM cắt đường tròn (O) tại điểm N. Tứ giác MNDE có phải là một tứ giác nội tiếp hay không? Vì sao?
Tính diện tích xung quanh, diện tích toàn phần và thể tích của một hình trụ có chu vi hình tròn đáy là 16 cm và chiều cao là 5 cm.
Cho hình vuông ABCD, điểm E thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc với DE, đường thẳng này cắt các đường thẳng DE và DC lần lượt tại H và K
a) Chứng minh tứ giác BHCD nội tiếp đường tròn.
b) Chứng minh tam giác KHC đồng dạng với tam giác KDB
c) Giả sử hình vuông ABCD có cạnh là 3cm. Tính độ dài cung CH có số đo bằng 40o của đường tròn đường kính BD (làm tròn kết quả đến một chữ số thập phân).
Cho tam giác ABC (AB<AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AB, AC theo thứ tự tại E, F. Gọi H là giao điểm của BF và CE, I là giao điểm của AH và BC. Từ A kẻ tiếp tuyến AN, AM đến đường tròn (O) với N, M là các tiếp điểm (N, B không cùng nửa mặt phẳng bờ AO).
a) Chứng minh các điểm A, I, M, N, O cùng thuộc một đường tròn
2. Chứng minh
c) Chứng minh ba điểm M, H, N thẳng hàng
Cho đường tròn (O;R) có dây MN cố định (MN<2R), P là một điểm trên cung lớn MN sao cho tam giác MNP có ba góc nhọn. Các đường cao ME và NK của tam giác MNP cắt nhau tại H.
a) Chứng minh rằng tứ giác PKHE nội tiếp đường tròn
c) Chứng minh rằng khi P thay đổi trên đường tròn (O) thì độ dài đoạn PH không đổi.
Cho hình vuông ABCD, gọi M và N lần lượt là trung điểm của BC và CD, gọi E là giao điểm của AM và BN. Chứng minh tứ giác ADNE nội tiếp đường tròn
Cho tam giác nhọn ABC nội tiếp đường tròn (O) (AB<AC). Gọi H là trực tâm tam giác ABC, gọi L là giao điểm của AH với đường tròn (O). Lấy điểm F bất kì trên cung nhỏ LC (không trùng với L và C). Lấy điểm K sao cho đường thẳng AClà trung trực của FK.
1) Chứng minh tứ giác AHCK nội tiếp đường tròn
2. Đường thẳng HK cắt AC tại điểm I, đường thẳng AF cắt HC tại G chứng minh AO vuông góc với GI.
Cho nửa đường tròn tâm O đường kính AB Dựng tiếp tuyến Ax (Ax và nửa đường tròn cùng thuộc nửa mặt phẳng bờ AB). C là một điểm nằm trên nửa đường tròn (C không trùng A, B), dựng tiếp tuyến Oy của nửa đường tròn (O) cắt Ax tại D. Kẻ , BD cắt (O) tại điểm thứ hai là K và cắt CH tại M. Gọi J là giao điểm của OD và AC.
a) Chứng minh rằng tứ giác AKMH nội tiếp được một đường tròn.
b) Chứng minh rằng tứ giác CKJM nội tiếp được một đường tròn .
c) Chứng minh rằng DJ là tiếp tuyến của đường tròn (O1)
Cho đường tròn (O) đường kính AB,lấy điểm C trên đường tròn (O) sao cho BC < AC. Gọi d là tiếp tuyến tại B của đường tròn (O), kẻ đường kính CD, các đường thẳng AC, AD lần lượt cắt d tại E,F. Đường thẳng qua A vuông góc với CD tại K cắt EF tại I
1) Chứng minh tứ giác OBIK nội tiếp.
2. Chứng minh AC.AE=AD.AF
3. Chứng minh I là trung điểm EF
Cho đường tròn (O) đường kính AC. Trên bán kính OC lấy điểm B tùy ý (điểm B không trùng O và C). Gọi M là trung điểm của đọan thẳng AB. Qua M kẻ dây cung DE vuông góc với AB. Kẻ BI vuông góc với CD .1. Cho AM=4cm, CM=9cm. Tính độ dài đoạn thẳng MD và tanA của
2. Chứng minh tứ giác BMDI nội tiếp.
3. Chứng minh tứ giác ADBE là hình thoi và ba điểm I, B, E thẳng hàng
4. Gọi O là tâm đường tròn đường kính BC. Chứng minh MI là tiếp tuyến của đường tròn O.
Cho tam giác ABC vuông tại A đường cao AH. đường tròn tâm E đường kính BH cắt AB tại M (M khác B), đường tròn tâm F đường kính HC cắt AC tại N (N khác C).
1. Chứng minh AM.AB=AN.AC và
2. Gọi I là trung điểm của EF, O là giao điểm của AH và MN. Chứng minh IO vuông góc với đường thẳng MN.
3. Chứng minh
Cho điểm M nằm bên ngoài đường tròn (O; R). Từ điểm M kẻ hai tiếp tuyến MA,MB với đường tròn đó ( A, B là các tiếp điểm ). Qua điểm A kẻ đường thẳng song song với MB cắt đường tròn (O;R) tại C. Nối MC cắt đường tròn (O; R) tại D. Tia AD cắt MB tại E .
a) Chứng minh MAOB là tứ giác nội tiếp.
b) Chứng minh EM=EB
c) Xác định vị trí của điểm M để
Cho đường tròn tâm O, bán kính R. Từ điểm C nằm ngoài đường tròn kẻ hai tiếp tuyến CA, CB và cát tuyến CMN với đường tròn (O) (A, B là hai tiếp điểm, M nằm giữa C và N). Gọi H là giao điểm của CO và AB.
a) Chứng minh tứ giác AOBC nội tiếp.
b) Chứng minh rằng: CH.CO=CM.CN
c) Tiếp tuyến tại M của đường tròn (O) cắt CA, CB theo thứ tự tại E, F. Đường thẳng vuông góc với CO tại O cắt CA, CB theo thứ tự tại P, Q. Chứng minh .
d) Chứng minh rằng:
Cho đường tròn tâm O, đường kính AB=2R và điểm M nằm trên đường tròn (MA<MB). Đường thẳng vuông góc với AB tại O cắt BM tại N và cắt tia AM tại C1. Chứng minh tứ giác AOMN nội tiếp được một đường tròn
2. Chứng minh rằng: MN.NB=ON.NC
3. Tính góc , tính diện tích tam giác ABC theo R.
Cho tứ giác ABCD nội tiếp. Gọi I là giao điểm của AC và BD. Kẻ
a)Chứng minh rằng tứ giác AHIK nội tiếp.
b) Chứng minh rằng: IA.IC=IB.ID
c) Chứng minh rằng tam giác HIK và tam giác BCD đồng dạng.
d) Gọi S là diện tích tam giác ABD, S' là diện tích tam giác HIK. Chứng minh rằng
Cho đường tròn tâm O, đường kính AB=2R, C là điểm chính giữa cung AB. Hai tiếp tuyến với đường tròn (O) tại A và C cắt nhau ở D.
1. Chứng minh AOCD là hình vuông.
2. Tính diện tích phần nằm ngoài hình thang ABCD của hình tròn (O) theo R
3. Trên đoạn DC lấy điểm E sao cho . Trên đoạn BC lấy điểm F sao cho EF=EA. Kẻ FG vuông góc với đường thẳng DC (). Tính độ dài đoạn thẳng CG theo R.
4. Chứng minh AECF nội tiếp
Cho nửa đường tròn (O; R) đường kính AB. Một điểm M cố định thuộc đoạn thẳng OB Đường thẳng d vuông góc với AB tại M cắt nửa đường tròn đã cho tại N. Trên cung NB lấy điểm E bất kì Tia BE cắt đường thẳng d tại C đường thẳng AC cắt nửa đường tròn tại D Gọi H là giao điểm của AE và đường thẳng d
a) Chứng minh tứ giác BMHE nội tiếp được đường tròn.
b) Chứng minh 3 điểm B, H, D thẳng hàng.
c) Tính giá trị của biểu thức theo R
d) Đường tròn ngoại tiếp tam giác AHC cắt AB tại K. Chứng minh rằng khi E di động trên cung NB thì độ dài đoạn thẳng BK không đổi.
Cho đường tròn tâm O đường kính AB và điểm C(C không trùng với A và B ). Lấy điểm D thuộc đoạn AC (D không trùng với A và C). Tia BD cắt cung nhỏ AC tại điểm M, tia BC cắt tia AM tại điểm N.
1. Chứng minh MNCD là tứ giác nối tiếp.
2. Chứng minh AM.BD=AD.BC
3. Gọi I là giao điểm thứ hai của hai đường tròn ngoài tiếp của tam giác ADM và tam giác BCD. Chứng minh ba điểm N, D, I thẳng hàng
Cho đường tròn (O) đường kính AB=2a, H là trung điểm của đoạn thẳng OA. Đường thẳng OA. Đường thẳng d vuông góc với OA tại H và cắt đường tròn (O) tại hai điểm C, D.a) Tính độ dài đoạn thẳng CD theo a.
b) Lấy điểm E trên cung nhỏ BD của đường tròn (O) sao cho ba điểm C, O, E không thẳng hàng (E khác B, E khác D). Gọi M, N lần lượt là trung điểm của AC và CE; K là hình chiếu vuông góc của A lên CE. Chứng minh BE song song với KH và MN là đường trung trực của đoạn thẳng KH.
c) Gọi I, J lần lượt là trung điểm của BC và BD. Đường tròn đường kính AI cắt các đoạn thẳng HB, Ạ, HD lần lượt tại P, F, Q (F khác A). Gọi L là giao điểm của IF và PQ. Chứng mih JL vuông góc với BD.
Cho đường tròn (O) có tâm O, đường kính BC. Lấy một điểm A trên đường tròn (O) sao cho AB>AC. Từ A, vẽ AH vuông góc với BC (H thuộc BC). Từ H, vẽ HE vuông góc với AB và HF vuông góc với AC (E thuộc AB, F thuộc AC).
a) Chứng minh rằng AEHF là hình chữ nhật và OA vuông góc với EF.
b) Đường thẳng EF cắt đường tròn (O) tại P và Q (E nằm giữa P và F). Chứng minh . Suy ra APH là tam giác cân.
c) Gọi D là giao điểm của PQ và BC; K là giao điểm của AD và đường tròn (O) (K khác A). Chứng minh AEFK là một tứ giác nội tiếp
d) Gọi I là giao điểm của KF và BC. Chứng minh
Cho tam giác ABC không có góc tù (AB<AC), nội tiếp đường tròn (O;R) (B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC), cắt BC tại F, cắt AC tại I
a) Chứng minh . Từ đó suy ra MBIC là tứ giác nội tiếp.
b) Chứng minh: FI.FM=FD.FE
c) Đường thẳng OI cắt (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt (O) tại T (T khác Q). Chứng minh ba điểm P, T, M thẳng hàng
d) Tìm vị trí điểm A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất.
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Biết AB=a, BC=2a. Tính theo a độ dài AC và AH.
Cho tam giác ABC có tù. Trên cạnh BC lấy hai D và E, trên cạnh AB lấy điểm F, trên cạnh AC lấy điểm K sao cho BD=BA, CE=CA, BE=BF, CK=CD. Chứng minh bốn điểm D, E, F và K cùng nằm trên một đường tròn.
Cho tam giác ABC(AB<AC) nội tiếp đường tròn đường kính BC, có đường cao AH (H thuộc cạnh BC), đường phân giác trong của góc A trong tam giác ABC cắt đường tròn đó tại K (K khác A). Biết .Tính
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O; R). Các đường cao BE và CF cắt nhau tại H.a) Chứng minh AEHF và BCEF là các tứ giác nội tiếp đường tròn.
b) Gọi M và N theo thứ tự là giao điểm thứ hai của đường trón (O; R) với BE và CF. Chứng minh MN//EF
d) Chứng minh rằng OA EF
Một bình hình trụ có đường kính đáy 1dm, chiều cao 2dm bên trong có chứa viên bi hình cầu có bán kính 4 cm. Hỏi phải đổ vào bình bao nhiêu lít nước để nước đầy bình. Cho biết:
với r là bán kính đáy; h là chiều cao hình trụ.
với R là bán kính hình cầu.
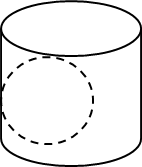
Kính lão đeo mắt của người già thường là loại thấu kính hội tụ. Bạn An đã dùng một chiếc kính lão của ông ngoại để tạo ra hình ảnh của một cây nến trên một tấm màn. Xét cây nến là một vật sáng có hình dạng là đoạn AB đặt vuông góc với trục chính của một thấu kính hội tụ, cách thấu kính một đoạn OA=2cm. Thấu kính có quang tâm O và tiêu điểm F. Vật AB cho ảnh thật A'B' gấp 3 lần AB. Tính tiêu cự (OF') của thấu kính ? Biết rằng đường đi của tia sáng được mô tả trong hình vẽ sau :
Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O) có AD, BE là hai đường cao cắt nhau tại H, vẽ đường kính AK của đường tròn (O), kẻa) Chứng minh 5 điểm A, B, D, E, F cùng thuộc một đường tròn, xác định tâm I của đường tròn này.
b) Gọi M là trung điểm của BC. Chứng minh 3 điểm H, M, K thẳng hàng.
c) Chứng minh IM là đường trung trực của DF








