34 câu hỏi
Hàm số \(F\left( x \right) = {e^{{x^2}}}\) là nguyên hàm của hàm số nào trong các hàm số sau?
\(f\left( x \right) = 2x{e^{{x^2}}}\).
\(f\left( x \right) = {x^2}{e^{{x^2}}} - 1\).
\(f\left( x \right) = {e^{2x}}\).
\(f\left( x \right) = \frac{{{e^{{x^2}}}}}{{2x}}\).
Tìm nguyên hàm \(\int {\frac{{\cos 2x}}{{{{\sin }^2}x{{\cos }^2}x}}{\rm{d}}x} \).
\(F\left( x \right) = - \cos x - \sin x + C\).
\(F\left( x \right) = \cos x + \sin x + C\)
\(F\left( x \right) = \cot x - \tan x + C\).
\(F\left( x \right) = - \cot x - \tan x + C\).
Gọi S là diện tích của hình phẳng giới hạn bởi các đường . Mệnh đề nào dưới đây là sai?
\(S = \int\limits_0^2 {\left| {{2^x} - 1} \right|{\rm{d}}x} \).
\(S = \int\limits_0^2 {\left| {1 - {2^x}} \right|{\rm{d}}x} \).
\(S = \int\limits_0^2 {\left( {1 - {2^x}} \right){\rm{d}}x} \).
\(S = \int\limits_0^2 {\left( {{2^x} - 1} \right){\rm{d}}x} \).
Thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = x + 1\), trục hoành và hai đường thẳng \(x = - 1,\,x = 2\) quanh trục hoành là:
\(V = \int\limits_{ - 1}^2 {{{\left( {x + 1} \right)}^2}{\rm{d}}x} \).
\(V = \pi \int\limits_{ - 1}^2 {{{\left( {x + 1} \right)}^2}{\rm{d}}x} \). x
\(V = \pi \int\limits_{ - 1}^2 {{{\left( {x + 1} \right)}^2}{\rm{d}}x} \).
\(V = \int\limits_{ - 1}^2 {\left| {x + 1} \right|{\rm{d}}x} \).D. \(V = \pi \int\limits_{ - 1}^2 {\left| {x + 1} \right|{\rm{d}}x} \).
Một chiếc xe ô tô đang chạy trên đường cao tốc với vận tốc \(72\,{\rm{km/h}}\) thì tài xế bất ngờ đạp phanh làm cho chiếc ô tô chuyển động chậm với gia tốc \(a\left( t \right) = - \frac{8}{5}t{\rm{ }}\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), trong đó \(t\) là thời gian tính bằng giây. Hỏi kể từ khi đạp phanh đến khi ô tô dừng hẳn thì ô tô di chuyển bao nhiêu mét? (Giả sử trên đường ô tô di chuyển không có gì bất thường).
\(50{\rm{ m}}\).
\(\frac{{250}}{3}{\rm{ m}}\).
\(\frac{{200}}{3}{\rm{ m}}\).
\(\frac{{100}}{3}{\rm{ m}}\).
Cho \(\int {f\left( x \right){\rm{d}}x} = {F_1}\left( x \right)\), \(\int {g\left( x \right){\rm{d}}x} = {F_2}\left( x \right)\). Tính \[I = \int {\left[ {2g\left( x \right) - f\left( x \right)} \right]{\rm{d}}x} \].
\(2{F_1}\left( x \right) - {F_2}\left( x \right) + C\).
\({F_2}\left( x \right) - {F_1}\left( x \right) + C\).
\(2{F_2}\left( x \right) - {F_1}\left( x \right) + C\).
\(\left| {{F_1}\left( x \right) + {F_2}\left( x \right)} \right| + C\).
Cho \(\int {{5^x}{\rm{d}}x} \, = F\left( x \right) + C\). Khẳng định nào dưới đây đúng?
\(F'\left( x \right) = {5^x}\ln 5\).
\(F'\left( x \right) = {5^x} + C\).
\(F'\left( x \right) = - {5^x}\).
\(F'\left( x \right) = {5^x}\).
Tìm nguyên hàm của hàm số \(f\left( x \right) = \frac{{{x^4} + 2}}{{{x^2}}}\).
\(\int {f\left( x \right){\rm{d}}x = } \frac{{{x^3}}}{3} - \frac{1}{x} + C\).
\(\int {f\left( x \right){\rm{d}}x = } \frac{{{x^3}}}{3} + \frac{2}{x} + C\).
\(\int {f\left( x \right){\rm{d}}x = } \frac{{{x^3}}}{3} + \frac{1}{x} + C\).
\(\int {f\left( x \right){\rm{d}}x = } \frac{{{x^3}}}{3} - \frac{2}{x} + C\).
Hàm số \(F\left( x \right) = x\sin x + \cos x + 2024\) là một nguyên hàm của hàm số nào trong các hàm số sau?
\(f\left( x \right) = x\sin x\).
\(f\left( x \right) = - x\cos x\).
\(f\left( x \right) = - x\sin x\).
\(f\left( x \right) = x\cos x\).
Cho hàm số \(f\left( x \right) = 2x + {e^x}\). Tìm một nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right)\) thoả mãn \(F\left( 0 \right) = 2024\).
\(F\left( x \right) = {x^2} + {e^x} + 2023\).
\(F\left( x \right) = {x^2} + {e^x} - 2023\).
\(F\left( x \right) = {x^2} + {e^x} + 2022\).
\(F\left( x \right) = {x^2} + {e^x} - 2024\).
Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{x} + \sin x\) là
\(\ln x - \cos x + C\).
\( - \frac{1}{{{x^2}}} - \cos x + C\).
\(\ln \left| x \right| + \cos x + C\).
\(\ln \left| x \right| - \cos x + C\).
Họ nguyên hàm của hàm số \[y = {e^x}\left( {2 + \frac{{{e^{ - x}}}}{{{{\cos }^2}x}}} \right)\] là
\[2{e^x} + \tan x + C\].
\[2{e^x} - \tan x + C\].
\[2{e^x} - \frac{1}{{\cos x}} + C\].
\[2{e^x} + \frac{1}{{\cos x}} + C\].
\[\int {\left( {{5^{2x}} - 6{e^{ - \frac{x}{2}}}} \right){\rm{d}}x} \] bằng
\[{e^x} - \frac{1}{2}{e^{ - 2x}} + C\].
\[\frac{{{{25}^x}}}{{2\ln 5}} + 12{e^{ - \frac{x}{2}}} + C\].
\[{e^x} - 2{e^{ - 2x}} + C\].
\[\frac{{{e^{x + 1}}}}{{x + 1}} + \frac{{{e^{ - 2x + 1}}}}{{ - 2x + 1}} + C\].
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = {e^{2x}}\) và \(F\left( 0 \right) = 0\). Giá trị của \(F\left( {\ln 3} \right)\) bằng
2.
6.
8.
4.
Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm \(t\)giây (coi \(t = 0\)là thời điểm viên đạn được bắn lên), vận tốc của nó được cho bởi \(v\left( t \right) = 25 - 9,8t\,\,\left( {{\rm{m/s}}} \right)\). Độ cao của viên đạn (tính từ mặt đất) đạt giá trị lớn nhất là
\(\frac{{125}}{{49}}\).
\(\frac{{3125}}{{98}}\).
\(\frac{{2375}}{{392}}\).
\(\frac{{1125}}{{98}}\).
Nếu \(\int\limits_1^3 f \left( x \right){\rm{d}}x = 2\) thì \[\int\limits_1^3 {\left[ {f\left( x \right) + 2x} \right]dx} \] bằng
\(20\).
\(18\).
\(12\).
\(10\).
Biết \(F\left( x \right) = {x^2}\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\). Giá trị của \(\int\limits_1^2 {\left[ {2 + f\left( x \right)} \right]{\rm{d}}x} \)bằng
\(3\).
\(5\).
\(\frac{{13}}{3}\).
\(\frac{7}{3}\).
Cho \(f\left( x \right) = \left\{ \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x \ge 1\\2x - 1\,\,\,\,{\rm{khi}}\,x < 1\end{array} \right.\). Tính \(J = \int\limits_{ - 1}^2 {f\left( x \right){\rm{d}}x} \).
\( - 1\).
\(\frac{1}{2}\).
\(4\).
\(5\).
Vận tốc của một vật chuyển động là \(v\left( t \right) = 3{t^2} + 5{\rm{ }}\left( {{\rm{m/s}}} \right)\). Quãng đường vật đó đi được từ giây thứ \(4\) đến giây thứ \(10\) là
\(669\) m.
\(696\) m.
\(699\) m.
\(966\) m.
Cho số thực \(a\) và hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x \le 0\\a\left( {x - {x^2}} \right)\,\,\,\,\,{\rm{khi}}\,\,\,x > 0\end{array} \right.\). Tính tích phân \(\int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} \).
\(\frac{a}{6} - 1.\)
\(\frac{{2a}}{3} + 1.\)
\(\frac{a}{6} + 1.\)
\(\frac{{2a}}{3} - 1.\)
Với \(a,b\) là các tham số thực. Giá trị tích phân \(\int\limits_0^b {\left( {3{x^2} - 2ax - 1} \right){\rm{d}}x} \) bằng
\({b^3} - {b^2}a - b\).
\({b^3} + {b^2}a + b\).
\({b^3} - b{a^2} - b\).
\(3{b^2} - 2ab - 1\).
Tính tích phân \(I = \int\limits_1^e {\left( {\frac{1}{x} - \frac{1}{{{x^2}}}} \right)} \,{\rm{d}}x\).
\(I = \frac{1}{e}\).
\(I = \frac{1}{e} + 1\).
\(I = 1\).
\(I = e\).
Biết \(\int\limits_1^3 {\frac{{x + 2}}{x}} \,{\rm{d}}x = a + b\ln c,\) với \(a,b,c \in \mathbb{Z},c < 9.\) Tính tổng \(S = a + b + c.\)
\(S = 7\).
\(S = 5\).
\(S = 8\).
\(S = 6\).
Cho \(\int\limits_1^2 {{e^{3x - 1}}{\rm{d}}x} = m\left( {{e^p} - {e^q}} \right)\) với \(m\), \(p\), \(q \in \mathbb{Q}\) và là các phân số tối giản. Giá trị \(m + p + q\) bằng
\(10\).
\(6\).
\(\frac{{22}}{3}\).
\(8\).
Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\] như vẽ hình bên, trục hoành và hai đường thẳng \[x = a\], \[x = b\]\[\left( {a < b} \right)\] tính theo công thức nào dưới đây?
![Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\] như vẽ hình bên, trục hoành và hai (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid0-1736178868.png)
\(S = \int\limits_a^c {f\left( x \right){\rm{d}}x + \int\limits_c^b {f\left( x \right){\rm{d}}x} } .\)
\[S = \int\limits_a^b {f\left( x \right){\rm{d}}x} .\]
\(S = - \int\limits_a^c {f\left( x \right){\rm{d}}x + \int\limits_c^b {f\left( x \right){\rm{d}}x} } .\)
\[S = - \int\limits_a^b {f\left( x \right){\rm{d}}x} .\]
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 3\), \(x = 2\). Đặt \(a = \int\limits_{ - 3}^1 {f\left( x \right)\,{\rm{d}}x} \), \(b = \int\limits_1^2 {f\left( x \right)\,{\rm{d}}x} \). Mệnh đề nào sau đây là đúng?
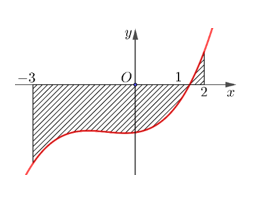
\(S = a + b.\)
\(S = a - b.\)
\(S = - a - b.\)
\(S = b - a.\)
Gọi \(V\) là thể tích khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi các đường \(y = {e^x},\,\,y = 0,\,\,x = 0,\,\,x = 2\) quay quanh \(Ox\). Phát biểu nào sau đây là đúng?
\(V = \pi \int\limits_0^2 {{e^{2x}}} \;{\rm{d}}x\).
\(V = \int\limits_0^2 {{e^x}} \;{\rm{d}}x\).
\(V = \pi \int\limits_0^2 {{e^x}} \;{\rm{d}}x\).
\(V = \int\limits_0^2 {{e^{2x}}} \;{\rm{d}}x\).
Cho hàm số \[y = f\left( x \right)\] có đồ thị \[y = f'\left( x \right)\] cắt trục \[Ox\] tại ba điểm có hoành độ \[a < b < c\] như hình bên.Mệnh đề nào sau đây là đúng?
![Cho hàm số \[y = f\left( x \right)\] có đồ thị \[y = f'\left( x \right)\] cắt trục \[Ox\] tại ba điểm có hoành (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid2-1736179204.png)
\[f\left( c \right) > f\left( a \right) > f\left( b \right)\].
\[f\left( c \right) > f\left( b \right) > f\left( a \right)\].
\[f\left( a \right) > f\left( b \right) > f\left( c \right)\].
\[f\left( b \right) > f\left( a \right) > f\left( c \right)\].
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 4x - {x^2}\), \(y = 2x\)và hai đường thẳng \[x = 1,x = e\]bằng
\(4\).
\(\frac{{20}}{3}\).
\(\frac{4}{3}\).
\(\frac{{16}}{3}\)
Cho hình phẳng giới hạn bởi các đường \[y = \sqrt x - 2\], \[y = 0\] và \[x = 4,x = 9\] quay xung quanh trục \[Ox\]. Thể tích khối tròn xoay tạo thành là
\[V = \frac{7}{6}\].
\[V = \frac{{5\pi }}{6}\].
\[V = \frac{{7\pi }}{{11}}\].
\[V = \frac{{11\pi }}{6}\].
Trường Nguyễn Văn Trỗi muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là \(2,25\)mét, chiều rộng tiếp giáp với mặt đất là \(3\) mét. Giá thuê làm mỗi mét vuông là \(1\,500\,000\) đồng. Vậy số tiền nhà trường phải trả là:
\(33\,750\,000\) đồng.
\(3\,750\,000\) đồng.
\(12\,750\,000\) đồng.
\(6\,750\,000\) đồng.
Cho một viên gạch men có dạng hình vuông \(OABC\) như hình vẽ bên. Sau khi tọa độ hóa, ta có \(O\left( {0\,;\,0} \right)\), \(A\left( {0\,;\,1} \right)\), \(B\left( {1\,;\,1} \right)\), \(C\left( {1\,;\,0} \right)\) và hai đường cong lần lượt là đồ thị hàm số \(y = {x^3}\) và \(y = \sqrt[3]{x}\). Diện tích của phần không được tô đậm trên viên gạch men bằng
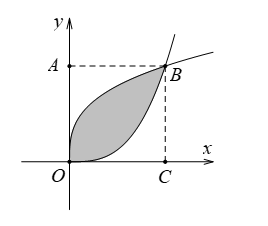
\[\frac{2}{3}\].
\[\frac{3}{4}\].
\[\frac{1}{2}\].
\[\frac{7}{{15}}\].
Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng\[R\]. Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc \[30^\circ \] ta thu được hai khối gỗ có thể tích là \[{V_1}\] và \[{V_2}\], với .
![Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng \[R\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid8-1736179875.png)
Thể tích \[{V_1}\] bằng
\[{V_1} = \frac{{2\sqrt 3 {R^3}}}{9}\].
\[{V_1} = \frac{{\sqrt 3 \pi {R^3}}}{{27}}\].
\[{V_1} = \frac{{\sqrt 3 \pi {R^3}}}{{18}}\].
\[{V_1} = \frac{{\sqrt 3 {R^3}}}{{27}}\].
Trên mặt phẳng tọa độ Oxy, vẽ nửa đường tròn tâm O, bán kính r = 2, nằm phía trên trục Ox. Gọi D là hình phẳng giới hạn bởi nửa đường tròn, trục Ox và hai đường thẳng \(x = - 1,x = 1\). Thể tích khối tròn xoay tạo thành khi quay D quanh trục Ox bằng
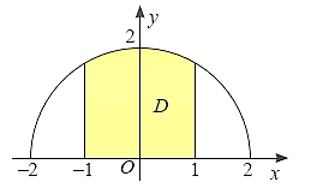
\[\frac{{11\pi }}{3}\].
\[\frac{{22\pi }}{3}\].
\[\frac{{4\pi }}{3}\].
\[\frac{{22}}{3}\].
