5 câu hỏi
Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 - 7t\end{array} \right.\). Đường cao AH có phương trình 2x + 5y + 66 = 0. Khi đó phương trình đường trung trực của cạnh AB có phương trình là:
13x – 3y + 100 = 0;
3x – 13y – 140 = 0;
3x – 13y + 140 = 0;
13x + 3y – 100 = 0.
Cho điểm M nằm trên ∆: x + y – 1 = 0 và cách N(–1; 3) một khoảng bằng 5. Khi đó tọa độ điểm M là:
M(2; –1);
M(–2; –1);
M(–2; 1);
M(2; 1).
Cho đường thẳng ∆: \(\left\{ \begin{array}{l}x = 2 - 3t\\y = 1 + 2t\end{array} \right.\). Hoành độ hình chiếu của điểm M(4; 5) trên ∆ gần nhất với giá trị nào sau đây?
1,1;
1,2;
1,3;
1,5.
Cho hai điểm A(–2; 1), B(3; 5) và đường thẳng d: \(\left\{ \begin{array}{l}x = - 5 + 2t\\y = 9 - 5t\end{array} \right.\). Tọa độ của điểm H ∈ d thỏa mãn \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right|\) đạt giá trị nhỏ nhất là:
\(H\left( { - \frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\);
\(H\left( {\frac{{93}}{{29}}; - \frac{{131}}{{29}}} \right)\);
\(H\left( { - \frac{{93}}{{29}}; - \frac{{131}}{{29}}} \right)\);
\(H\left( {\frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\).
Đường thẳng d trong hình bên biểu thị tổng lít nước được bơm vào một bể nước theo thời gian (đơn vị: giờ).
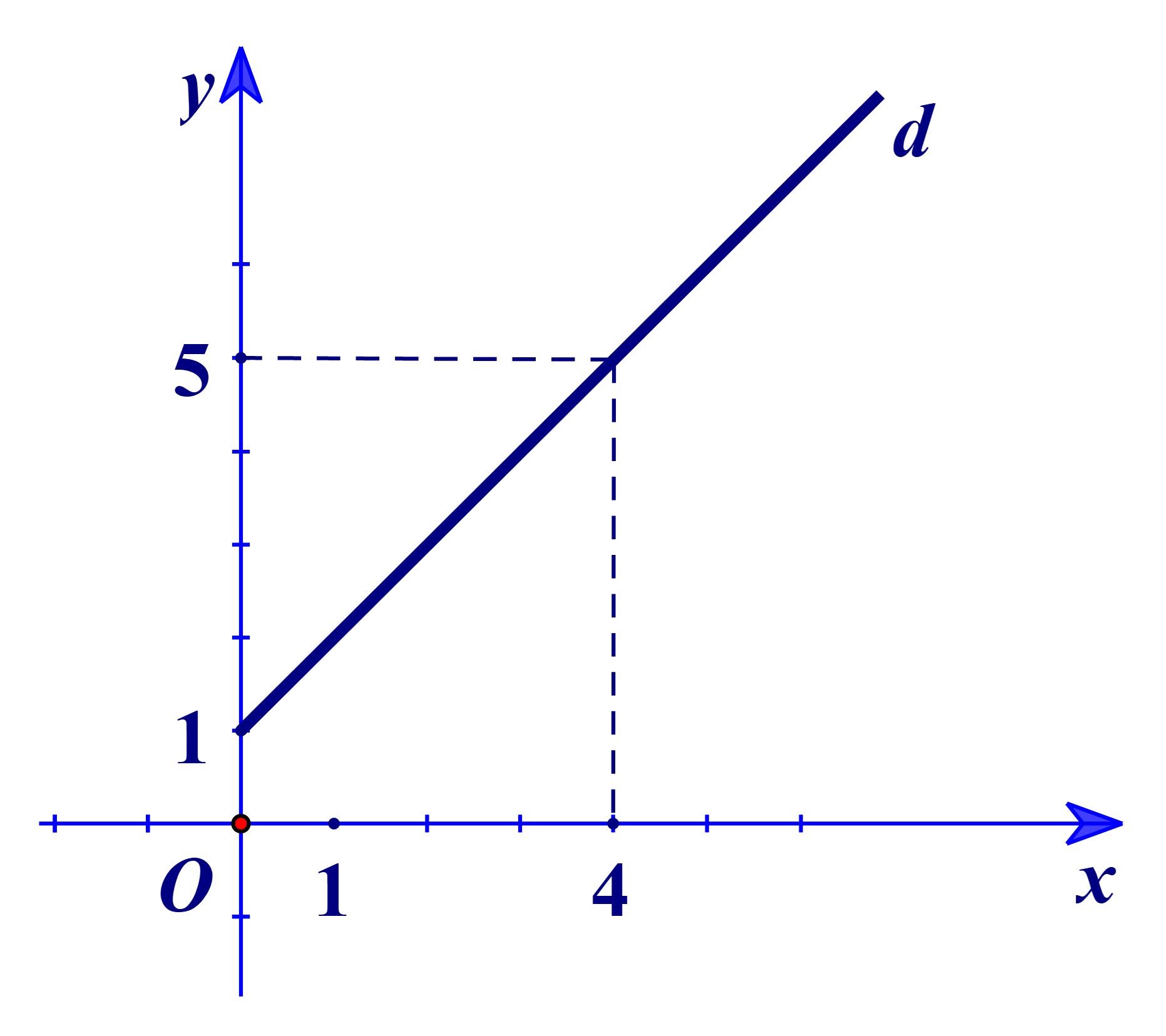
Tổng lít nước mà bể đó chứa sau 15 giờ bằng:
14;
15;
16;
13.
