43 bài tập Phương trình và bất phương trình có lời giải
43 câu hỏi
Phương trình có nghiệm là
\(x = \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{5\pi }}{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{5\pi }}{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{3} + 2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Nghiệm của phương trình \({2^{2x - 4}} = {2^x}\) là
\( - 16\).
\(16\).
\(4\).
\( - 4\).
Nghiệm của phương trình \(\log _3^{}\left( {x - 2} \right) = 2\)là
\(x = 11\).
\(x = 10\).
\(x = 7\).
\(x = 8\).
Giải bất phương trình \({\log _2}\left( {3x - 2} \right) > {\log _2}\left( {6 - 5x} \right)\) được tập nghiệm là \(\left( {a;b} \right)\). Hãy tính tổng \(S = a + b\).
\(S = \frac{{26}}{5}\).
\(S = \frac{{11}}{5}\).
\(S = \frac{{28}}{{15}}\).
\(S = \frac{8}{3}\).
Cho phương trình \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\).
a) Phương trình đã cho tương đương với phương trình \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( {\frac{\pi }{3}} \right)\).
b) Phương trình đã cho có nghiệm là: \(x = \frac{\pi }{4} + k2\pi ;\,\,x = \frac{{7\pi }}{{12}} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\).
c) Phương trình đã cho có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\).
d) Số nghiệm của phương trình đã cho trong khoảng \(\left( { - \pi ;\pi } \right)\) là hai nghiệm.
Cho phương trình \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1\) (*).
a) Điều kiện xác định của phương trình: \(x > 1\).
b) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
c) Gọi \(x = a\) là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
d) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}:2x - y - 8 = 0\) với đường thẳng \({d_2}:y = 0\).
Cho bất phương trình \({4^{{x^2} + 5}} \ge {\left( {\frac{1}{8}} \right)^{x - {x^2}}}\).
a) Ta có: \({4^{{x^2} + 5}} = {2^{2\left( {{x^2} + 5} \right)}};\,\,{\left( {\frac{1}{8}} \right)^{x - {x^2}}} = {2^{ - 3\left( {x - {x^2}} \right)}}.\)
b) Bất phương trình đã cho tương đương với bất phương trình\(2\left( {{x^2} + 5} \right) \ge - 3\left( {x - {x^2}} \right)\).
c) Số nghiệm nguyên của bất phương trình là \(6.\)
d) Tích nghiệm nguyên lớn nhất và nghiệm nguyên nhỏ nhất của bất phương trình là \( - 4.\)
Một cây cầu có dạng cung \(AB\)của đồ thị hàm số \(y = 4,8\cos \frac{x}{9}\) và được mô tả trong hệ trục toạ độ với đơn vị trục là mét như ở hình vẽ dưới đây.
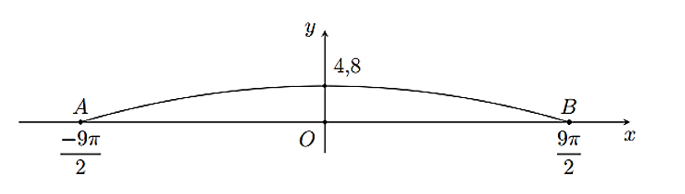
Một sà lan chở khối hàng hoá được xếp thành hình hộp chữ nhật với độ cao \(3,6\,{\rm{m}}\) so với mực nước sông. Hỏi chiều rộng của khối hàng hoá đó lớn nhất là bao nhiêu mét để sà lan có thể đi qua được gầm cầu (làm tròn kết quả đến hàng đơn vị)?
Cô Liên gửi \[100\]triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là \[12\] tháng với lãi suất \(6\% \) một năm. Giả sử qua các năm thì lãi suất không thay đổi và cô Liên không gửi thêm tiền vào mỗi năm. Hỏi sau ít nhất bao nhiêu năm thì số tiền cô Liên có được cả gốc và lãi nhiều hơn \[150\] triệu đồng (làm tròn kết quả đến hàng đơn vị)?
Phương trình \[\sin x = \frac{{\sqrt 3 }}{2}\] có nghiệm là:
\[x = \pm \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{6} + k\pi \] và \[x = \frac{{5\pi }}{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{3} + k2\pi \] và \[x = \frac{{2\pi }}{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Các nghiệm của phương trình \(\sin x = \sin 30^\circ \) là
\(x = 30^\circ + k360^\circ \) và \(x = 150^\circ + k360^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm 30^\circ + k360^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = 30^\circ + k360^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = - 30^\circ + k360^\circ \) và \(x = - 150^\circ + k360^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
Tìm tất cả các nghiệm của phương trình \[\sin \left( {x + \frac{\pi }{6}} \right) = 1\].
\[x = \frac{\pi }{3} + k\pi \]\[\left( {k \in \mathbb{Z}} \right)\].
\[x = - \frac{\pi }{6} + k2\pi \]\[\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{3} + k2\pi \]\[\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{{5\pi }}{6} + k2\pi \]\[\left( {k \in \mathbb{Z}} \right)\].
Nghiệm của phương trình \(\cos \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) là
\(x = k2\pi \) và \(x = - \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = k\pi \) và \(x = - \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\[x = k\pi \,\] và \[x = - \frac{\pi }{2} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\].
\(x = k2\pi \,\,\)và \(x = - \frac{\pi }{2} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\).
Nghiệm của phương trình \(\cos x = - \frac{1}{2}\) là
\(x = \pm \frac{{2\pi }}{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \pm \frac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Nghiệm của phương trình \[\tan 3x = \tan x\] là
\[x = \frac{{k\pi }}{2}\,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{{k\pi }}{6}\,\,\left( {k \in \mathbb{Z}} \right)\].
Phương trình lượng giác \(\sqrt 3 \,\tan \,x + 3 = 0\) có nghiệm là
\[x = \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = - \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = - \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Phương trình \(\tan \left( {3x - 15^\circ } \right) = \sqrt 3 \) có các nghiệm là
\(x = 60^\circ + k180^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = 75^\circ + k180^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = 75^\circ + k60^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = 25^\circ + k60^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
Phương trình \(\sin x = \cos x\) có bao nhiêu nghiệm thuộc đoạn \[\left[ { - \pi ;\pi } \right]\]?
\[3\].
\[5\].
\[2\].
\[4\].
Phương trình lượng giác \(3\cot \,x - \sqrt 3 = 0\) có nghiệm là
\[x = \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Vô nghiệm.
\[x = \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = \frac{\pi }{3} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Giải phương trình \(cot\left( {3x - 1} \right) = - \sqrt 3 \) ta được
\(x = \frac{1}{3} + \frac{{5\pi }}{{18}} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{1}{3} - \frac{\pi }{{18}} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{5\pi }}{{18}} + k\frac{\pi }{3}\,\,\,\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{1}{3} - \frac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) để phương trình \(\cos \left( {2x - \frac{\pi }{3}} \right) - m = 2\) có nghiệm. Tính tổng \(T\) của các phần tử trong \(S.\)
\(T = 6.\)
\(T = 3.\)
\(T = - 2.\)
\(T = - 6.\)
Phương trình \[\sin 2x + \cos x = 0\] có tổng các nghiệm trong khoảng \[\left( {0;\,2\pi } \right)\] bằng
\(2\pi \).
\(3\pi \).
\(5\pi \).
\(6\pi \).
Giải phương trình \[\frac{{\tan x - \sin x}}{{{{\sin }^3}x}} = \frac{1}{{\cos x}}\].
\[x = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
\[x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Vô nghiệm.
\[x = \frac{{k\pi }}{2}\,\,\left( {k \in \mathbb{Z}} \right)\].
Tập nghiệm của bất phương trình \({\left( {\frac{1}{3}} \right)^x} > 9\) trên tập số thực là
\[\left( {2; + \infty } \right)\].
\(\left( { - \infty ; - 2} \right)\).
\(\left( { - \infty ;2} \right)\).
\(\left( { - 2; + \infty } \right)\).
Tập nghiệm của phương trình \({5^{x + 2}} = 1\) là
\(S = \left\{ 3 \right\}\).
\(S = \left\{ 2 \right\}\).
\(S = \left\{ 0 \right\}\).
\(S = \left\{ { - 2} \right\}\).
Tập nghiệm \(S\)của bất phương trình \({\log _5}x > 2\)là
\(S = \left( {32; + \infty } \right)\).
\(S = \left( {25; + \infty } \right)\).
\(S = \left( {10; + \infty } \right)\).
\(S = \left( {\frac{2}{5}; + \infty } \right)\).
Nghiệm của phương trình \({2^{2x - 1}} = 8\) là
\(x = 2\).
\(x = \frac{5}{2}\).
\(x = 1\).
\(x = \frac{3}{2}\).
Nghiệm của phương trình \[{\log _2}\left( {x - 2} \right) = 3\] là
\[x = 6\].
\[x = 8\].
\[x = 11\].
\[x = 10\].
Tổng các nghiệm của phương trình \({2^{{x^2} + 2x}} = {8^{2 - x}}\) bằng
\( - 6\).
\( - 5\).
\(5\).
\(6\).
Số nghiệm của phương trình \[{\log _3}\left( {6 + x} \right) + {\log _3}9x - 5 = 0\] là
\(0\).
\(2\).
\(1\).
\(3\).
Tìm tập nghiệm \(S\) của phương trình \({\log _{\sqrt 2 }}\left( {x - 1} \right) + {\log _{\frac{1}{2}}}\left( {x + 1} \right) = 1\).
\(S = \left\{ 3 \right\}\).
\(S = \left\{ {2 - \sqrt 5 ;2 + \sqrt 5 } \right\}\).
\(S = \left\{ {2 + \sqrt 5 } \right\}\).
\(S = \left\{ {\frac{{3 + \sqrt {13} }}{2}} \right\}\).
Gọi \({x_1},{\rm{ }}{x_2}\) là hai nghiệm của phương trình \({7^{x + 1}} = {\left( {\frac{1}{7}} \right)^{{x^2} - 2x - 3}}\). Khi đó \(x_1^2 + x_2^2\) bằng
\(17\).
\(1\).
\(5\).
\(3\).
Số nghiệm nguyên của bất phương trình \({\left( {\frac{1}{3}} \right)^{2{x^2} - 3x - 7}} > {3^{2x - 21}}\) là
\(7\).
\(6\).
Vô số.
\(8\).
Số nghiệm nguyên của bất phương trình \[{\log _{\frac{\pi }{4}}}\left( {3x + 1} \right) \ge {\log _{\frac{\pi }{4}}}\left( {2x + 5} \right)\]là
\(5\).
\(4\).
\(6\).
vô số.
Tập nghiệm của bất phương trình \({\log _{2 - \sqrt 3 }}\left( {2x - 5} \right) \ge {\log _{2 - \sqrt 3 }}\left( {x - 1} \right)\) là
\(\left( {\frac{5}{2};4} \right]\).
\(\left( {1;\,4} \right]\).
\(\left[ {\frac{5}{2};4} \right]\).
\(\left[ {4; + \infty } \right)\).
Tập nghiệm của bất phương trình \({5^{x - 1}} \ge {5^{{x^2} - x - 9}}\) là
\(\left[ { - 2;4} \right]\).
\(\left[ { - 4;2} \right]\).
\(\left( { - \infty ; - 2} \right] \cup \left[ {4; + \infty } \right)\).
\(\left( { - \infty ; - 4} \right] \cup \left[ {2; + \infty } \right)\).
Tập nghiệm của bất phương trình \({9^x} + 2 \cdot {3^x} - 3 > 0\) là
\(\left[ {0\,; + \infty } \right)\).
\(\left( {0\,; + \infty } \right)\).
\(\left( {1\,; + \infty } \right)\).
\(\left[ {1\,; + \infty } \right)\).
Cho phương trình \(\tan \left( {2x - 15^\circ } \right) = 1\) (*).
a) Phương trình (*) có nghiệm \(x = 30^\circ + k90^\circ \,\,\left( {k \in \mathbb{Z}} \right)\).
b) Phương trình có nghiệm âm lớn nhất bằng \( - 30^\circ \).
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - 180^\circ ;90^\circ } \right)\) bằng \(180^\circ \).
d) Trong khoảng \(\left( { - 180^\circ ;90^\circ } \right)\), phương trình có nghiệm lớn nhất bằng \(60^\circ \).
Cho phương trình \(\sin \left( {2x - \frac{\pi }{4}} \right) = \sin \left( {x + \frac{{3\pi }}{4}} \right)\) (*).
a) Phương trình có nghiệm: \(x = \pi + k2\pi \) và \(x = \frac{\pi }{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
b) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{7\pi }}{6}\).
d) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có nghiệm lớn nhất bằng \(\frac{{5\pi }}{6}\).
Cho phương trình lượng giác \(\cot 3x = - \frac{1}{{\sqrt 3 }}\) (*).
a) Phương trình (*) tương đương \(\cot 3x = \cot \left( {\frac{{ - \pi }}{6}} \right)\).
b) Phương trình (*) có nghiệm \(x = \frac{\pi }{9} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};0} \right)\) bằng \(\frac{{ - 5\pi }}{9}\).
d) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{{2\pi }}{9}\).
Cho hai đồ thị hàm số \(y = \sin \left( {x + \frac{\pi }{4}} \right)\) và \(y = \sin x\).
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: \(\sin \left( {x + \frac{\pi }{4}} \right) = \sin x\).
b) Hoành độ giao điểm của hai đồ thị là \(x = \frac{{3\pi }}{8} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
c) Khi \[x \in \left[ {0;2\pi } \right]\] thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi \(x \in \left[ {0;2\pi } \right]\) thì toạ độ giao điểm của hai đồ thị hàm số là: \(\left( {\frac{{5\pi }}{8};\sin \frac{{5\pi }}{8}} \right),\left( {\frac{{7\pi }}{8};\sin \frac{{7\pi }}{8}} \right)\).
Cho phương trình \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
a) Hạ bậc hai vế, ta được phương trình \(\frac{{1 + \cos \left( {4x + \frac{\pi }{2}} \right)}}{2} = \frac{{1 - \cos \left( {2x + \pi } \right)}}{2}\).
b) Ta có \(\cos \left( {2x + \pi } \right) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = & \frac{\pi }{{12}} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
Một vật dao động xung quanh vị trí cân bằng theo phương trình \(x = 1,5\cos \left( {\frac{{t\pi }}{4}} \right)\); trong đó \(t\) là thời gian được tính bằng giây và quãng đường \(h = \left| x \right|\) được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng (xem hình bên).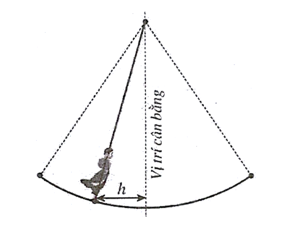
a) Vật ở xa vị trí cân bằng nhất nghĩa là \(h = 1,5\;\,{\rm{m}}\).
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì \(\cos \left( {\frac{{t\pi }}{4}} \right) = 0\).
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
