31 câu hỏi
Gọi \(\alpha \) là góc giữa hai đường thẳng AB, CD. Khẳng định nào sau đây là khẳng định đúng:
\(\cos \alpha = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}}.\)
\(\cos \alpha \,\, = \,\,\frac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}}.\)
\[\cos \alpha \,\, = \,\,\frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {CD} } \right]} \right|}}.\]
\(\cos \alpha \,\, = \,\,\frac{{\left| {\left[ {\overrightarrow {AB} .\overrightarrow {CD} } \right]} \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}}.\)
Cho hai đường thẳng \({d_1}:\,\,\left\{ \begin{array}{l}x\,\, = \,\,2\,\, + \,\,t\\y\,\, = \,\, - 1\,\, + \,\,t\\z\,\, = \,\,3\end{array} \right.\) và \({d_2}:\,\,\left\{ \begin{array}{l}x\,\, = \,\,1\,\, - \,\,t\\y\,\, = \,\,2\\z\,\, = \,\, - 2\,\, + \,\,t\end{array} \right.\). Góc giữa hai đường thẳng d1 và d2 là:
300
1200
1500
600
Cho đường thẳng \(\Delta :\,\,\frac{x}{1}\,\, = \,\,\frac{y}{{ - \,2}}\,\, = \,\,\frac{z}{1}\) và mặt phẳng (P): \(5x\,\, + \,\,11y\,\, + \,\,2z\,\, - \,\,4\,\, = \,\,0\). Góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) là:
600
-300
300
-600
Trong không gian với hệ tọa độ Oxyz cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = 2 + 2t}\\{z = 3 + t}\end{array}} \right.\) và mặt phẳng (P):\(x - y + 3 = 0\). Tính số đo góc giữa đường thẳng d và mặt phẳng (P).
600
300
1200
450
Trong không gian \[Oxyz\], cho mặt phẳng (P): \( - \sqrt 3 x + y + 1 = 0\). Tính góc tạo bởi \[(P)\] với trục \[Ox\]?
600
300
1200
1500
Cho mặt phẳng \((P):\,\,3x\,\, + \,\,4y\,\, + \,\,5z\,\, + \,\,2\,\, = \,\,0\) và đường thẳng d là giao tuyến của hai mặt phẳng \((\alpha ):\,\,x\,\, - \,\,2y\,\, + \,\,1\,\, = \,\,0;\,\,(\beta ):\,\,x\,\, - \,\,2z\,\, - \,\,3\,\, = \,\,0\). Gọi \(\varphi \) là góc giữa đường thẳng d và mặt phẳng (P). Khi đó:
600
450
300
900
Cho mặt phẳng \((\alpha ):\,\,2x\,\, - \,\,y\,\, + \,\,2z\,\, - \,\,1\,\, = \,\,0;\,\,(\beta ):\,\,x\,\, + \,\,2y\,\, - \,\,2z\,\, - \,\,3\,\, = \,\,0\). Cosin góc giữa mặt phẳng \((\alpha )\)và mặt phẳng\(\,(\beta )\) bằng:
\(\frac{4}{9}\)
\( - \frac{4}{9}.\)
\(\frac{4}{{3\sqrt 3 }}.\)
\( - \frac{4}{{3\sqrt 3 }}.\)
Hai mặt phẳng nào dưới đây tạo với nhau một góc 600
\((P):\,\,2x\,\, + \,\,11y\,\, - \,\,5z\,\, + \,\,3 = \,\,0\) và \((Q):\,\,x\,\, + \,\,2y\,\, - \,\,z\,\, - \,\,2 = \,\,0\).
\((P):\,\,2x\,\, + \,\,11y\,\, - \,\,5z\,\, + \,\,3 = \,\,0\) và \((Q):\,\, - x\,\, + \,\,2y\,\, + \,\,z\,\, - \,\,5 = \,\,0\).
\((P):\,\,2x\,\, - \,\,11y\,\, + \,\,5z\,\, - \,\,21 = \,\,0\) và \((Q):\,\,2x\,\, + \,\,y\,\, + \,\,z\,\, - \,\,2 = \,\,0\).
\((P):\,\,2x\,\, - \,\,5y\,\, + \,\,11z\,\, - \,\,6 = \,\,0\) và \((Q):\,\, - x\,\, + \,\,2y\,\, + \,\,z\,\, - \,\,5 = \,\,0\).
Tính tổng các giá trị tham số \(m\) để mặt phẳng \[\left( P \right):\left( {m + 2} \right)x + 2my - mz + 5 = 0\] và \(\left( Q \right):mx + \left( {m - 3} \right)y + 2z - 3 = 0\) hợp với nhau một góc
\(6\)
\(4\)
\(8\)
\( - 4\)
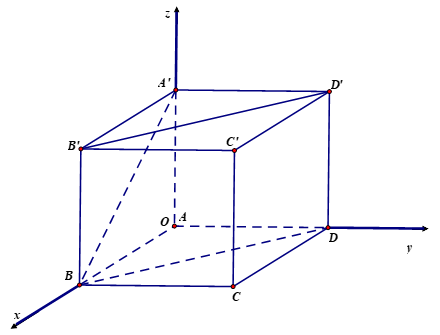
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a,\) gọi \(\alpha \) là góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {BB'D'D} \right).\) Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ, tính \(\sin \alpha \).
\(\frac{{\sqrt 3 }}{5}.\)
\(\frac{{\sqrt 3 }}{2}.\)
\(\frac{1}{2}.\)
\(\frac{{\sqrt 3 }}{4}.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông có độ dài đường chéo bằng \(a\sqrt 2 \) và \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABCD} \right)\). Chọn hệ trục tọa độ \[Oxyz\] như hình vẽ. Nếu \(\tan \alpha = \sqrt 2 \) thì góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBC} \right)\) bằng
300
600
450
900
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], cạnh bên \[SA = 2a\] và vuông góc với mặt phẳng đáy. Gọi \[M\] là trung điểm cạnh \[SD.\] Tính tang của góc tạo bởi hai mặt phẳng \[\left( {AMC} \right)\] và \[\left( {SBC} \right)\] bằng
\[\frac{{\sqrt 3 }}{2}.\]
\[\frac{{2\sqrt 3 }}{3}.\]
\[\frac{{\sqrt 5 }}{5}.\]
\[\frac{{2\sqrt 5 }}{5}.\]
Cho hình chóp \(S.ABCD\) có\(ABCD\) là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(SB\), \(SD\). Côsin của góc hợp bới hai mặt phẳng \(\left( {AEF} \right)\) và \(\left( {ABCD} \right)\) là.
\(\frac{1}{2}\).
\(\frac{{\sqrt 3 }}{3}\).
\(\sqrt 3 \).
\(\frac{{\sqrt 3 }}{2}\).
Cho hình chóp \[O.ABC\] có ba cạnh \[OA\], \[OB\], \[OC\] đôi một vuông góc và \[OA = OB = OC = a\]. Gọi \[M\] là trung điểm cạnh \[AB\]. Góc tạo bởi hai vectơ \[\overrightarrow {BC} \] và \[\overrightarrow {OM} \] bằng
1350
1500
1200
600
Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), \[SA = a\sqrt 2 \]. Gọi \(G\) là trọng tâm tam giác \(SCD\). Góc giữa đường thẳng \(BG\) với đường thẳng \(SA\) bằng:
\(\arccos \frac{{\sqrt 3 }}{5}\).
\(\arccos \frac{{\sqrt 5 }}{5}\).
\(\arccos \frac{{\sqrt 5 }}{3}\).
\[\arccos \frac{{\sqrt {15} }}{5}\].
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi, tam giác \[ABD\] đều. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(BC\) và \(C'D'\), biết rằng \(MN \bot B'D\). Gọi \(\alpha \) là góc tạo bởi đường thẳng \(MN\) và mặt đáy \(\left( {ABCD} \right)\), khi đó \(\cos \alpha \) bằng:
\(\cos \alpha = \frac{1}{{\sqrt 3 }}\).
\(\cos \alpha = \frac{{\sqrt 3 }}{2}\).
\(\cos \alpha = \frac{1}{{\sqrt {10} }}\).
\(\cos \alpha = \frac{1}{2}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SAB\) là tam giác đều và \(\left( {SAB} \right)\) vuông góc với \(\left( {ABCD} \right)\). Tính \(\cos \varphi \) với \(\varphi \) là góc tạp bởi \(\left( {SAC} \right)\) và \(\left( {SCD} \right)\).
\[\frac{{\sqrt 3 }}{7}\].
\[\frac{{\sqrt 6 }}{7}\].
\[\frac{5}{7}\].
\[\frac{{\sqrt 2 }}{7}\].
Cho hình lập phương \(ABC{\rm{D}}.A'B'C'D'\)có cạnh a. Góc giữa hai mặt phẳng \(\left( {A'B'CD} \right)\) và \(\left( {ACC'A'} \right)\) bằng
600
300
450
750
Cho hình chóp tứ giác đều \(S.ABCD\)có đáy \(ABCD\) là hình vuông cạnh \(a\), tâm \(O\). Gọi \(M\) và \(N\) lần lượt là trung điểm của hai cạnh \(SA\) và \(BC\), biết \(MN = \frac{{a\sqrt 6 }}{2}\). Khi đó giá trị sin của góc giữa đường thẳng \(MN\) và mặt phẳng \[\left( {SBD} \right)\] bằng
\[\frac{{\sqrt 2 }}{5}\].
\[\frac{{\sqrt 3 }}{3}\].
\[\frac{{\sqrt 5 }}{5}\].
\[\sqrt 3 \].
Cho hình lăng trụ \[ABC.A'B'C'\] có \[A'.ABC\] là tứ diện đều cạnh \[a\]. Gọi \[M\], \[N\] lần lượt là trung điểm của \[AA'\] và \[BB'\]. Tính tan của góc giữa hai mặt phẳng \[\left( {ABC} \right)\] và \[\left( {CMN} \right)\].
\(\frac{{\sqrt 2 }}{5}\).
\(\frac{{3\sqrt 2 }}{4}\).
\(\frac{{2\sqrt 2 }}{5}\).
\(\frac{{4\sqrt 2 }}{{13}}\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[2a\], cạnh bên \[SA = a\] và vuông góc với mặt phẳng đáy. Gọi \[M\] là trung điểm cạnh \[SD\]. Tan của góc tạo bởi hai mặt phẳng \[\left( {AMC} \right)\]và \[\left( {SBC} \right)\] bằng
\(\frac{{\sqrt 5 }}{5}\).
\(\frac{{2\sqrt 5 }}{5}\).
\(\frac{{\sqrt 3 }}{2}\).
\(\frac{{2\sqrt 3 }}{3}\).
Cho hình chóp \(S.ABCD\) đáy là hình thang vuông tại \(A\) và \(B\), \(AB = BC = a,{\rm{ }}AD = 2a\). Biết \(SA \bot (ABCD),{\rm{ }}SA = a\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(SB\) và \(CD\). Tính sin góc giữa đường thẳng \(MN\) và mặt phẳng \((SAC)\).
\(\frac{{3\sqrt 5 }}{{10}}.\)
\(\frac{{2\sqrt 5 }}{5}.\)
\(\frac{{\sqrt 5 }}{5}.\)
\(\frac{{\sqrt {55} }}{{10}}.\)
Cho hình chóp tứ giác đều \[S.ABCD\] có cạnh đáy bằng \[a\], tâm \[O\]. Gọi \[M\] và \[N\] lần lượt là trung điểm của \[SA\] và \[BC\]. Biết rằng góc giữa \[MN\] và \[\left( {ABCD} \right)\] bằng \(60^\circ \), côsin của góc giữa đường thẳng \[MN\] và mặt phẳng \[\left( {SBD} \right)\] bằng:
\(\frac{{\sqrt 5 }}{5}\).\[\]
\(\frac{{\sqrt {41} }}{{41}}\).
\(\frac{{2\sqrt 5 }}{5}\).
\(\frac{{2\sqrt {41} }}{{41}}\).
Cho hình chóp \(S.ABCD\) có đáy hình vuông. Cho tam giác \(SAB\) vuông tại \(S\) và góc \(SBA\) bằng 300 . Mặt phẳng \(\left( {SAB} \right)\) vuông góc mặt phẳng đáy. Gọi \(M,N\) là trung điểm \(AB,BC\). Tìm cosin góc tạo bởi hai đường thẳng \(\left( {SM,DN} \right)\).
\(\frac{2}{{\sqrt 5 }}\).
\(\frac{1}{{\sqrt 5 }}\).
\(\frac{1}{{\sqrt 3 }}\).
\(\frac{{\sqrt 2 }}{{\sqrt 3 }}\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], cạnh bên \[SA\] vuông góc với mặt phẳng đáy, \[SA = a\sqrt 2 \]. Gọi \[M\], \[N\] lần lượt là hình chiếu vuông góc của điểm \[A\] trên các cạnh \[SB\], \[SD\]. Góc giữa mặt phẳng \[\left( {AMN} \right)\] và đường thẳng \[SB\] bằng
450
900
1200
600
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a\), \(BC = a\sqrt 3 \), \[SA = a\] và \(SA\) vuông góc với đáy \(ABCD\). Tính \[\sin \alpha \], với \(\alpha \) là góc tạo bởi giữa đường thẳng \(BD\) và mặt phẳng \(\left( {SBC} \right)\).
\[\sin \alpha = \frac{{\sqrt 7 }}{8}\].
\[\sin \alpha = \frac{{\sqrt 3 }}{2}\].
\[\sin \alpha = \frac{{\sqrt 2 }}{4}\].
\[\sin \alpha = \frac{{\sqrt 3 }}{5}\].
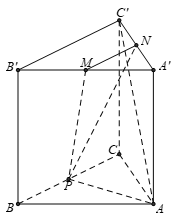
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = 2\sqrt 3 \) và \(AA' = 2.\) Gọi \(M,\,N,\,P\) lần lượt là trung điểm các cạnh \(A'B',\,A'C'\) và \(BC\) (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {MNP} \right)\) bằng
\(\frac{{17\sqrt {13} }}{{65}}\)
\(\frac{{18\sqrt {13} }}{{65}}\)
\(\frac{{6\sqrt {13} }}{{65}}\)
\(\frac{{\sqrt {13} }}{{65}}\)
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có \(AB = AC = a\), góc , \(AA' = a\). Gọi \[M\], \[N\] lần lượt là trung điểm của \(B'C'\) và \(CC'\). Số đo góc giữa mặt phẳng\(\left( {AMN} \right)\) và mặt phẳng \(\left( {ABC} \right)\) bằng
600
300
\[\arcsin \frac{{\sqrt 3 }}{4}\].
\[\arccos \frac{{\sqrt 3 }}{4}\].
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], cạnh bên \[SA = 2a\] và vuông góc với mặt phẳng đáy. Gọi \[M\] là trung điểm cạnh \[SD\]. Tang của góc tạo bởi hai mặt phẳng \[\left( {AMC} \right)\] và \[\left( {SBC} \right)\] bằng
\[\frac{{\sqrt 5 }}{5}\].
\[\frac{{\sqrt 3 }}{2}\].
\[\frac{{2\sqrt 5 }}{5}\].
\[\frac{{2\sqrt 3 }}{3}\].
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(G\) là trọng tâm của tam giác \(SAB\) và \(M,\,N\) lần lượt là trung điểm của \(SC,\,SD\)(tham khảo hình vẽ bên). Tính côsin của góc giữa hai mặt phẳng \(\left( {GMN} \right)\) và \(\left( {ABCD} \right)\).
\(\frac{{2\sqrt {39} }}{{39}}\).
\(\frac{{\sqrt 3 }}{6}\).
\(\frac{{2\sqrt {39} }}{{13}}\).
\(\frac{{\sqrt {13} }}{{13}}\).
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác cân với \(AB = AC = a\) và góc và cạnh bên \(BB' = a\). Gọi \(I\) là trung điểm của \(CC'\). Tính cosin góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\).
\(\frac{{\sqrt 3 }}{{10}}\).
\(\frac{{\sqrt {30} }}{{10}}\).
\(\frac{{\sqrt {30} }}{{30}}\).
\(\frac{{\sqrt {10} }}{{30}}\).
