30 câu Trắc nghiệm Toán 10 Kết nối tri thức Bài tập cuối chương 6 có đáp án
30 câu hỏi
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
\[\emptyset \];
ℝ;
ℝ\{1};
ℝ\{0; 1}.
Cho hàm số có đồ thị như hình vẽ

Kết luận nào sau đây là đúng
Hàm số nghịch biến trên khoảng (– ∞; – 1);
Hàm số đồng biến trên khoảng (1; + ∞);
Hàm số đồng biến trên khoảng (– ∞; 1);
Hàm số nghịch biến trên khoảng (– 1; + ∞).
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
I(– 4; – 4);
I(– 1; – 1);
I(– 4; 4);
I(4; 4).
Đồ thị hàm số y = – 9x2 + 6x – 1 có dạng là:
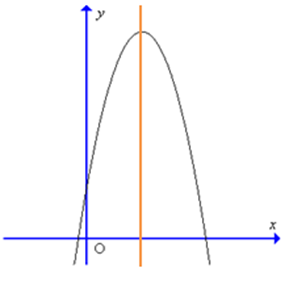
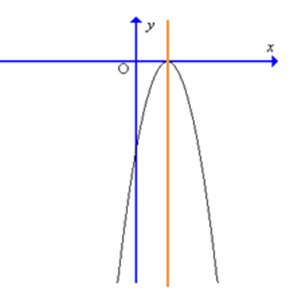
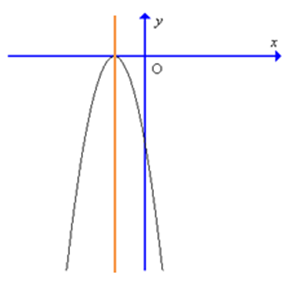
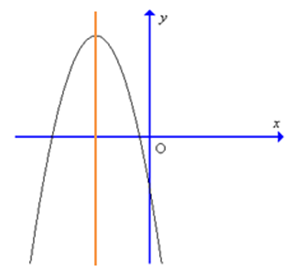
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
f(x) < 0 khi x ∈(– 1; 1);
f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞)
f(x) = 0 khi x = 1; x = – 1;
f(x) > 0 khi x ∈ (– 1; 1);
Tam thức f(x) = x2 – 2x – 3 nhận giá trị dương khi và chỉ khi
x ∈ (– ∞; – 3) \( \cup \) (– 1; + ∞);
x ∈ (– ∞; – 1) \( \cup \) (3; + ∞);
x ∈ (– ∞; – 2) \( \cup \) (6; + ∞);
x ∈ (1; 3).
Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).
y = x2 + 2x + 1;
y = 5x2 – 2x + 1;
y = – x2 + 5x + 1;
y = 2x2 + x + 1.
Nghiệm của phương trình \[\sqrt {2x - 3} = x - 3\]
5;
– 3;
6;
4.
Số nghiệm của phương trình \[\sqrt {{x^2} - 3x} = \sqrt {2x - 4} \]
4;
2;
0;
1.
Tập xác định của hàm số \[y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\] là:
D = [2; + ∞);
D = [2; 6) \[ \cup \] (6; + ∞)
D = (6; + ∞);
D = ℝ\{6}.
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
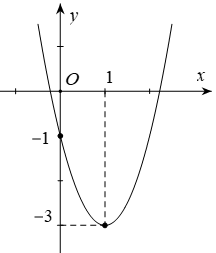
y = 2x2 – 4x – 1;
y = x2 – 2x – 1;
y = 2x2 – 8x – 1;
y = 2x2 – x – 1.
Cho hàm số: y = x2 – 2x – 1, khẳng định nào sau đây sai?
Hàm số đồng biến trên (1; + ∞) ;
Đồ thị hàm số có trục đối xứng x = – 2;
Hàm số nghịch biến trên (– ∞; 1);
Đồ thị hàm số có đỉnh I(1; – 2).
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ℝ.
m < – 1;
m < 0;
– 1 < m < 0.
m < 1 và m ≠ 0.
Tổng các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
1;
0;
2;
\[2\sqrt 2 \].
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] là
x = 2;
x = 4;
x = 5;
x = 6.
Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
(– ∞; + ∞);
(– ∞; 1);
(1; + ∞);
(– ∞; 2).
Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?
m ≥ – 11;
m > – 11;
m < – 11;
m < 11.
Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x2 + 2) là:
\[(--\infty ;1] \cup [4; + \infty )\];
\(\left[ {1;4} \right]\);
\[(--\infty ;1) \cup (4; + \infty )\];
\((1;4)\).
Bất phương trình: \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\] có bao nhiêu nghiệm nguyên dương?
0;
1;
2;
3.
Cho hàm số y = f(x) có đồ thị như hình sau:
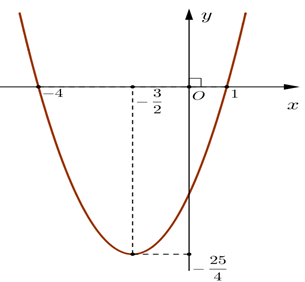
Hàm số đồng biến trên khoảng
\[\left( {--\infty {\rm{;}}--\frac{3}{2}} \right)\];
\[\left( {--\infty {\rm{;}}--\frac{{25}}{4}} \right)\];
\[\left( {--\frac{3}{2}; + \infty } \right)\];
\[\left( {--\frac{{{\rm{25}}}}{{\rm{4}}}; + \infty } \right)\].
Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\)
a = 0;
a < 0;
\(0 < a \le \frac{1}{2}\).
\(a \ge \frac{1}{2}\).
Để f(x) = x2 + (m + 1)x +2m + 7 > 0 với mọi x thì
– 3 ≤ m ≤ 9;
\(\left[ \begin{array}{l}m < - 3\\m > 9\end{array} \right.\).
– 3 < m < 9;
\(\left[ \begin{array}{l}m \le - 3\\m \ge 9\end{array} \right.\).
Tìmtất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
\[\left[ \begin{array}{l}m \le - 22\\m \ge 2\end{array} \right.\];
– 22 ≤ m ≤ 2;
– 22 < m < 2;
\[\left[ \begin{array}{l} - 22 \le m \le 2\\m = 3\end{array} \right.\].
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
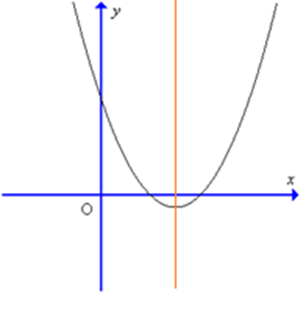
Kết luận nào sau đây đúng về hệ số a, b:
a > 0; b > 0;
a < 0; b > 0;
a > 0; b < 0;
a > 0; c <0.
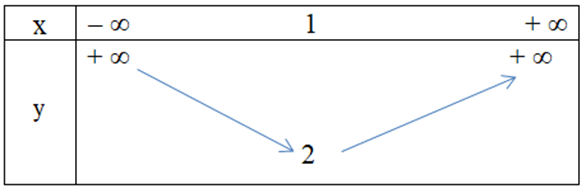
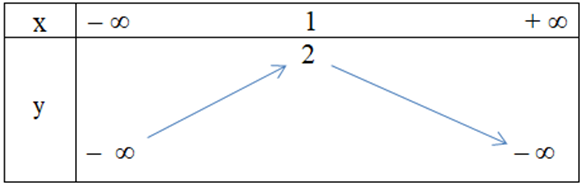
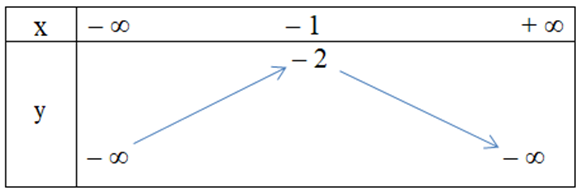
Hàm số y = x2 + 2x – 1 có bảng biến thiên là
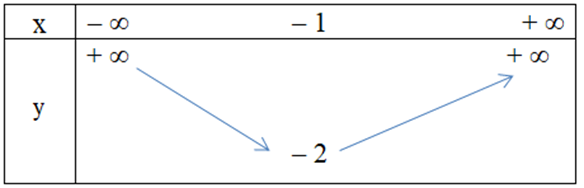
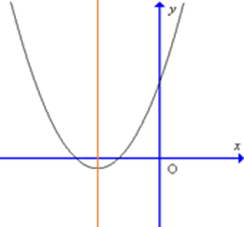
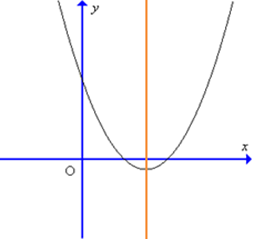
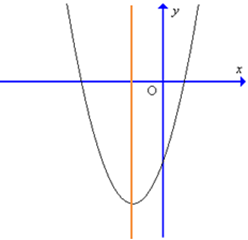
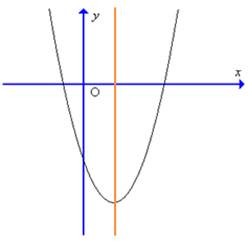
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
Tập xác định của hàm số \[y = \sqrt {x - 2} + \frac{{\sqrt {{x^2} - 1} }}{3}\] là
[2; +∞);
[1; +∞);
\[\left( { - \infty ;1} \right] \cup \left[ {2; + \infty } \right)\];
\[\left( {1;2} \right) \cup \left( {3; + \infty } \right)\].
Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
m < 3;
m < 1;
m = 1;
1 < m < 2.
Số giá trị nguyên của x thỏa mãn điều kiện xác định của phương trình :\(\sqrt {2 - x} + \frac{4}{{\sqrt {x + 1} + 3}} = 1\) là:
0;
1;
2;
3.
Phương trình \[(x + 4)(x + 1) - 3\sqrt {{x^2} + 5x + 2} = 6\] có bao nhiêu nghiệm nguyên âm:
0;
1;
2;
3;
