Quiz

30 câu Trắc nghiệm Toán 10 chân trời sáng tạo Bài tập cuối chương IX có đáp án

VietJackToánLớp 1023 lượt thi

Bắt đầu ngay

30 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm

Trong mặt phẳng Oxy, cho ∆ABC có A(–4; 1), B(2; 4), C(2; –2). Tọa độ trọng tâm I của ∆ABC là:

I(1; 0);

I(0; 1);

I(–1; 0);

I(0; –1).

Xem đáp án

2. Trắc nghiệm

• 1 điểm

Cho $\vec{u} = (4; 5)$ và $\vec{v} = (3; a)$ . Tìm a để $\vec{u} ⊥ \vec{v}$

$a = \frac{12}{5}$

$a = - \frac{12}{5}$

$a = \frac{5}{12}$

$a = - \frac{5}{12}$

Xem đáp án

3. Trắc nghiệm

• 1 điểm

Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:

(3; –2);

(5; 0);

(3; 0);

(5; –2).

Xem đáp án

4. Trắc nghiệm

• 1 điểm

Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng là:

x ∈∅;

x = 1;

x = 11;

x = 11 hoặc x = 1.

Xem đáp án

5. Trắc nghiệm

• 1 điểm

Cho $\vec{a} = (1; 2), \vec{b} = (- 2; 3)$ . Góc giữa hai vectơ $\vec{u} = 3 \vec{a} + 2 \vec{b}$ và $\vec{v} = \vec{a} - 5 \vec{b}$ bằng

45°;

60°;

90°;

135°.

Xem đáp án

6. Trắc nghiệm

• 1 điểm

Trong mặt phẳng Oxy, cho ∆ABC có A(–3; 0), B(3; 0) và C(2; 6). Gọi H(a; b) là trực tâm của ∆ABC. Giá trị của a + 6b bằng:

Xem đáp án

7. Trắc nghiệm

• 1 điểm

Trong mặt phẳng với hệ tọa độ Oxy, cho ∆ABC có A(3; 5), B(9; 7), C(11; –1). Gọi M, N lần lượt là trung điểm của AB và AC. Tọa độ của $\vec{M N}$ là:

(2; –8);

(1; –4);

(10; 6);

(5; 3).

Xem đáp án

8. Trắc nghiệm

• 1 điểm

Cho ∆ABC có A(2; –1), B(4; 5), C(–3; 2). Phương trình tổng quát của đường trung tuyến AM là:

x + 3y – 7 = 0;

3x + y – 7 = 0;

3x + y – 5 = 0;

x + 3y – 5 = 0.

Xem đáp án

9. Trắc nghiệm

• 1 điểm

Giao điểm M của hai đường thẳng (d): ${\begin{cases} x = 1 - 2 t \\ y = - 3 + 5 t \end{cases}$ và (d’): 3x – 2y – 1 = 0 là:

$M (0; \frac{1}{2})$

$M (0; - \frac{1}{2})$

$M (- \frac{1}{2}; 0)$

$M (2; - \frac{11}{2})$

Xem đáp án

10. Trắc nghiệm

• 1 điểm

Cặp đường thẳng nào sau đây vuông góc với nhau?

$d_{1} : {\begin{cases} x = t \\ y = - 1 - 2 t \end{cases}$ và d₂: 2x + y – 1 = 0;

d₁: x – 2 = 0 và $d_{2} : {\begin{cases} x = t \\ y = 0 \end{cases}$

d₁: 2x – y + 3 = 0 và d₂: x – 2y + 1 = 0;

d₁: 2x – y + 3 = 0 và d₂: 4x – 2y + 1 = 0.

Xem đáp án

11. Trắc nghiệm

• 1 điểm

Cho đường thẳng (d): x – 2y + 5 = 0. Mệnh đề nào sau đây đúng?

(d) có hệ số góc k = 1/2;

(d) cắt (d’): x – 2y = 0;

(d) đi qua A(1; –2);

(d) có phương trình tham số: ${\begin{cases} x = t \\ y = - 2 t \end{cases}$ .

Xem đáp án

12. Trắc nghiệm

• 1 điểm

Cho ∆ABC có C(–1; 2), đường cao BH: x – y + 2 = 0, đường phân giác trong AN: 2x – y + 5 = 0. Tọa độ điểm A là:

$A (\frac{- 4}{3}; \frac{7}{3})$

$A (\frac{- 4}{3}; \frac{- 7}{3})$

$A (\frac{4}{3}; \frac{- 7}{3})$

$A (\frac{4}{3}; \frac{7}{3})$

Xem đáp án

13. Trắc nghiệm

• 1 điểm

Trong mặt phẳng Oxy, cho $\vec{a} = (1; 2) v à \vec{b} = (- 1; 3)$ và . Tìm tọa độ sao cho $2 \vec{c} + \vec{a} - 3 \vec{b} = \vec{0}$

$\vec{c} = (- 2; - \frac{7}{2})$

$\vec{c} = (2; \frac{7}{2})$

$\vec{c} = (- 2; \frac{7}{2})$

$\vec{c} = (- 1; \frac{9}{2})$

Xem đáp án

14. Trắc nghiệm

• 1 điểm

Trong mặt phẳng Oxy, cho hai điểm A(2; 4) và B(–2; 10). Giá trị k để điểm D(k; k + 1) thuộc đường thẳng AB là:

k = 2;

k = 7/5

k = 3;

k = 12/5

Xem đáp án

15. Trắc nghiệm

• 1 điểm

Trong mặt phẳng Oxy, cho đường thẳng d: x + 2y – 3 = 0 và hai điểm A(–1; 2). B(2; 1). Điểm C thuộc đường thẳng d sao cho diện tích ∆ABC bằng 2. Tọa độ điểm C là:

C(–9; 6);

C(6; 9);

C(7; –2);

Cả A, C đều đúng.

Xem đáp án

16. Trắc nghiệm

• 1 điểm

Đường thẳng ∆ đi qua giao điểm của hai đường thẳng d₁: 2x + y – 3 = 0 và d₂: x – 2y + 1 = 0, đồng thời tạo với d₃: y – 1 = 0 một góc $\frac{π}{4} .$ Phương trình đường thẳng ∆ là:

2x + y = 0; x – y – 1 = 0;

x + 2y = 0; x – 4y = 0;

x – y = 0; x + y – 2 = 0;

2x + 1 = 0; x – 3y = 0.

Xem đáp án

17. Trắc nghiệm

• 1 điểm

Tọa độ tâm I và bán kính R của đường tròn (C): (x + 1)² + y² = 8 là:

I(–1; 0), R = 8;

I(–1; 0), R = 64;

I(–1; 0), R = $2 \sqrt{2}$ ;

I(1; 0), R = $2 \sqrt{2}$ .

Xem đáp án

18. Trắc nghiệm

• 1 điểm

Tọa độ tâm I và bán kính R của đường tròn (C): 2x² + 2y² – 8x + 4y – 1 = 0 là:

I(–2; 1), R = $\frac{\sqrt{21}}{2}$ ;

I(2; –1), R = $\frac{\sqrt{22}}{2}$ ;

I(4; –2), R = $\sqrt{21}$ ;

I(–4; 2), R = $\sqrt{19}$ .

Xem đáp án

19. Trắc nghiệm

• 1 điểm

Đường tròn (C) có tâm I(–2; 3) và đi qua điểm M(2; –3) có phương trình là:

(x + 2)² + (y – 3)² = $\sqrt{52}$ ;

(x – 2)² + (y + 3)² = 52;

x² + y² + 4x – 6y – 57 = 0;

x² + y² + 4x – 6y – 39 = 0.

Xem đáp án

20. Trắc nghiệm

• 1 điểm

Cho phương trình x² + y² – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:

m ∈ ℝ;

$m \in (- \infty; 1) \cup (2; + \infty)$

$m \in (- \infty; 1] \cup [2; + \infty)$

$m \in (- \infty; \frac{1}{3}) \cup (2; + \infty)$

Xem đáp án

21. Trắc nghiệm

• 1 điểm

Đường tròn (C) có tâm I thuộc đường thẳng d: x + 3y + 8 = 0, đi qua điểm A(–2; 1) và tiếp xúc với đường thẳng ∆: 3x – 4y + 10 = 0. Phương trình đường tròn (C) là:

(x – 2)² + (y + 2)² = 25;

(x + 5)² + (y + 1)² = 16;

(x + 2)² + (y + 2)² = 9;

(x – 1)² + (y + 3)² = 25.

Xem đáp án

22. Trắc nghiệm

• 1 điểm

Tọa độ tâm I của đường tròn đi qua ba điểm A(0; 4), B(2; 4), C(4; 0) là:

I(0; 0);

I(1; 0);

I(3; 2);

I(1; 1).

Xem đáp án

23. Trắc nghiệm

• 1 điểm

Cho đường tròn (C): x² + y² + 4x + 4y – 17 = 0, biết tiếp tuyến của (C) song song với đường thẳng d: 3x – 4y – 2023 = 0. Phương trình tiếp tuyến của đường tròn (C) là:

3x – 4y + 23 = 0; 3x – 4y – 27 = 0;

3x – 4y + 23 = 0; 3x – 4y + 27 = 0;

3x – 4y – 23 = 0; 3x – 4y + 27 = 0;

3x – 4y – 23 = 0; 3x – 4y – 27 = 0.

Xem đáp án

24. Trắc nghiệm

• 1 điểm

Cho đường tròn (C): (x – 2)² + (y + 4)² = 25, biết tiếp tuyến vuông góc với đường thẳng d: 3x – 4y + 5 = 0. Phương trình tiếp tuyến của (C) là:

4x – 3y + 5 = 0; 4x – 3y – 45 = 0;

4x + 3y + 5 = 0; 4x + 3y + 3 = 0;

4x + 3y + 29 = 0;

4x + 3y + 29 = 0; 4x + 3y – 21 = 0.

Xem đáp án

25. Trắc nghiệm

• 1 điểm

Cho đường tròn (C): x² + y² – 2x – 4y + 1 = 0. Gọi d₁, d₂ lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d₁ và d₂ là:

(3; 0);

(–3; 0);

(0; 3);

(0; –3).

Xem đáp án

26. Trắc nghiệm

• 1 điểm

Một trạm viễn thông A được xây tại điểm có tọa độ (2; 3) (trong mặt phẳng Oxy). Một người đang ngồi trên xe hơi chạy trên đường quốc lộ có dạng một đường thẳng ∆ có phương trình x – 5y + 6 = 0.

Một trạm viễn thông A được xây tại điểm có tọa độ (2; 3) (trong mặt phẳng Oxy). Một người đang ngồi trên xe hơi chạy trên đường quốc lộ có dạng một đường thẳng ∆ có phương trình x – 5y + 6 = 0. Biết rằng mỗi đơn vị độ dài tương ứng với 1 km. Khoảng cách ngắn nhất giữa người đó và trạm viễn thông A bằng: (ảnh 1)

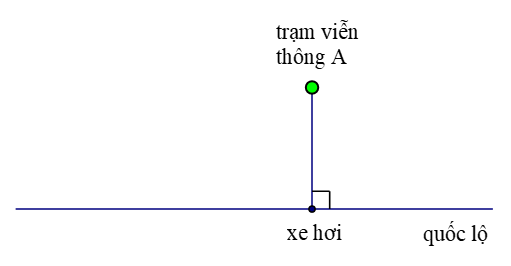
Biết rằng mỗi đơn vị độ dài tương ứng với 1 km. Khoảng cách ngắn nhất giữa người đó và trạm viễn thông A bằng:

2,5 km;

0,2 km;

1,37 km;

0,5 km.

Xem đáp án

27. Trắc nghiệm

• 1 điểm

Cho M(x; y) nằm trên elip (E): $\frac{x^{2}}{121} + \frac{y^{2}}{81} = 1$ . Tỉ số giữa tiêu cự và độ dài trục lớn bằng:

$\frac{11 \sqrt{10}}{20}$

$\frac{2 \sqrt{10}}{9}$

$\frac{2 \sqrt{10}}{11}$

$\frac{9 \sqrt{10}}{20}$

Xem đáp án

28. Trắc nghiệm

• 1 điểm

Một gương có mặt cắt là một hypebol có phương trình $\frac{x^{2}}{144} - \frac{y^{2}}{16} = 1$ được dùng để chụp ảnh toàn cảnh. Máy ảnh hướng về phía đỉnh của gương và được đặt ở vị trí sao cho ống kính trùng với một tiêu điểm của gương như hình vẽ.

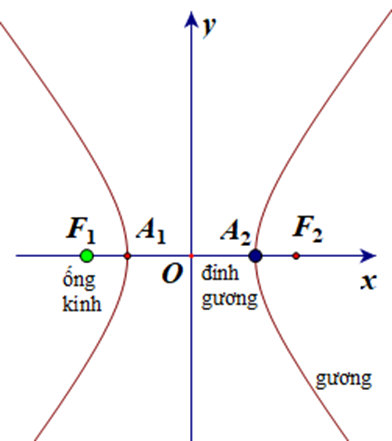
Một gương có mặt cắt là một hypebol có phương trình x^2/144 - y^2/16 = 1 được dùng để chụp ảnh toàn cảnh. Máy ảnh hướng về phía đỉnh của gương và được đặt ở vị trí sao cho ống kính trùng với một tiêu điểm của gương như hình vẽ. (ảnh 1)

Biết rằng x, y được đo theo inch. Khoảng cách từ ống kính tới đỉnh gương bằng khoảng:

24,6 inch;

0,7 inch;

12 inch;

23,3 inch.

Xem đáp án

29. Trắc nghiệm

• 1 điểm

Một tòa tháp có mặt cắt hình hypebol có phương trình $\frac{x^{2}}{36} - \frac{y^{2}}{49} = 1$ . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp bằng:

43,28 m;

22,25 m;

28,31 m;

57,91 m.

Xem đáp án

30. Trắc nghiệm

• 1 điểm

Một anten gương đơn hình parabol có phương trình y² = 20x. Ống thu của anten được đặt tại tiêu điểm của nó. Ta sẽ đặt ống thu tại điểm có tọa độ là:

(0; 10);

(0 ; 5);

(10; 0);

(5; 0).